Cycling City

好不容易切一道$\ast 3100$，写篇题解纪念一下。

Cycling City

考虑什么时候两个点之间有三条完全不重复的路径，当且仅当这两个点在环的交接点的两端。

注意原图不是连通的，以下只考虑连通的情况，不连通的就是从树变成森林。

大概就是这样的,如图，$2,4$就是一个可行的，合法路径分别为$2,3,42,1,5,42,6,7,4$

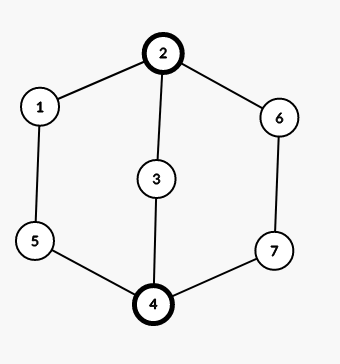
先随意以一个为根，提出一棵树，然后将非树边依次加入，对于每条路径，记录路过其的环，这个暴力跳即可，复杂度是$O(n)$的，因为找到了被覆盖两次的就输出了。如果有一条路径路过的环有两个，那么就一直向上跳，找到另一端，然后统计路径即可。

树上的路径暴力跳树，环上的路径新开一个vector记录一下，输出路径即可。

点此查看代码

#include<bits/stdc++.h>
#include<bits/extc++.h>
// using namespace __gnu_pbds;
// using namespace __gnu_cxx;
using namespace std;
#define infile(x) freopen(x,"r",stdin)
#define outfile(x) freopen(x,"w",stdout)
#define errfile(x) freopen(x,"w",stderr)
#define rep(i,s,t,p) for(int i = s;i <= t; i += p)
#define drep(i,s,t,p) for(int i = s;i >= t; i -= p)
#ifdef LOCAL
    FILE *InFile = infile("in.in"),*OutFile = outfile("out.out");
    // FILE *ErrFile=errfile("err.err");
#else
    FILE *Infile = stdin,*OutFile = stdout;
    //FILE *ErrFile = stderr;
#endif
using ll=long long;using ull=unsigned long long;
using db = double;using ldb = long double;
const int N = 2e5 + 10;
vector<int> have[N];
struct node{int to,id;node(int t,int i):to(t),id(i){}};
vector<node> edge[N];
#define eb emplace_back
#define add(u,v,i) edge[u].eb(node(v,i))
#define All(x) x.begin(),x.end()
int n,m,u[N],v[N],fa[N],e_tof[N],dep[N],tim;
vector<int> ring[N];
bitset<N> vis,df;
void dfs(int x){
    dep[x] = dep[fa[x]] + 1;
    df[x] = true;
    for(node i:edge[x]){
        int y = i.to,id = i.id;
        if(df[y]) continue;
        e_tof[y] = id;//记录向父亲的边
        vis[id] = true,fa[y] = x;//记录树边和父亲
        dfs(y);
    }
}
inline void assign(int x,int y){
    vector<int> ans1,ans2,ans3;
    vector<int> pd;
    bool flag = false;
    int s,t;
    while(y != x){
        have[e_tof[y]].eb(tim);
        ring[tim].eb(y);
        if(!flag && have[e_tof[y]].size() >= 2) pd = have[e_tof[y]],flag = true,s = y;//找到了一端
        y = fa[y];
    }
    ring[tim].eb(x);
    if(!flag) return;//没有，跳过
    int id1,id2;
    y = fa[s],t = y;
    while(y != fa[x]){
        if(count(All(have[e_tof[y]]),pd[0])&&count(All(have[e_tof[y]]),pd[1])) t = fa[y];//找另一端
        else break;
        y = fa[y];
    }
    cout<<"YES\n";
    y = s;
    while(y != fa[t]) ans1.eb(y),y = fa[y];//答案一，全走树边
    int len;
 
    //答案二，走环1
    len = ring[pd[0]].size()-1;
    rep(i,0,len,1){if(ring[pd[0]][i] == s) {id1 = i;break;}}
    rep(i,0,len,1){if(ring[pd[0]][i] == t) {id2 = i;break;}}
    drep(i,id1,0,1) ans2.eb(ring[pd[0]][i]);
    drep(i,len,id2,1) ans2.eb(ring[pd[0]][i]);
 
    //答案二，走环2
    len = ring[pd[1]].size()-1;
    rep(i,0,len,1){if(ring[pd[1]][i] == s) {id1 = i;break;}}
    rep(i,0,len,1){if(ring[pd[1]][i] == t) {id2 = i;break;}}
    drep(i,id1,0,1) ans3.eb(ring[pd[1]][i]);
    drep(i,len,id2,1) ans3.eb(ring[pd[1]][i]);
    cout<<ans1.size()<<' ';for(int i:ans1) cout<<i<<' ';cout<<'\n';
    cout<<ans2.size()<<' ';for(int i:ans2) cout<<i<<' ';cout<<'\n';
    cout<<ans3.size()<<' ';for(int i:ans3) cout<<i<<' ';cout<<'\n';
    exit(0);
}
inline void get(int x,int y){
    if(dep[x] > dep[y]) swap(x,y);
    assign(x,y);
}
inline void solve(){
    cin>>n>>m;
    rep(i,1,m,1){
        cin>>u[i]>>v[i];
        add(u[i],v[i],i);
        add(v[i],u[i],i);
    }
    rep(i,1,n,1) if(!df[i]) dfs(i);
    rep(i,1,m,1){
        if(vis[i]) continue;
        tim++;
        get(u[i],v[i]);
    }
    cout<<"NO\n";
}
signed main(){
    cin.tie(nullptr)->sync_with_stdio(false);
    cout.tie(nullptr)->sync_with_stdio(false);
    solve();
}