Tarjan
强连通分量
前置知识
- 强连通 ：一张有向图的节点两两互相可达。
- 连通分量 ： 若\(H\)是\(G\)的一个连通子图，且不存在\(F\)使得\(H\subsetneq F\subseteq G\)，则\(H\)为\(G\)的一个连通分量（也叫连通块）
Tarjan求强连通分量
DFS生成树
（用的OI-wiki的图）
- 树边 ： 图中的黑边，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
- 返祖边/回边 ： 图中的红色边，指向父亲节点。
- 横叉边 ： 图中的蓝边，搜索时访问到一个已经访问过的节点，但这个节点不是当前节点的祖先。
- 前向边 ： 图中的绿边，搜索时访问到子树的节点
那么这个有什么用呢?
如果结点\(u\)是某个强连通分量在搜索树中遇到的第一个结点，那么这个强连通分量的其余结点肯定是在搜索树中以\(u\)为根的子树中。结点\(u\)被称为这个强连通分量的根。
证明
假如有一个节点\(v\)在该强连通分量中但是不在\(u\)的子树中，那么\(v\)肯定尚未访问，那么\(u\rightarrow v\)的路径中一定有一条边离开了\(u\)的子树，这样的边只能是返祖边或横叉边，然而这两条边都指向了访问过的节点，矛盾。
考虑用这个结论，得出Tarjan求强连通分量的算法
Tarjan求强连通分量
基于对图进行深度优先搜索。
先定义两个数组，对于每个节点\(u\)，有
- \(dfn_u\) （时间戳）： dfs时节点\(u\)被遍历的次序
- \(low_u\) （追溯值）： 记以\(u\)为根的子树为\(Subtree_u\)，\(low_u\)定义为\(Subtree_u\)中的节点经过一条非树边可以达到的节点的\(dfn\)的最小值。
有两个非常显然的结论，一个节点子树内的\(dfn\)都大于该点的\(dfn\)，从根开始的一条路径上，\(dfn\)单调递增，\(low\)不严格递减。提一嘴，万一以后有用呢？虽然到现在为止没用过
算法流程 ：
深度优先搜索，维护每个节点的\(dfn\)和\(low\)，将搜索到的节点入栈。假设当前搜索到的节点为\(u\)，与\(u\)连边的一个节点为\(v\)（\(v\)不是\(u\)的父亲），此时有三种情况
- \(v\)未被访问过，那么继续搜索，用\(low_v\)更新\(low_u\)
- \(v\)被访问过且已经在栈中，那么用\(dfn_v\)更新\(low_u\)
- \(v\)被访问过且不在栈中，那么表示\(v\)已经解决掉了，不需要再对其进行操作。
根据强连通分量的根为强连通分量中第一个被搜索到的节点，所以其\(dfn\)和\(low\)最小。容易得出当且仅当强连通分量的根，其\(dfn=low\)，并且强连通分量中的节点就是栈中\(u\)上方的节点。
时间复杂度\(O(n+m)\)
点此查看代码
#include<bits/stdc++.h>
#include<bits/extc++.h>
// using namespace __gnu_pbds;
// using namespace __gnu_cxx;
using namespace std;
#define infile(x) freopen(x,"r",stdin)
#define outfile(x) freopen(x,"w",stdout)
#define errfile(x) freopen(x,"w",stderr)
#define rep(i,s,t,p) for(int i = s;i <= t; i += p)
#define drep(i,s,t,p) for(int i = s;i >= t; i -= p)
#ifdef LOCAL
FILE *InFile = infile("in.in"),*OutFile = outfile("out.out");
// FILE *ErrFile=errfile("err.err");
#else
FILE *Infile = stdin,*OutFile = stdout;
//FILE *ErrFile = stderr;
#endif
using ll=long long;using ull=unsigned long long;
using db = double;using ldb = long double;
const int N = 1e4 + 10;
vector<int> edge[N];
#define eb emplace_back
inline void add(int u,int v){edge[u].eb(v);}
int n,m,dfn[N],low[N],sta[N],top,tot,num,bel[N];
bitset<N> insta,out;
vector<int> scc[N];
void Tarjan(int x){
dfn[x] = low[x] = ++tot;
sta[++top] = x;insta[x] = true;
for(int y:edge[x]){
if(!dfn[y]){
Tarjan(y);
low[x] = min(low[x],low[y]);
}
else if(insta[y]) low[x] = min(low[x],dfn[y]);
}
if(dfn[x] == low[x]){
num++;int y;
do{
y = sta[top--];
bel[y] = num;
scc[num].eb(y),insta[y] = false;
}while(y != x);
}
}
inline void solve(){
cin>>n>>m;
rep(i,1,m,1){
int u,v;cin>>u>>v;
add(u,v);
}
rep(i,1,n,1) if(!dfn[i]) Tarjan(i);
rep(i,1,num,1) sort(scc[i].begin(),scc[i].end());
cout<<num<<'\n';
rep(i,1,n,1){
if(out[bel[i]]) continue;
for(int j:scc[bel[i]]) cout<<j<<' ';
cout<<'\n';
out[bel[i]] = true;
}
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cout.tie(nullptr)->sync_with_stdio(false);
solve();
}
例题 ：
就是求强连通分量，然后看每个强连通分量的出度，如果出度为0的强连通分量有一个以上，那么无解，反之答案就是出度为0的那个强连通分量的大小
点此查看代码
#include<bits/stdc++.h>
#include<bits/extc++.h>
// using namespace __gnu_pbds;
// using namespace __gnu_cxx;
using namespace std;
#define infile(x) freopen(x,"r",stdin)
#define outfile(x) freopen(x,"w",stdout)
#define errfile(x) freopen(x,"w",stderr)
#define rep(i,s,t,p) for(int i = s;i <= t; i += p)
#define drep(i,s,t,p) for(int i = s;i >= t; i -= p)
#ifdef LOCAL
FILE *InFile = infile("in.in"),*OutFile = outfile("out.out");
// FILE *ErrFile=errfile("err.err");
#else
FILE *Infile = stdin,*OutFile = stdout;
//FILE *ErrFile = stderr;
#endif
using ll=long long;using ull=unsigned long long;
using db = double;using ldb = long double;
const int N = 1e4 + 10;
vector<int> edge[N];
#define eb emplace_back
inline void add(int u,int v){edge[u].eb(v);}
int n,m,dfn[N],low[N],sta[N],top,tot,num,bel[N],out[N],len[N];
bitset<N> insta;
void Tarjan(int x){
dfn[x] = low[x] = ++tot;
sta[++top] = x;insta[x] = true;
for(int y:edge[x]){
if(!dfn[y]){
Tarjan(y);
low[x] = min(low[x],low[y]);
}
else if(insta[y]) low[x] = min(low[x],dfn[y]);
}
if(dfn[x] == low[x]){
num++;int y;
do{
y = sta[top--];
bel[y] = num;
insta[y] = false;
len[num]++;
}while(y != x);
}
}
inline void solve(){
cin>>n>>m;
rep(i,1,m,1){
int u,v;cin>>u>>v;
add(u,v);
}
rep(i,1,n,1) if(!dfn[i]) Tarjan(i);
int ans = 0,ok = 0;
rep(x,1,n,1) for(int y:edge[x]) if(bel[x] != bel[y]) out[bel[x]]++;
rep(i,1,num,1) if(!out[i])ans = len[i],ok++;
if(ok > 1) cout<<0;
else cout<<ans;
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cout.tie(nullptr)->sync_with_stdio(false);
solve();
}
先缩点，第一问的答案就是缩完点后入度为0的点的个数，第二问的答案就是缩完点后\(\max(入度为0的点的个数，出度为0的点的个数)\)。特判只有一个强连通分量时，第一问为1，第二问为0。
点此查看代码
#include<bits/stdc++.h>
#include<bits/extc++.h>
// using namespace __gnu_pbds;
// using namespace __gnu_cxx;
using namespace std;
#define infile(x) freopen(x,"r",stdin)
#define outfile(x) freopen(x,"w",stdout)
#define errfile(x) freopen(x,"w",stderr)
#define rep(i,s,t,p) for(int i = s;i <= t; i += p)
#define drep(i,s,t,p) for(int i = s;i >= t; i -= p)
#ifdef LOCAL
FILE *InFile = infile("in.in"),*OutFile = outfile("out.out");
// FILE *ErrFile=errfile("err.err");
#else
FILE *Infile = stdin,*OutFile = stdout;
//FILE *ErrFile = stderr;
#endif
using ll=long long;using ull=unsigned long long;
using db = double;using ldb = long double;
const int N = 1e4 + 10;
#define eb emplace_back
vector<int> edge[N];
inline void add(int u,int v){edge[u].eb(v);}
int n,dfn[N],low[N],tim,tot,sta[N],top,bel[N],in[N],out[N];
bitset<N> insta;
void Tarjan(int x){
dfn[x] = low[x] = ++tim;
sta[++top] = x;insta[x] = true;
for(int y:edge[x]){
if(!dfn[y]){
Tarjan(y);
low[x] = min(low[x],low[y]);
}
else if(insta[y]) low[x] = min(low[x],dfn[y]);
}
if(dfn[x] == low[x]){
tot++;int y;
do{
y = sta[top--];
bel[y] = tot;
insta[y] = false;
}while(y != x);
}
}
inline void solve(){
cin>>n;
rep(i,1,n,1){int x; while(cin>>x&&x) add(i,x);}
rep(i,1,n,1) if(!dfn[i]) Tarjan(i);
rep(x,1,n,1) for(int y:edge[x]) if(bel[x] != bel[y]) in[bel[y]]++,out[bel[x]]++;
if(tot == 1) return cout<<"1\n0",void();
int ans1 = 0,ans2 = 0;
rep(i,1,tot,1) if(!in[i]) ans1++;
rep(i,1,tot,1) if(!out[i]) ans2++;
ans2 = max(ans1,ans2);
cout<<ans1<<'\n'<<ans2<<'\n';
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cout.tie(nullptr)->sync_with_stdio(false);
solve();
}
缩完点后跑最长路就没了
点此查看代码
#include<bits/stdc++.h>
#include<bits/extc++.h>
// using namespace __gnu_pbds;
// using namespace __gnu_cxx;
using namespace std;
#define infile(x) freopen(x,"r",stdin)
#define outfile(x) freopen(x,"w",stdout)
#define errfile(x) freopen(x,"w",stderr)
#define rep(i,s,t,p) for(int i = s;i <= t; i += p)
#define drep(i,s,t,p) for(int i = s;i >= t; i -= p)
#ifdef LOCAL
FILE *InFile = infile("in.in"),*OutFile = outfile("out.out");
// FILE *ErrFile=errfile("err.err");
#else
FILE *Infile = stdin,*OutFile = stdout;
//FILE *ErrFile = stderr;
#endif
using ll=long long;using ull=unsigned long long;
using db = double;using ldb = long double;
const int N = 5e5 + 10;
struct node{int to,w;node(int To,int W):to(To),w(W){}};vector<node> e2[N];
#define eb emplace_back
vector<int> e1[N];
int n,m,s,p,ed[N],a[N],dfn[N],low[N],tim,sta[N],top,g[N],num[N],tot;
int dist[N];
bitset<N> insta,vis;
void Tarjan(int x){
dfn[x] = low[x] = ++tim;
sta[++top] = x;insta[x] = true;
for(int y:e1[x]){
if(!dfn[y]) Tarjan(y),low[x] = min(low[x],low[y]);
else if(insta[y]) low[x] = min(low[x],dfn[y]);
}
if(dfn[x] == low[x]){
tot++;int y;
do{
y = sta[top--];
insta[y] = false;
g[y] = tot;
num[tot] += a[y];
}while(y != x);
}
}
inline void spfa(int s){
queue<int> q;q.push(s);vis[s] = true;
while(q.size()){
int x = q.front();q.pop();vis[x] = false;
for(node i:e2[x]){
int y = i.to,w = i.w;
if(dist[y] < dist[x] + w){
dist[y] = dist[x] + w;
if(!vis[y]) q.push(y),vis[y] = true;
}
}
}
}
inline void solve(){
cin>>n>>m;
rep(i,1,m,1){int u,v;cin>>u>>v;e1[u].eb(v);}
rep(i,1,n,1) cin>>a[i];
rep(i,1,n,1) if(!dfn[i]) Tarjan(i);
rep(x,1,n,1) for(int y:e1[x]) if(g[x] != g[y]) e2[g[x]].eb(node(g[y],num[g[y]]));
cin>>s>>p;rep(i,1,p,1) cin>>ed[i];
spfa(g[s]);
int ans = 0;
rep(i,1,p,1) ans = max(ans,dist[g[ed[i]]]);
cout<<ans+num[g[s]]<<'\n';
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cout.tie(nullptr)->sync_with_stdio(false);
solve();
}
双连通分量
这里的连通图均指无向连通图
前置知识
割点
对于一个连通图\(G = (V,E)\)，如果\(V^\prime\subseteq V 并且 G[V\setminus V^\prime]\)不连通，则\(V^\prime\)是图\(G\)的一个点割集，当\(|点割集|=1\)时，称其为割点。
容易发现，孤立点不是割点，孤立边的两个端点也不是割点。
点双连通 : 没有割点的连通图。
点双连通分量(V-BCC) : 一张图的极大点双连通子图，简称点双。
桥
类比割点的定义即可。
对于一个连通图\(G = (V,E)\)，如果\(E^\prime\subseteq E 并且 G = (V,E\setminus E^\prime)\)不连通，则\(E^\prime\)是图\(G\)的一个边割集，当\(|边割集|=1\)时，称其为桥。
容易发现，孤立边是割边。
边双连通 : 没有桥的连通图。
边双连通分量(E-BCC) : 一张图的极大边双连通子图，简称边双。
割点和桥
既然已经知道了割点和桥是什么，那么如何求呢?
Tarjan求割点
和强连通分量一样，还是维护两个数组\(dfn,low\)，\(dfn\)的定义同上，\(low\)的定义更改为不经过其父亲能达到的最小的时间戳。
开始进行\(dfs\)，发现对于大部分时候，\(\exists y\in son_x，low_y\ge dfn_x\)时，\(x\)为割点。就是无法不通过\(x\)回到祖先。
但是这对于搜索的起点并不成立，所以特殊考虑起点。考虑在搜索树上，如果起点只有一个儿子，那么说明删去这个点并不影响其搜索树子树内的连通性，所以其不是割点。而如果有两个及以上的儿子，那么说明删去以后这个儿子便不连通，所以此时起点也是割点。
就比如这张图，容易发现2为图中唯一的一个割点。
如果以1为起点搜索，画出来的搜索树就是这样的
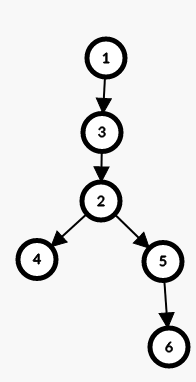
而以2为起点搜索，画出来的搜索树是这样的
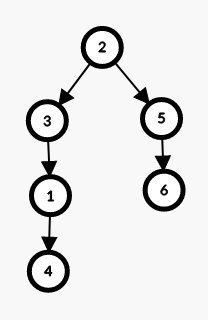
看，很符合上面说的。
点此查看代码
#include<bits/stdc++.h>
#include<bits/extc++.h>
// using namespace __gnu_pbds;
// using namespace __gnu_cxx;
using namespace std;
#define infile(x) freopen(x,"r",stdin)
#define outfile(x) freopen(x,"w",stdout)
#define errfile(x) freopen(x,"w",stderr)
#define rep(i,s,t,p) for(int i = s;i <= t; i += p)
#define drep(i,s,t,p) for(int i = s;i >= t; i -= p)
#ifdef LOCAL
FILE *InFile = infile("in.in"),*OutFile = outfile("out.out");
// FILE *ErrFile=errfile("err.err");
#else
FILE *Infile = stdin,*OutFile = stdout;
//FILE *ErrFile = stderr;
#endif
using ll=long long;using ull=unsigned long long;
using db = double;using ldb = long double;
const int N = 2e4 + 10;
int n,m,rt,dfn[N],low[N],tim;
vector<int> edge[N];
bitset<N> vis,cut;
#define eb emplace_back
void Tarjan(int x,int f){
dfn[x] = low[x] = ++tim;
vis[x] = true;
int son = 0;
for(int y:edge[x]){
if(y == f) continue;
if(!vis[y]){
Tarjan(y,x);son++;
low[x] = min(low[x],low[y]);
if(x == rt && son > 1) cut[x] = true;
if(low[y] >= dfn[x] && x != rt) cut[x] = true;
}
else low[x] = min(low[x],dfn[y]);
}
}
inline void solve(){
cin>>n>>m;
rep(i,1,m,1){int u,v;cin>>u>>v;edge[u].eb(v);edge[v].eb(u);}
rep(i,1,n,1) if(!dfn[i]) rt = i,Tarjan(i,0);
cout<<cut.count()<<'\n';
rep(i,1,n,1) if(cut[i]) cout<<i<<' ';
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cout.tie(nullptr)->sync_with_stdio(false);
solve();
}
Tarjan求割边
和求割点差不多的，就是将\(low_y\ge dfn_x\)变成\(low_y > dfn_x\)，而且不需要判断是否为根节点。
点此查看代码
#include<bits/stdc++.h>
#include<bits/extc++.h>
// using namespace __gnu_pbds;
// using namespace __gnu_cxx;
using namespace std;
#define infile(x) freopen(x,"r",stdin)
#define outfile(x) freopen(x,"w",stdout)
#define errfile(x) freopen(x,"w",stderr)
#define rep(i,s,t,p) for(int i = s;i <= t; i += p)
#define drep(i,s,t,p) for(int i = s;i >= t; i -= p)
#ifdef LOCAL
FILE *InFile = infile("in.in"),*OutFile = outfile("out.out");
// FILE *ErrFile=errfile("err.err");
#else
FILE *Infile = stdin,*OutFile = stdout;
//FILE *ErrFile = stderr;
#endif
using ll=long long;using ull=unsigned long long;
using db = double;using ldb = long double;
const int N = 1e5 + 10;
int n,m,dfn[N],low[N],tim,cnt;
vector<int> edge[N];
bitset<N> vis;
#define eb emplace_back
void Tarjan(int x,int f){
dfn[x] = low[x] = ++tim;
vis[x] = true;
int son = 0;
for(int y:edge[x]){
if(y == f) continue;
if(!vis[y]){
Tarjan(y,x);son++;
low[x] = min(low[x],low[y]);
if(low[y] > dfn[x]) cnt++;
}
else low[x] = min(low[x],dfn[y]);
}
}
inline void solve(){
cin>>n>>m;
rep(i,1,m,1){int u,v;cin>>u>>v;edge[u].eb(v);edge[v].eb(u);}
rep(i,1,n,1) if(!dfn[i]) Tarjan(i,0);
cout<<cnt;
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cout.tie(nullptr)->sync_with_stdio(false);
solve();
}
双连通分量
边双连通分量
综合了一下，还是选择了先找出桥后dfs找边双的做法，较为好理解而且不是很容易写挂。
直接写就可以了。建议还是链式前向星建图，比较好判割边。
点此查看代码
#include<bits/stdc++.h>
#include<bits/extc++.h>
// using namespace __gnu_pbds;
// using namespace __gnu_cxx;
using namespace std;
#define infile(x) freopen(x,"r",stdin)
#define outfile(x) freopen(x,"w",stdout)
#define errfile(x) freopen(x,"w",stderr)
#define rep(i,s,t,p) for(int i = s;i <= t; i += p)
#define drep(i,s,t,p) for(int i = s;i >= t; i -= p)
#ifdef LOCAL
FILE *InFile = infile("in.in"),*OutFile = outfile("out.out");
// FILE *ErrFile=errfile("err.err");
#else
FILE *Infile = stdin,*OutFile = stdout;
//FILE *ErrFile = stderr;
#endif
using ll=long long;using ull=unsigned long long;
using db = double;using ldb = long double;
const int N = 5e5 + 10,M = 4e6 + 10;
struct EDGE{int to,next;}edge[M];
int head[N],cnt = 1;
inline void add(int u,int v){edge[++cnt] = {v,head[u]};head[u] = cnt;}
vector<int> vdcc[N];int tot;
bitset<M> bri;
bitset<N> vis;
int n,m,dfn[N],low[N],tim;
void Tarjan(int x,int f){
dfn[x] = low[x] = ++tim;
vis[x] = true;
for(int i = head[x]; i;i = edge[i].next){
int y = edge[i].to;
if(y == f) continue;
if(!vis[y]){
Tarjan(y,x);
low[x] = min(low[x],low[y]);
if(low[y] > dfn[x]) bri[i] = bri[i^1] = true;
}
else low[x] = min(low[x],dfn[y]);
}
}
void dfs(int x,int f){
vis[x] = true;
vdcc[tot].emplace_back(x);
for(int i = head[x]; i;i = edge[i].next){
int y = edge[i].to;
if(bri[i] || y == f || vis[y]) continue;
dfs(y,x);
}
}
inline void solve(){
cin>>n>>m;
rep(i,1,m,1){int u,v;cin>>u>>v;add(u,v);add(v,u);}
rep(i,1,n,1) if(!dfn[i]) Tarjan(i,0);
vis.reset();
rep(i,1,n,1) if(!vis[i]) tot++,dfs(i,0);
cout<<tot<<'\n';
rep(i,1,tot,1){cout<<vdcc[i].size()<<' ';for(int j:vdcc[i]) cout<<j<<' ';cout<<'\n';}
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cout.tie(nullptr)->sync_with_stdio(false);
solve();
}
点双连通分量
对于一个点双，它在\(dfs\)搜索树中\(dfn\)值最小的点一定为割点或树根。
分类讨论：
- 这个点为割点，那么它就是点双的根
- 这个点为树根
- 有两个及以上子树，为一个割点
- 只有一个子树，它是一个点双的根
- 没有子树，视为一个点双。
点此查看代码
#include<bits/stdc++.h>
#include<bits/extc++.h>
// using namespace __gnu_pbds;
// using namespace __gnu_cxx;
using namespace std;
#define infile(x) freopen(x,"r",stdin)
#define outfile(x) freopen(x,"w",stdout)
#define errfile(x) freopen(x,"w",stderr)
#define rep(i,s,t,p) for(int i = s;i <= t; i += p)
#define drep(i,s,t,p) for(int i = s;i >= t; i -= p)
#ifdef LOCAL
FILE *InFile = infile("in.in"),*OutFile = outfile("out.out");
// FILE *ErrFile=errfile("err.err");
#else
FILE *Infile = stdin,*OutFile = stdout;
//FILE *ErrFile = stderr;
#endif
using ll=long long;using ull=unsigned long long;
using db = double;using ldb = long double;
const int N = 5e5 + 10;
vector<int> edge[N],vdcc[N];
#define eb emplace_back
int n,m,rt,dfn[N],low[N],tim,sta[N],top,tot,d[N];
bitset<N> cut;
void Tarjan(int x,int f){
dfn[x] = low[x] = ++tim;
sta[++top] = x;int son = 0;
for(int y:edge[x]){
if(!dfn[y]){
Tarjan(y,x);low[x] = min(low[x],low[y]);
if(dfn[x] <= low[y]){
son++;
if(x != rt || son > 1) cut[x] = true;
tot++;int z;
do{
z = sta[top--];
vdcc[tot].eb(z);
}while(z != y);
vdcc[tot].eb(x);
}
}
else low[x] = min(low[x],dfn[y]);
}
if(x == rt && !son) return vdcc[++tot].eb(x),void();
}
inline void solve(){
cin>>n>>m;
rep(i,1,m,1){int u,v;cin>>u>>v;edge[u].eb(v);edge[v].eb(u);}
rep(i,1,n,1) if(!dfn[i]) rt = i,Tarjan(i,0);
cout<<tot<<'\n';
rep(i,1,tot,1){
cout<<vdcc[i].size()<<' ';
for(int j:vdcc[i]) cout<<j<<' ';
cout<<'\n';
}
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cout.tie(nullptr)->sync_with_stdio(false);
solve();
}
2-SAT
定义
就是给出\(n\)个集合，每个集合有两个元素\(\{a,b\}\)，表示\(a,b\)矛盾，然后从每个集合中选择一个元素，问是否可以选出\(n\)个两两互不矛盾的元素。
解决方法
如果\(a,b\)矛盾，那么\(\neg a,b\)不矛盾，\(\neg b,a\)不矛盾，将这两对连边。
然后跑一边缩点，判断是否有\(a,b\)或者\(\neg a,\neg b\)在同一SCC中
输出方案时可以通过变量在图中的拓扑序确定该变量的取值。如果变量 \(x\) 的拓扑序在 \(\neg x\) 之后，那么取 \(x\) 值为真。应用到 Tarjan 算法的缩点，即 \(x\) 所在 SCC 编号在 \(\neg x\) 之前时，取 \(x\) 为真。因为 Tarjan 算法求强连通分量时使用了栈，所以 Tarjan 求得的 SCC 编号相当于反拓扑序。
分为四种情况讨论建图
- \(i\)为真\(j\)也为真 ：\(\neg a\rightarrow b,\neg b\rightarrow a\)
- \(i\)为真\(j\)为假 ： \(\neg a \rightarrow\neg b,b\rightarrow a\)
- \(i\)为假\(j\)为真 ： \(a\rightarrow b,\neg b\rightarrow\neg a\)
- \(i\)为假\(j\)也为假 ： \(a\rightarrow\neg b,b\rightarrow\neg a\)
然后对\(1\sim 2\times n\)跑Tarjan，如果\(\exists i\in [1,n],i与i+n\)在同一个强连通分量中，说明无解。
反之，输出解，当\(col_i < col_{i+n}\)时，值取true,反之，取false。
点此查看代码
#include<bits/stdc++.h>
#include<bits/extc++.h>
// using namespace __gnu_pbds;
// using namespace __gnu_cxx;
using namespace std;
#define infile(x) freopen(x,"r",stdin)
#define outfile(x) freopen(x,"w",stdout)
#define errfile(x) freopen(x,"w",stderr)
#define rep(i,s,t,p) for(int i = s;i <= t; i += p)
#define drep(i,s,t,p) for(int i = s;i >= t; i -= p)
#ifdef LOCAL
FILE *InFile = infile("in.in"),*OutFile = outfile("out.out");
// FILE *ErrFile=errfile("err.err");
#else
FILE *Infile = stdin,*OutFile = stdout;
//FILE *ErrFile = stderr;
#endif
using ll=long long;using ull=unsigned long long;
using db = double;using ldb = long double;
const int N = 2e6 + 10;
vector<int> edge[N];
#define eb emplace_back
inline void add(int u,int v){edge[u].eb(v);}
int n,m,dfn[N],low[N],tim,g[N],sta[N],top,num;
bitset<N> insta;
void Tarjan(int x){
dfn[x] = low[x] = ++tim;
sta[++top] = x;insta[x] = true;
for(int y:edge[x]){
if(!dfn[y]) {Tarjan(y);low[x] = min(low[x],low[y]);}
else if(insta[y]) low[x] = min(low[x],dfn[y]);
}
if(dfn[x] == low[x]){
num++;int y;
do{
y = sta[top--];
insta[y] = false;
g[y] = num;
}while(y != x);
}
}
inline void solve(){
cin>>n>>m;
rep(i,1,m,1){
int x,a,y,b;
cin>>x>>a>>y>>b;
if(a&&b) add(x+n,y),add(y+n,x);
if(a&&!b) add(x+n,y+n),add(y,x);
if(!a&&b) add(x,y),add(y+n,x+n);
if(!a&&!b) add(x,y+n),add(y,x+n);
}
rep(i,1,n<<1,1) if(!dfn[i]) Tarjan(i);
rep(i,1,n,1) if(g[i] == g[i+n]) cout<<"IMPOSSIBLE\n",exit(0);
cout<<"POSSIBLE\n";
rep(i,1,n,1) cout<<(bool)(g[i] < g[i+n])<<' ';
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cout.tie(nullptr)->sync_with_stdio(false);
solve();
}
练习 :
还是那么套路，直接套上就好啦。
点此查看代码
#include<bits/stdc++.h>
#include<bits/extc++.h>
// using namespace __gnu_pbds;
// using namespace __gnu_cxx;
using namespace std;
#define infile(x) freopen(x,"r",stdin)
#define outfile(x) freopen(x,"w",stdout)
#define errfile(x) freopen(x,"w",stderr)
#define rep(i,s,t,p) for(int i = s;i <= t; i += p)
#define drep(i,s,t,p) for(int i = s;i >= t; i -= p)
#ifdef LOCAL
FILE *InFile = infile("in.in"),*OutFile = outfile("out.out");
// FILE *ErrFile=errfile("err.err");
#else
FILE *Infile = stdin,*OutFile = stdout;
//FILE *ErrFile = stderr;
#endif
using ll=long long;using ull=unsigned long long;
using db = double;using ldb = long double;
const int N = 210;
vector<int> edge[N];//1~n 为满
#define eb emplace_back
int n,m,dfn[N],low[N],sta[N],top,tim,tot,g[N];
bitset<N> insta;
void Tarjan(int x){
dfn[x] = low[x] = ++tim;
sta[++top] = x;insta[x] = true;
for(int y:edge[x]){
if(!dfn[y]) Tarjan(y),low[x] = min(low[x],low[y]);
else if(insta[y]) low[x] = min(low[x],dfn[y]);
}
if(dfn[x] == low[x]){
tot++;int y;
do{
y = sta[top--];
insta[y] = false;
g[y] = tot;
}while(y != x);
}
}
inline void solve(){
cin>>n>>m;
tim = top = tot = 0;
rep(i,1,n<<1,1) dfn[i] = low[i] = insta[i] = g[i] = false;
rep(i,1,n<<1,1) vector<int> ().swap(edge[i]);
rep(i,1,m,1){
char x,y;int id1,id2;
cin>>x>>id1>>y>>id2;
if(x == 'm'){
if(y == 'm') edge[id1+n].eb(id2),edge[id2+n].eb(id1);
else edge[id1+n].eb(id2+n),edge[id2].eb(id1);
}
else{
if(y == 'm') edge[id1].eb(id2),edge[id2+n].eb(id1+n);
else edge[id1].eb(id2+n),edge[id2].eb(id1+n);
}
}
rep(i,1,n<<1,1) if(!dfn[i]) Tarjan(i);
bool flag = false;
rep(i,1,n,1) if(g[i] == g[i+n]){flag = true;break;}
cout<<(flag?"BAD\n":"GOOD\n");
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cout.tie(nullptr)->sync_with_stdio(false);
int T;cin>>T;while(T--)solve();
}
还是建反边跑Tarjan
点此查看代码
#include<bits/stdc++.h>
#include<bits/extc++.h>
// using namespace __gnu_pbds;
// using namespace __gnu_cxx;
using namespace std;
#define infile(x) freopen(x,"r",stdin)
#define outfile(x) freopen(x,"w",stdout)
#define errfile(x) freopen(x,"w",stderr)
#define rep(i,s,t,p) for(int i = s;i <= t; i += p)
#define drep(i,s,t,p) for(int i = s;i >= t; i -= p)
#ifdef LOCAL
FILE *InFile = infile("in.in"),*OutFile = outfile("out.out");
// FILE *ErrFile=errfile("err.err");
#else
FILE *Infile = stdin,*OutFile = stdout;
//FILE *ErrFile = stderr;
#endif
using ll=long long;using ull=unsigned long long;
using db = double;using ldb = long double;
const int N = 20010;
#define eb emplace_back
vector<int> edge[N];
inline void add(int u,int v){edge[u].eb(v);}
int n,m,dfn[N],low[N],tim,num,g[N],sta[N],top;
bitset<N> insta;
void Tarjan(int x){
dfn[x] = low[x] = ++tim;
sta[++top] = x;insta[x] = true;
for(int y:edge[x]){
if(!dfn[y]) Tarjan(y),low[x] = min(low[x],low[y]);
else if(insta[y]) low[x] = min(low[x],dfn[y]);
}
if(dfn[x] == low[x]){
num++;int y;
do{
y = sta[top--];
insta[y] = false;
g[y] = num;
}while(y != x);
}
}
inline void solve(){
cin>>n>>m;
auto opp = [](int x){return (x&1)?x+1:x-1;};
rep(i,1,m,1){
int a,b;cin>>a>>b;
add(a,opp(b));add(b,opp(a));
}
rep(i,1,n<<1,1) if(!dfn[i]) Tarjan(i);
rep(i,1,n<<1,2) if(g[i] == g[i+1]) cout<<"NIE\n",exit(0);
rep(i,1,n<<1,2) cout<<(g[i]<g[i+1]?i:i+1)<<'\n';
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cout.tie(nullptr)->sync_with_stdio(false);
solve();
}
好题。
考虑到选了第\(i\)个人就不能选择第\(i\)个人所认识的猫，所以将第\(i\)个人与其所认识的猫的主人连边，求强连通分量。
考虑到选人最好的方法就是选择一个没有出度的强连通分量，这样就可以保证直接选人即可，不用再考虑其它的限制。
深入理解一下Tarjan算法，发现找到的第一个强连通分量便没有出度。因为如果有出度的话，那么Tarjan算法就会递归进入到下一个强连通分量中，直到一个没有出度的强连通分量为止。
选的人的个数就是第一个强连通分量的个数，人就是强连通分量中的人，剩下的猫都是选手。
特判只有一个强连通分量时，无解。
点此查看代码
#include<bits/stdc++.h>
#include<bits/extc++.h>
// using namespace __gnu_pbds;
// using namespace __gnu_cxx;
using namespace std;
#define infile(x) freopen(x,"r",stdin)
#define outfile(x) freopen(x,"w",stdout)
#define errfile(x) freopen(x,"w",stderr)
#define rep(i,s,t,p) for(int i = s;i <= t; i += p)
#define drep(i,s,t,p) for(int i = s;i >= t; i -= p)
#ifdef LOCAL
FILE *InFile = infile("in.in"),*OutFile = outfile("out.out");
// FILE *ErrFile=errfile("err.err");
#else
FILE *Infile = stdin,*OutFile = stdout;
//FILE *ErrFile = stderr;
#endif
using ll=long long;using ull=unsigned long long;
using db = double;using ldb = long double;
const int N = 1e6 + 10;
#define eb emplace_back
#define All(x) x.begin(),x.end()
vector<int> edge[N];
inline void add(int u,int v){edge[u].eb(v);}
int n,m,dfn[N],low[N],tim,num,g[N],sta[N],top,len[N];
bitset<N> insta;
void Tarjan(int x){
dfn[x] = low[x] = ++tim;
sta[++top] = x;insta[x] = true;
for(int y:edge[x]){
if(!dfn[y]) Tarjan(y),low[x] = min(low[x],low[y]);
else if(insta[y]) low[x] = min(low[x],dfn[y]);
}
if(dfn[x] == low[x]){
num++;int y;
do{
y = sta[top--];
insta[y] = false;
g[y] = num;len[num]++;
}while(y != x);
}
}
inline void solve(){
cin>>n>>m;
rep(i,1,num,1) len[i] = 0;
tim = top = num = 0;
rep(i,1,n,1) vector<int>().swap(edge[i]),dfn[i] = low[i] = g[i] = insta[i] = false;
rep(i,1,m,1){
int a,b;cin>>a>>b;
if(a == b) continue;
add(a,b);
}
rep(i,1,n,1) if(!dfn[i]) Tarjan(i);
if(num == 1) return cout<<"No\n",void();
cout<<"Yes\n"<<len[1]<<' '<<n-len[1]<<'\n';
rep(i,1,n,1) if(g[i] == 1) cout<<i<<' ';
cout<<'\n';
rep(i,1,n,1) if(g[i] != 1) cout<<i<<' ';
cout<<'\n';
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cout.tie(nullptr)->sync_with_stdio(false);
int T;cin>>T;while(T--) solve();
}
好像还有一个圆方树完了，到时候再开一个写
__________________________________________________________________________________________
本文来自博客园，作者：CuFeO4，转载请注明原文链接：https://www.cnblogs.com/hzoi-Cu/p/18455109
