斜率优化dp
斜率优化
老早之前就学了,但一知半解地过了几道题就忘了
-
用途:用于解决\(f_i = min/max_{L(i)\le j\le R(i)}\{f_j+val(i,j)\}\)此类dp问题,其中当\(val\)中的每一项只与\(i\)或只与\(j\)有关时,可以考虑用单调队列优化,而当\(val\)包含\(i\)与\(j\)的乘积时,可以考虑斜率优化。
-
引入例题说明
-
先考虑暴力dp
设\(f_i\)表示已经处理好\(i\)个玩具后的最小费用,
则有\[f_i = \min{f_j+((i-j-1+\sum_{k = j+1}^iC_i)-L)^2} \]暴力dp,时间复杂度\(O(n^3)\),
利用前缀和优化,时间复杂度\(O(n^2)\)于是我们就喜提70pts
那么怎么AC此题呢
-
考虑优化暴力dp
设\(S_n\)表示\(\sum_{i=1}^n(C_i+1)\),
则式子为\(f_i = \min f_j+(S_i-S_j-L-1)^2\)
将L提前加1,得到\(f_i = \min f_j+(S_i-S_j-L)^2\)
拆开二次项,为方便去掉\(min\),化简得到
\[f_i =f_j + S_i^2-2LS_i+(L+S_j)^2-2S_iS_j \]接下来有两种理解方式
-
代数法
-
将相同的项放在一起
共有4种可能:
- 未知数只包含i的项,这类项在本次选择中的结果是不变的,在本式子中为\(S_i^2-2LS_i\)
- 未知数只包含j的项,这类项只会根据决策点不断变化,在本式子中为\(f_j+(L+S_j)^2\)(本题中表现为严格单调递增)
- 未知数既包含i又包含j的项,本式子中为\(-2S_iS_j\)
- 常数项,无论何时都不变,本式子将常数项与其它项合并
则最后的式子为
\[f_i = (S_i^2-2LS_i)+(f_j+(L+S_j)^2)-2S_iS_j \]-
维护凸包
假设有两个决策点\(j,k(0\le k<j<i)\),且决策点\(j\)优于决策点\(k\),则有
\[(S_i^2-2LS_i)+(f_j+(L+S_j)^2)-2S_iS_j\le (S_i^2-2LS_i)+(f_k+(L+S_k)^2)-2S_iS_k \]对其进行移项,用未知数只含有两个决策点\(j,k\)的式子表示未知数只含有\(i\)的式子,
\[\because j>k,C_i\ge 1 \therefore S_j-S_k>0 \]\[\begin{array}{rcl} (f_j+(L+S_j)^2)-2S_iS_j &\le & (f_k+(L+S_k)^2)-2S_iS_k\\ 2S_i(S_k-S_j) &\le & (f_k+(L+S_k)^2)-(f_j+(L+S_j)^2)\\ 2S_i &\ge & \frac{(f_k+(L+S_k)^2)-(f_j+(L+S_j)^2)}{S_k-S_j} \end{array}\]设\(Y(i) = f_i+(L+S_i)\quad X(i)=S_i\)
则有\(2S_i\ge\frac{Y(k)-Y(j)}{X(k)-X(j)}\)
也可以记作\(2S_i\ge\frac{Y(j)-Y(k)}{X(j)-X(k)}\)
等式右侧是一个关于\(P(X(k),Y(k)),P(X(j),Y(j))\)斜率式
也就是,如果存在两个决策点\(j,k(0\le k<j<i)\),满足\(2S_i\ge\frac{Y(j)-Y(k)}{X(j)-X(k)}\),则决策点\(j\)优于决策点\(k\)。
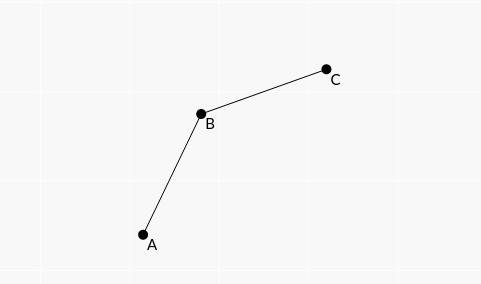
考虑如图的三个点,设\(AB\)的斜率为\(k1\),\(BC\)斜率为\(k2\)
显然的,有\(k2<k1\),设\(k=2S_i\)
根据上述结论,有
- 若\(k1\le k\),则B优于A,反之,若\(k<k1\),A优于B
- 若\(k2\le k\),则C优于B,反之,若\(k<k2\),B优于C
对\(k\)进行分类讨论有
3. 若\(k<k2<k1\),则A优于B优于C
4. 若\(k2\le k<k1\),则A,C都优于B
5. 若\(k2<k1\le k\),则C优于B优于A综上,无论如何,B永远不可能是最优决策点,将B踢出去,便只有AC
像这样维护,最终维护出了一个这样的图形
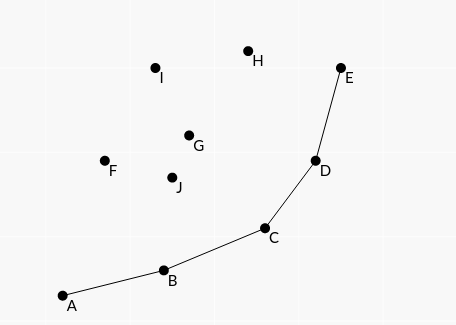
维护出了一个下凸包
同理,若将\(\frac{Y(j)-Y(k)}{X(j)-X(k)}\le k\)改为\(\frac{Y(j)-Y(k)}{X(j)-X(k)}\ge k\)(即求max),维护出的就是上凸包。
-
寻找最优决策点
由于此处斜率具有单调性,故可以用二分法找到第一个斜率大于k的线段。
-
-
线性规划
什么是线性规划
线性规划(Linear programming,简称LP),是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支,是辅助人们进行科学管理的一种数学方法,是研究线性约束条件下线性目标函数的极值问题的数学理论和方法。(节选自百度百科)dp方程:\(f_i =f_j + S_i^2-2LS_i+(L+S_j)^2-2S_iS_j\)
考虑移项,将其化成\(y=kx+b\)的形式,并使其遵循同时含有\(i,j\)的表达式为\(kx\),含有\(f_i\)的表达式位于\(b\)的位置,未知项只含有\(j\)的在\(y\)的位置,如果未知数x的表达式单调递减,最好让等式两边同乘个−1,使其变为单调递增。
该式可以化为
\[f_j+(L+S_j)^2=2S_iS_j+f_i+2LS_i-S_i^2 \]其中
\[\begin{array}{rcl} x&=&S_j\\ k&=&2S_i\\ b&=&f_i+2LS_i-S_i^2\\ y&=&f_j+(L+S_j)^2 \end{array}\]为了使\(f_i\)最小,即使\(f_i+2LS_i-S_i^2\)最小,就是使\(b\)最小,就是将\(y=kx+b\)向上平移,知道它与凸包上一点相交,则交点即最优决策点。
此时已经可以做到用二分法在\(O(n\log n)\)的复杂度中解决该问题
-
-
再优化(利用决策单调性)
-
证明决策单调性
利用四边形不等式证明决策单调性
在本题中\(w(i,j)=(S_i-S_j-L)^2\),即证明\(w(i,j+1)+w(i+1,j)\ge w(i,j)+w(i+1,j+1)\)成立
原式可以表示为
\[(S_i-S_{j+1}-L)^2+(S_{i+1}-S_j-L)^2\ge (S_i-S_j-L)^2+(S_{i+1}-S_{j+1}-L)^2 \]经历一番神奇
暴力的推导后,我们成功得到了\[w(i,j)+w(i+1,j+1)-w(i+1,j)-w(i,j+1)=-2(C_{i+1}+1)(C_{j+1}+1) \]\[\because C_i,C_j\ge 1 \]\[\therefore 2(C_{i+1}+1)(C_{j+1}+1)\le -8 \]\[\therefore w(i,j)+w(i+1,j+1)\le w(i+1,j)+w(i,j+1) \]所以具有决策单调性,用单调队列维护。
-
-
一些注意事项
- 比较斜率时尽量写上等于
- 尽量让斜率为一个整数
- 出入队列时,队列中应该至少有两个元素
- 如果斜率不得不为浮点数时,使用long double
- 大部分题都要事先在队列中加入一个0,代表决策点0
\(code:\)
点此查看代码
#include<bits/stdc++.h>
#include<bits/extc++.h>
// using namespace __gnu_pbds;
// using namespace __gnu_cxx;
using namespace std;
#define infile(x) freopen(x,"r",stdin)
#define outfile(x) freopen(x,"w",stdout)
#define errfile(x) freopen(x,"w",stderr)
using ll=long long;using ull=unsigned long long;
const int N = 5e4 + 10;
inline ll pw(ll x){return x*x;}
int n,c[N],L;
ll f[N],sum[N];
inline ll Y(int k){return f[k]+pw(L+sum[k]);}
inline long double slope(int j,int k){return 1.0*(Y(j)-Y(k))/(sum[j]-sum[k]);}
int q[N],l,r;
signed main(){
#ifndef ONLINE_JUDGE
infile("in.in");outfile("out.out");
#else
#endif
cin.tie(0)->sync_with_stdio(false);
cout.tie(0)->sync_with_stdio(false);
cin>>n>>L;L++;
for(int i = 1;i <= n; ++i) cin>>c[i];
for(int i = 1;i <= n; ++i) sum[i] = sum[i - 1] + c[i] + 1;
f[0] = 0;
l = r = 1;
for(int i = 1;i <= n; ++i){
while(l < r && slope(q[l],q[l+1]) <= 2.0*sum[i]) l++;
f[i] = f[q[l]] + pw(sum[i])-2*L*sum[i]+pw(L+sum[q[l]])-2*sum[i]*sum[q[l]];
while(l < r && slope(q[r-1],q[r]) >= slope(q[r],i)) r--;
q[++r] = i;
}
cout<<f[n];
}
-
对单调性的一些研究
-
当决策点\(x(j)\)不单调时
扔平衡树上或CDQ分治(
本人不会) -
当斜率\(k\)不单调时
二分(可以参考任务安排3)
-
都不单调时
同1,本人还是不会。
-
-
例题:
-
\(solition:\)
设\(f_i\)为已经分好前\(i\)个人,易得转移方程
\[f_i = \max f_j+a\times X^2 +b\times X + c,X = \sum_{k=j+1}^ix_k \]设\(S\)表示\(x\)的前缀和,则原式为
\[f_i=\max f_j+a\times(S_i-S_j)^2+b\times(S_i-S_j)+c \]走套路
-
去max,将相同的项放在一起,原式为
\[f_i=(f_j+aS_j^2-bS_j)+(aS_i^2+bS_i)-2aS_iS_j+c \] -
设\(0\le k<j<i\),决策点\(j\)比决策点\(k\)更优,则有
\[f_k+aS_k^2-bS_k-2aS_iS_k\le f_j+aS_j^2-bS_j-2aS_iS_j \] -
移项,用\(j,k\)的式子表示\(i\),设\(Y(x)=f_x-aS_x^2-bS_x\),\(X(x)=S_x\)
有\(Y(k)-2aS_iX(k)\le Y(j)-2aS_iX(j)\)
然后就可以维护了
\(code:\)
点此查看代码
#include<bits/stdc++.h> #include<bits/extc++.h> // using namespace __gnu_pbds; // using namespace __gnu_cxx; using namespace std; #define infile(x) freopen(x,"r",stdin) #define outfile(x) freopen(x,"w",stdout) #define errfile(x) freopen(x,"w",stderr) using ll=long long;using ull=unsigned long long; const int N = 1e6 + 10; int n,a,b,c,x[N],sum[N],q[N],l,r; ll f[N]; inline ll Y(int x){return f[x]+1ll*a*sum[x]*sum[x]-1ll*b*sum[x];} inline ll X(int x){return sum[x];} inline long double slope(int j,int k){return 1.0*(Y(k)-Y(j))/(X(k)-X(j));} signed main(){ #ifndef ONLINE_JUDGE infile("in.in");outfile("out.out"); #else #endif cin.tie(nullptr)->sync_with_stdio(false); cout.tie(nullptr)->sync_with_stdio(false); cin>>n>>a>>b>>c; for(int i = 1;i <= n; ++i) cin>>x[i]; for(int i = 1;i <= n; ++i) sum[i] = sum[i - 1] + x[i]; // memset(f,-0x3f,sizeof f); f[0] = 0; l = r = 1; for(int i = 1;i <= n; ++i){ while(l < r && slope(q[l+1],q[l]) >= 2.0*a*sum[i]) l++; int j = q[l]; f[i] = f[j] + 1ll*a*(sum[i]-sum[j])*(sum[i]-sum[j])+b*(sum[i]-sum[j])+c; while(l < r && slope(q[r-1],q[r]) <= slope(q[r],i)) r--; q[++r] = i; } cout<<f[n]; } -
-
\(solution:\)
\[f_i=\min_{j=1}^{i-1}\{f_j+\sum_{k=j+1}^{i-1}p_k(x_i-x_k)\}+C_i \]
\(to\,be\,continued\)
………………………………
本文来自博客园,作者:CuFeO4,转载请注明原文链接:https://www.cnblogs.com/hzoi-Cu/p/18285010

