算法分析与设计实验报告 Project2

实验报告

 

课程名称	《算法分析与设计》	实验日期	年   月   日至     年    月    日
学生姓名	毛潜飞	所在班级	计科195			学号	2019212212229
实验名称	实验二：Floyd和Dijkstra求解最短路
实验地点	勤13-208			同组人员

 

问题

给定点集S,边集<u,v,w>，u，v属于S,w为正整数。<u,v>表示u到v的一条映射关系。

W表示两点之间的边权，求点集中任意两点的最短路径长度。

解析

1. Floyd

我们利用动态规划的思想，设计f[k][i][j]表示只允许经过点1到k的i点到j点的最短路径长度。

那么显然k应当作为阶段，转移方程:

 

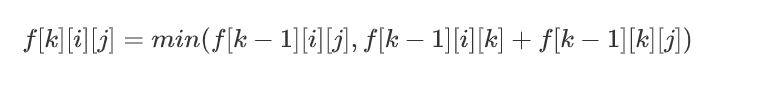
表示不经过k，或者经过k，若是后者，就需要知道i到k的最短路径和k到j的最短路径，而且我们并不关系i是怎么到k的，这就是动态规划的思想。显然我们如果把k作为阶段，这两者应该都已经被计算过了。

当然，我们的第一维可以优化掉，因为每次计算i时只利用了i-1阶段。

2.      Dijkstra

思想：将结点分为两个集合：以确定最短路的，未确定的。

一开始集合只有一个源点S，然后重复以下操作：

1. 对刚刚被加入第一个集合的结点所有出边执行松弛操作
2. 从第二个集合中，选取一个最短路最小的结点，移到第一个结点。

我们容易用贪心的思想证明其正确性。

 

设计      

FLOYD：

 

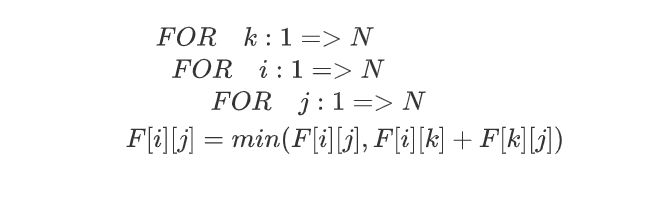
Dijkstra：

      

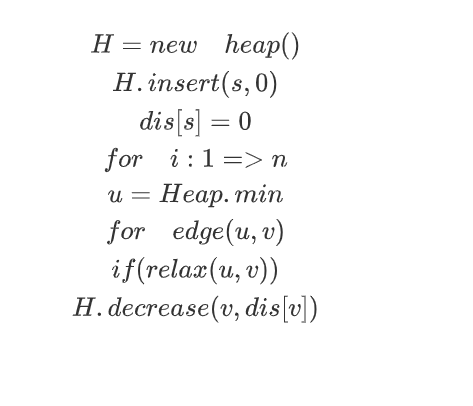
分析

       Floyd:

       代码跑了三重循环，每次循环n次，显然复杂度O(n^3)

       Dijkstra

              若我们不加任何优化，对于每个点需要拓展n个点，最多访问m条边。因此复杂度应当是O(n^2+m)

              当然，这里寻找最小我们显然可以使用堆优化，在堆中存储点。复杂度就变为了O(mlogn)

              当然，代码中为了简便使用了STL中的priority_queue，这使得堆大小最大会变成m。复杂度退化为O(mlogm)

源码

https://github.com/MQFLLY/Algorithm-Class-codes/blob/main/project2