CodeForces - 622F The Sum of the k-th Powers 拉格朗日插值模板题

定理：

{an} 是一个p阶等差数列的充要条件是数列的通项 an 为n的一个p次多项式。

题意：

求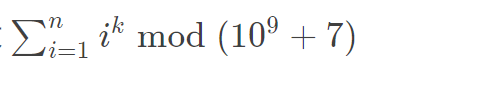

 

 这个表达式等价于一个 k + 1 次多项式。因此可以由拉格朗日插值法求得

又由于这里的x是连续的，可以预处理前缀后缀O（n）求得。

ll fac[maxn];
ll pre[maxn];
ll suf[maxn];


int main() {
    ll n = readll();
    ll k = readll();
    fac[0] = 1ll;
    pre[0] = suf[k + 3] = 1ll;
    for (int i = 1; i <= k + 2; i++)  fac[i] = fac[i - 1] * i % MOD;
    for (int i = 1; i <= k + 2; i++) pre[i] = pre[i - 1] * (n - i) % MOD;
    for (int i = k + 2; i >= 1; i--) suf[i] = suf[i + 1] * (n - i) % MOD;
    ll ans = 0;
    ll y = 0;
    for (int i = 1; i <= k + 2; i++) {
        y = (y + ksm(i, k, MOD)) % MOD;
        ll a = pre[i - 1] * suf[i + 1] % MOD;
        ll b = (fac[i - 1] *((k - i) & 1 ?  -1 : 1) * fac[k + 2 - i]) % MOD;
        b = (b + MOD) % MOD;
        ans = (ans + y * a % MOD * ksm(b, MOD - 2, MOD) % MOD + MOD) % MOD;
    }
    Put(ans);
}