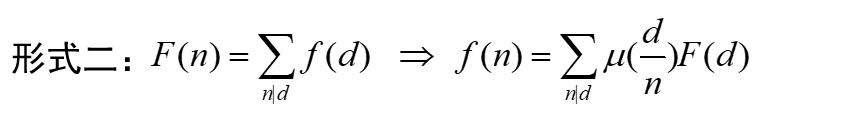51Nod 1192 Gcd表中的质数

莫比乌斯反演经典题。

借鉴大佬的推导。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

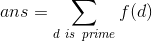
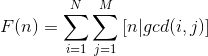
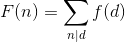
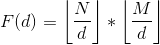
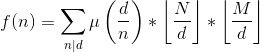
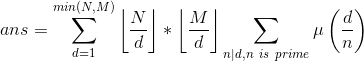
int prime[maxn], prime_tot;
int is_prime[maxn];
int mu[maxn];
ll sum[maxn];

void pre_calc(int lim) {
    mu[1] = 1;
    for (int i = 2; i <= lim; i++) {
        if (!is_prime[i]) {
            prime[++prime_tot] = i;
            mu[i] = -1;
        }
        for (int j = 1; j <= prime_tot; j++) {
            if (i * prime[j] > lim) break;
            is_prime[i * prime[j]] = 1;
            if (i % prime[j] == 0) {
                mu[i * prime[j]] = 0;
                break;
            }
            else mu[i * prime[j]] = -mu[i];
        }
    }
    for (int i = 1; i < prime_tot; i++) {
        int k = maxn / prime[i];
        for (int j = 1; j <= k; j++) sum[prime[i] * j] += mu[j];
    }
    for (int i = 0; i < maxn - 2; i++) sum[i] += sum[i - 1];
}


int main() {
    pre_calc(maxn -2);
    int T;
    int n, m;
    scanf("%d", &T);
    while (T--) {
        scanf("%d%d", &n, &m);
        if (n > m) swap(n, m);
        ll ans = 0;
        for (int l = 1, r; l <= n; l = r + 1) {
            r = min(n / (n / l), m / (m / l));
            ans += (ll)(n / l) * (m / l) * (sum[r] - sum[l - 1]);
        }
        printf("%lld\n", ans);
    }
}