Xeon第二次训练赛 by洛谷ACM训练营
A.爆炸题 图论,最短路,思维
给出一个图,从1点开始每秒为1米的速度火焰扩展,如果遇到大于一个火焰相遇就会爆炸,问最终爆炸的个数
容易得出以下规律:如果在某个点爆炸,那么这个点存在大于1的入度使得最短路相等 如果在边上爆炸,那么这条边不在最短路上

#include<iostream> #include<string> #include<cmath> #include<cstring> #include<vector> #include<map> #include<set> #include<algorithm> #include<queue> #include<stack> #include<sstream> #include<cstdio> #define INF 0x3f3f3f3f const int maxn = 300000 + 10; const double PI = acos(-1.0); typedef long long ll; using namespace std; int n, m; struct edge { int v, w; edge(int a, int b) { v = a, w = b; } };//v终点,w边权 struct node { int id, dis;//id点编号 dis暂时距离 node(int a, int b) { id = a, dis = b; } friend bool operator<(node a, node b) { return a.dis > b.dis;//每次让距离小出队 } }; vector<edge>e[maxn]; int dis[maxn];//记录最短路 bool vis[maxn];//记录是否找到最短路 int ans; void Dijkstra() { int s = 1;//s起点 根据情况改 for (int i = 0; i <= n; i++)dis[i] = INF, vis[i] = 0; dis[s] = 0; priority_queue<node>Q; Q.push(node(s, 0)); while (!Q.empty()) { node u = Q.top(); Q.pop(); if (vis[u.id])continue; vis[u.id] = 1; for (int i = 0; i < e[u.id].size(); i++) {//遍历邻居 edge y = e[u.id][i]; if (vis[y.v])continue; if (dis[y.v] > y.w + dis[u.id]) { dis[y.v] = y.w + u.dis; Q.push(node(y.v, dis[y.v]));//更新最短路 } } } } int main() { scanf("%d%d", &n, &m); int u, v, w; for (int i = 0; i < m; i++) { scanf("%d%d%d", &u, &v, &w); e[u].push_back(edge(v, w)); if (u != v) e[v].push_back(edge(u, w)); } Dijkstra(); //for (int i = 1; i <= n; i++) printf("%d ", dis[i]); for (int i = 1; i <= n; i++) { int cnt = 0; for (int j = 0; j < e[i].size(); j++) { if (dis[i] == dis[e[i][j].v] + e[i][j].w) cnt++; else if (i >= e[i][j].v && dis[i] + e[i][j].w > dis[e[i][j].v] && dis[e[i][j].v] + e[i][j].w > dis[i]) ans++; //core } if (cnt > 1) ans++; } printf("%d", ans); return 0; }
B. 模拟题/公式题
其实就是给出日期,求过n天后的日期

#include <bits/stdc++.h> using namespace std; inline void read(int &a) { int ch = getchar(); while (ch < '0') ch = getchar(); a = 0; while (ch >= '0') a = a * 10 + ch - '0', ch = getchar(); } int M[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}; void work() { int Mo, y, m, d; read(Mo); read(y); read(m); read(d); int del = 0; while (Mo < int(1e9)) { del++; Mo += del; if (++d > M[m] + (m == 2 && y % 4 == 0 && (y % 100 != 0 || y % 400 == 0))) { d = 1; if (++m == 13) y ++, m = 1; } } printf("%d %d %d\n", y, m, d); } int main() { int T; read(T); while (T--) work(); return 0; }
C.下次一定
D.给出a,b,k,gcd(a,b)=1 求满足 方程 ax+by=c, ab<0的第k小的c
数论题,不是很有想法
暂时用暴力法

#include<iostream> #include<string> #include<cmath> #include<cstring> #include<vector> #include<map> #include<set> #include<algorithm> #include<queue> #include<stack> #include<sstream> #include<cstdio> #define INF 0x3f3f3f3f const int maxn = 1e7+5; const double PI = acos(-1.0); typedef long long ll; using namespace std; int f[maxn]; int main() { int T; int a, b, c, now,i; scanf("%d", &T); while (T--) { ll k, sum=0; c = now = 0; if (a > b) swap(a, b); memset(f, 0, sizeof f); for (i = 0; sum < k; i++) { while (c < b) { f[c] = 1; c += a; now++; } c -= b; sum += b - now; } for (int j = b - 1; j; j--) { if (!f[j]) { if (sum == k) { printf("%lld", (i - 1) * b + j); break; } sum--; } } } return 0; }
E.给出一段字符串,按题给要求对字符串进行修改 题给要求是符合一定机高级语言逻辑的自然语言
解法:利用编辑器的查找替换功能

#include<bits/stdc++.h> using namespace std; typedef long long ll; int main(){ string name; cin>>name; if ( name[0] != 'g') { reverse(name.begin(),name.end());} else { name += 'h';} if ( name[name.length()-1] != 'y' && name[0] == 'w') { name += 'j';} else { name += 't';} if ( name.length() <= 42) { name += 'u';} else { ;} if ( name[name.length()-1] != 'v') { reverse(name.begin(),name.end());} else { name += 'd';} if ( name.length() <= 43) { name += 'o';} else { name += 'q';} if ( name[0] != 'm') { reverse(name.begin(),name.end());} else { reverse(name.begin(),name.end());} if ( name[name.length()-1] == 'x') { ;} else { name += 's';} if ( name.length() < 22) { name += 'n';} else { name += 't';} if ( name[0] != 'i') { ;} else { reverse(name.begin(),name.end());} if ( name[name.length()-1] == 'c') { name += 'e';} else { name += 'a';} if ( name.length() != 42 && name[name.length()-1] == 'v') { name += 'u';} else { ;} if ( name.length() >= 47) { name += 'j';} else { reverse(name.begin(),name.end());} if ( name[0] != 'v') { name += 'e';} else { name += 'd';} if ( name[name.length()-1] == 'y') { name += 'w';} else { reverse(name.begin(),name.end());} if ( name[0] == 'u') { reverse(name.begin(),name.end());} else { name += 'i';} if ( name.length() >= 32) { name += 'w';} else { ;} if ( name[name.length()-1] != 'i' && name[0] == 'd') { name += 'a';} else { reverse(name.begin(),name.end());} if ( name[name.length()-1] != 'y') { reverse(name.begin(),name.end());} else { ;} if ( name[0] == 'y') { name += 'v';} else { reverse(name.begin(),name.end());} if ( name.length() > 50) { ;} else { name += 'm';} if ( name[name.length()-1] == 't') { name += 'w';} else { name += 'q';} if ( name[0] == 't') { name += 'e';} else { ;} if ( name.length() > 48) { name += 'l';} else { reverse(name.begin(),name.end());} if ( name[name.length()-1] == 'y') { name += 'w';} else { reverse(name.begin(),name.end());} if ( name.length() >= 18 && name[0] != 'b') { reverse(name.begin(),name.end());} else { name += 'c';} if ( name.length() > 18) { name += 'y';} else { ;} if ( name[name.length()-1] != 'g') { name += 'a';} else { reverse(name.begin(),name.end());} if ( name[0] == 'q') { ;} else { name += 'i';} if ( name[name.length()-1] == 'n' && name.length() >= 38) { name += 'o';} else { name += 'v';} if ( name[0] != 'n') { ;} else { name += 'z';} if ( name.length() == 21 && name[0] != 'm') { name += 'u';} else { name += 'o';} if ( name.length() == 34) { ;} else { name += 'z';} if ( name[0] != 'r') { reverse(name.begin(),name.end());} else { reverse(name.begin(),name.end());} if ( name.length() > 25) { name += 'c';} else { reverse(name.begin(),name.end());} if ( name[0] != 'u') { name += 'k';} else { name += 'l';} if ( name.length() < 41) { reverse(name.begin(),name.end());} else { name += 'p';} if ( name[0] != 'p') { reverse(name.begin(),name.end());} else { name += 'z';} if ( name.length() < 4 && name[name.length()-1] == 'p') { reverse(name.begin(),name.end());} else { name += 'l';} if ( name.length() != 16 && name[0] == 'w') { name += 'r';} else { name += 'o';} if ( name[name.length()-1] == 'c') { name += 'p';} else { name += 'i';} if ( name.length() != 20) { name += 'p';} else { reverse(name.begin(),name.end());} if ( name[name.length()-1] != 'b') { reverse(name.begin(),name.end());} else { name += 'p';} if ( name[0] != 'c') { name += 'n';} else { name += 'l';} if ( name.length() <= 40) { name += 'd';} else { ;} if ( name[0] == 'g') { name += 'y';} else { name += 'i';} if ( name[name.length()-1] == 'k') { reverse(name.begin(),name.end());} else { name += 'v';} if ( name.length() != 20 && name[0] != 'u') { reverse(name.begin(),name.end());} else { reverse(name.begin(),name.end());} if ( name.length() <= 46) { name += 'v';} else { name += 'f';} if ( name[0] != 'i') { ;} else { name += 'z';} if ( name.length() >= 38) { reverse(name.begin(),name.end());} else { name += 'b';} cout<<name<<endl; return 0; }
F. 拉克丝放大招的同时提莫可以运动s的直线距离,求经过运动后拉克丝大到提莫的概率 ,拉克丝大招可以视为一个长度无限,宽度为w的矩形
题解:提莫最终的位置形成的集合是一个圆环,由此拉克丝的大招可以进化成一个宽度w+d的矩形,提莫退化成一个点,可以通过求导证明相切时有最大比值

#include <bits/stdc++.h> using namespace std; long double w, r, d, s; void work() { int W, R, D, S; scanf("%d%d%d%d", &W, &R, &S, &D); W += R; if (W >= 2 * S) puts("1.000000000"); else if (W == 0) puts("0.000000000"); else { w = W, d = D, s = S; long double a = s - w; long double deg = acosl(a / s); printf("%.9lf\n", double(deg / acosl(-1))); } } int main() { int T; scanf("%d", &T); while (T--) work(); }
G. 给出一个偶数,输出两个素数,两素数和是这个偶数,考虑时间复杂度够用直接枚举

#include<iostream> #include<string> #include<cmath> #include<cstring> #include<vector> #include<map> #include<set> #include<algorithm> #include<queue> #include<stack> #include<sstream> #include<cstdio> #define INF 0x3f3f3f3f //const int maxn = 1e9 + 5; const double PI = acos(-1.0); typedef long long ll; using namespace std; bool check(int x) { for (int i = 2; i <=sqrt(x); i++) { if (x % i == 0) return false; } return true; } int main() { int n; scanf("%d", &n); int mid = n >> 1; int l, r; if(mid&1) { l = r = mid; while (l > 1) { if (check(l) && check(r)) { printf("%d %d", l, r); break; } l -= 2, r += 2; } } else { l = mid - 1; r = mid + 1; while (l > 1) { if (check(l) && check(r)) { printf("%d %d", l, r); break; } l -= 2, r += 2; } } return 0; }
H.给出一颗树,每个结点都有颜色,求每个结点的分数,分数计算方式为以这个结点为根构成的树中所有颜色相同子节点的最短距离的和。如图示
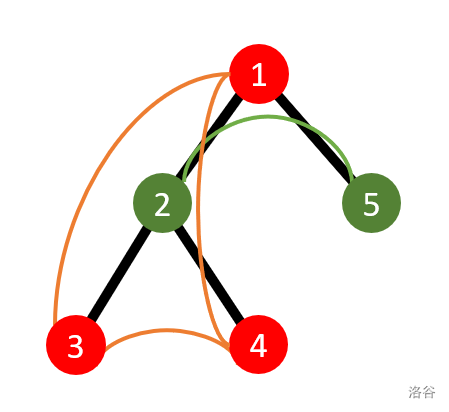
上图输出应该为 8 2 0 0 0
策略是通过合并结点来枚举每个结点的分数 可以用线段树也可以用红黑树(map)合并,map的小标表示颜色信息,遍历map来计算距离
这里给出fyh的图解来帮助理解
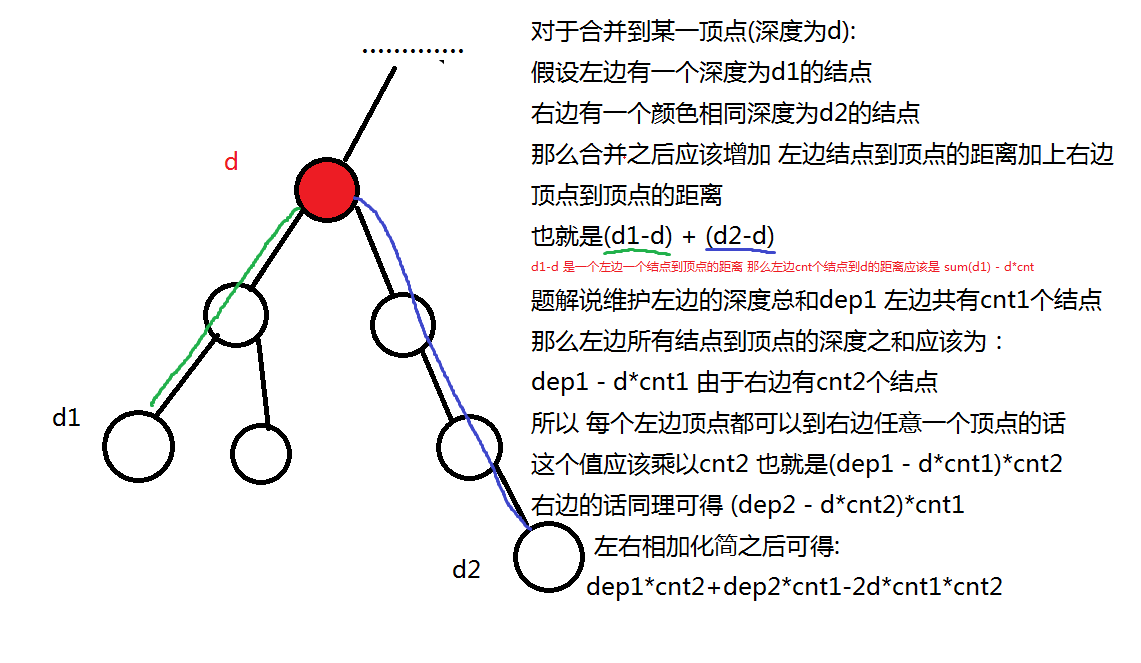
参考代码 可以学习的点 auto&v :b 来代替迭代器的for循环

#include <bits/stdc++.h> using namespace std; typedef long long LL; typedef pair<int, int> pii; #define N 101111 int n; int a[N], dep[N]; typedef map <int, pair<long long, int>> Map; Map rt[N]; vector <int> E[N]; LL sc[N], delta; int curdep; void Merge(Map &a, Map &b) { if (a.size() < b.size()) swap(a, b); for (auto& v : b) { int col = v.first; auto it = a.find(col); if (it != a.end()) { LL d1 = it->second.first, c1 = it->second.second; LL d2 = v.second.first, c2 = v.second.second; delta += d1 * c2 + d2 * c1 - 2ll * curdep * c1 * c2; it->second.first += d2; it->second.second += int(c2); } else { a.insert(v); } } } void init(Map& r, int p) { r[p] = {curdep, 1}; } void dfs(int x, int fa) { curdep = dep[x]; init(rt[x], a[x]); for (auto v : E[x]) if (v != fa){ dep[v] = dep[x] + 1; dfs(v, x); sc[x] += sc[v]; delta = 0; curdep = dep[x]; Merge(rt[x], rt[v]); sc[x] += delta; } } int main() { scanf("%d", &n); for (int i = 1; i <= n; i++) scanf("%d", a + i); for (int i = 1; i < n; i++) { int u, v; scanf("%d%d", &u, &v); E[u].push_back(v); E[v].push_back(u); } dfs(1, -1); for (int i = 1; i <= n; i++) printf("%lld ", sc[i]); }


