HZNU-ACM寒假集训Day12小结 数论入门 题解

  算不出的等式

  BJOI2012

  

 

 

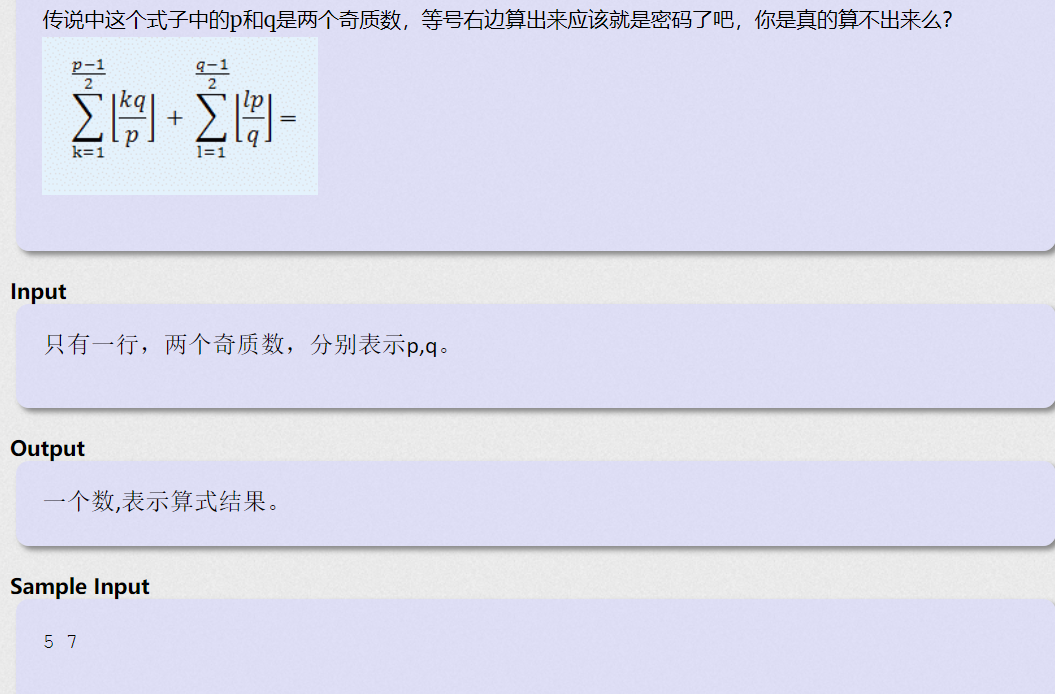
    看到这题 真没什么办法 无奈看题解

    1.注意到p/q 联想到斜率

    2.注意到 [ ] 联想到整点

    注意到k在变化，构造一次函数 f(x)=p/q*x ,g(x)=q/p*x

   

 

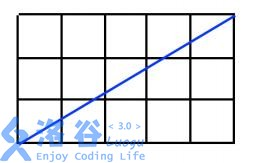
   收到【】 的影响，y值即为f(x)下取整后的值，即垂线上整点的个数

   又考虑到p==q时 需特判

   于是有

#include<iostream>
#include<cstdio>
#include<string>
#include<algorithm>
#include<queue>
#include<deque>
#include<set>
#include<map>
#include<cmath>
#include<cstring>
#include<stack>
const double PI = acos(-1.0);
#define eps 1e-6
#define INF 0x3f3f3f3f
typedef long long ll;
using namespace std;

int main() {
    ll x, y;
    scanf("%lld%lld", &x, &y);
    if (x != y) printf("%lld", (x - 1) / 2 * (y - 1) / 2);
    else printf("%lld", x * x / 4);
    return 0;
}

  HDU4475

  

 

  通过找规律易得出 递推式 aⁿ=a^n-1*2*(n-1) 

  这里可以直接预处理

  

#include<iostream>
#include<cstdio>
#include<string>
#include<algorithm>
#include<queue>
#include<deque>
#include<set>
#include<map>
#include<cmath>
#include<cstring>
#include<stack>
const double PI = acos(-1.0);
#define eps 1e-6
#define INF 0x3f3f3f3f
#define MOD 1000003
typedef long long ll;
using namespace std;

ll a[MOD+10];


void fac() {
    a[0] = 1;
    for (int i = 1; i <= MOD; i++) {
        a[i] = ((2 * a[i - 1]) * (i)) % MOD;
    }
}

int main() {
    fac();
    int T;
    ll n;
    scanf("%d", &T);
    while (T--) {
        scanf("%lld", &n);
        if (n >=MOD) {
            printf("0\n"); continue;
        }
        ll ans = a[n];
        printf("%lld\n", ans);
    }
     return 0;
}

  洛谷 P1372 又是毕业季I

   “

   此题简化后，求的是：从1~n中取k个数，使这k个数的最大公约数最大

   因为两个数成倍数关系时，它们的最大公因数是两数中的较小数，也就是相对来说最大公因数较大

   返回题目，这k个数其实就是：x*1,x*2......x*k，及x的1~k倍，但必须保证x*k小于n，在上述条件下，能知道，符合条件的最大的x就是答案，为了找出最大的x，必须使x*k尽量接近n，因为c++的整数除法有自动取整的功能，所以所有情况下，n/k都是最终答案

”   by _wc_

   

#include<iostream>
#include<cstdio>
#include<string>
#include<algorithm>
#include<queue>
#include<deque>
#include<set>
#include<map>
#include<cmath>
#include<cstring>
#include<stack>
const double PI = acos(-1.0);
#define eps 1e-6
#define INF 0x3f3f3f3f
typedef long long ll;
using namespace std;

ll n, k;

int main() {
    cin >> n >> k;
    cout << n / k;
    return 0;
}

  

  HDU 4704

 

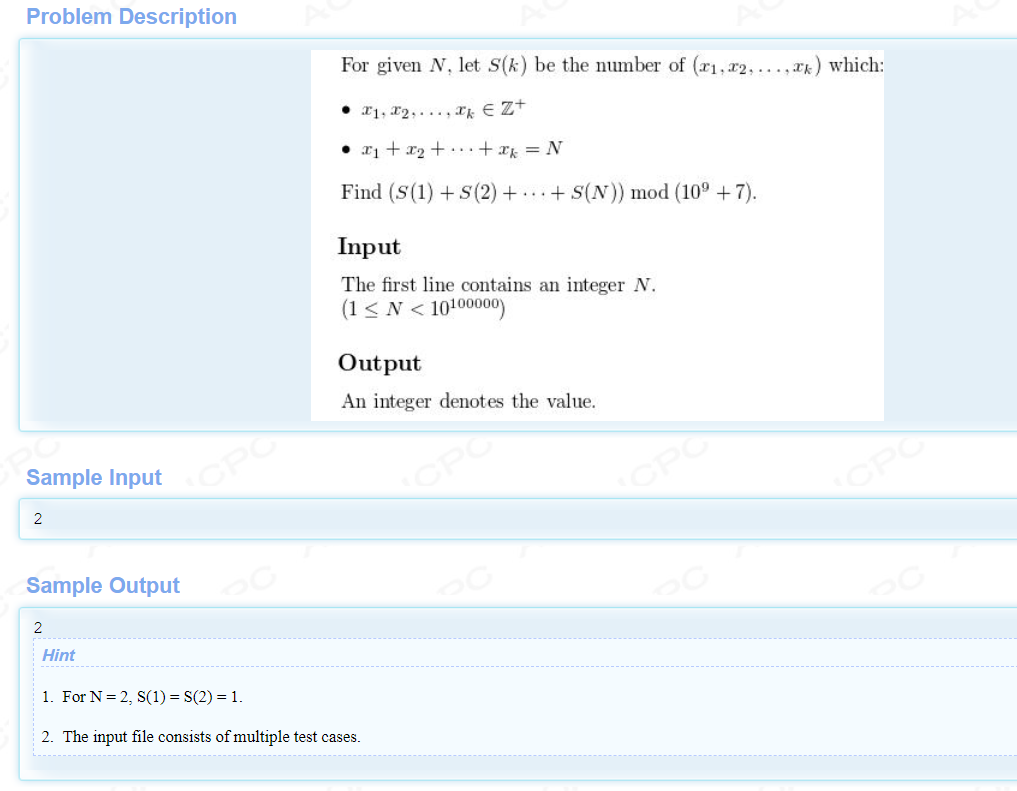
   S(k) 表示用k个x的不定方程解的个数   可以把xi看成xi个1的和，所以最后是C（n-1)（k）

  答案即为 2^n-1    

  可以用费马小定理或欧拉定理优化

  

#include<iostream>
#include<cstdio>
#include<string>
#include<algorithm>
#include<queue>
#include<deque>
#include<set>
#include<map>
#include<cmath>
#include<cstring>
#include<stack>
const double PI = acos(-1.0);
#define eps 1e-6
#define INF 0x3f3f3f3f
typedef long long ll;
using namespace std;

const int maxn = 1e5 + 5;
char a[maxn];

ll quickPower(ll a, ll b,ll m) {
    ll ans = 1;
    ll base = a;
    while (b) {
        if (b & 1) {
            ans *= base;
            ans %= m;
        }
        base *= base;
        base %= m;
        b >>= 1;
    }
    return ans;
}

int main() {
    ll MOD = 1e9 + 5;
    while (scanf("%s", a) != EOF) {
         
        int len = strlen(a);
        ll ans = 0;
        for (int i = 0; i < len; i++) {
            ans = (ans * 10 + a[i] - '0') % (MOD - 1);
        }
        ans = (ans - 1 + MOD - 1) % (MOD - 1);
        printf("%lld\n", quickPower(2, ans,MOD));
    }
    return 0;
}