AC自动机

unimportant博客背景：总结知识点的原因是，不看题解搞不出题了所以决定巩固基础图片来自

预(xia)备(che)知识

首先你要知道他不能帮你自动AC，还可能一直WA，AC自动机是在trie树上跑的KMP，所以预备知识就是KMP+trie树了，我觉得吧trie是载体，而KMP是思想，KMP和AC自动机的差别的话，前者是单模式串匹配，后者是多模式串匹配。举个栗子，给你一个短串和一个长串，让你查询短串是否在长串出现过，HASH，KMP随便选开心就好，但是如果让你模拟WPS中的查找操作呢？就是给你n个短串和一个较长的文本，查询每一个短串是否在文本中出现过以及出现次数，如果n很大的话KMP超时妥妥的，这时候AC自动机就出场了

由于本人蒟蒻，指针还没学，就学的数组的，可能会比指针慢一点，Keywords Search那道题我用数组在我们的oj上跑了129ms还凑合吧

既然AC自动机是在trie树上跑的KMP，那我们就需要先有trie树，这个就不过多赘述了，当然我在缘分的驱使下学了trie图，图和树的区别就在于图会把某一行没有的点指到它父节点的失败指针的跟他相同的儿子那里，注意是点而不是失败指针，而trie树则不管这些乱七八糟没有的点(这是我的大佬同学告诉我的，具体有关trie图的知识我觉得这篇博客还算详细，比较好懂)

对于ash shex bcd sha四个模式串构建出来的trie如图

 

trie树搞定之后就到了关键的fail指针的构建，这个和KMP的next数组有异曲同工之妙，所谓的fail指针就是找到失配位置可以匹配的另一个位置，比如在已经构建好的trie中，要找第二行的s的失败指针就指向第一行的s，失配指针存在的意义就是避免没有意义的不断回溯

全部搞好之后就像这样

 

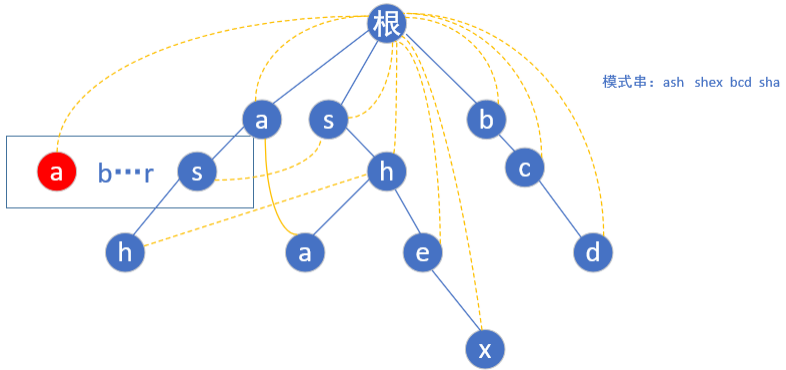
那剩下要做的就是在搞好的trie图上跑KMP匹配了，假设给定文本串ashexbcdg问在该文本串中出现了几个模式串，ash一路匹配配到h发现是一个串的末尾，ans++，接下来h后面没有字母了，就找到h的失配，第二行的h一路匹配hex又一次++，发现x失配指向了根，就从根开始bcd匹配，ans++，d指向根，找不到可匹配的g，程序结束，输出ans==3

#include<iostream>
#include<string>
#include<cstring>
#include<cstdio>
using namespace std;
const int N=500005;
int ans,tot,fail[N],trie[N][28],ed[N],que[N];
char s[N<<1];
void charu(char *s)
{
    int u=1,len=strlen(s);
    for(int i=0;i<len;++i)
    {
        int c=s[i]-'a'+1;
        if(!trie[u][c])  {trie[u][c]=++tot;  memset(trie[tot],0,sizeof(trie[tot]));}
        u=trie[u][c];
    }
    ed[u]++;
}
void FAIL()
{
    for(int i=1;i<=26;++i)  trie[0][i]=1;
    que[1]=1;  fail[1]=0;
    int le=1,ri=1;
    while(le<=ri)
    {
        int u=que[le];
        le++;
        for(int i=1;i<=26;++i)
        {
            if(!trie[u][i])  trie[u][i]=trie[fail[u]][i];
            else
            {
                que[++ri]=trie[u][i];
                int v=fail[u];
                fail[trie[u][i]]=trie[v][i];
            }
        }
    }
}
void chaxun(char *s)
{
    int u=1,len=strlen(s);
    for(int i=0;i<len;++i)
    {
        int c=s[i]-'a'+1;
        int k=trie[u][c];
        while(k>1)  {ans+=ed[k];  ed[k]=0;  k=fail[k];}
        u=trie[u][c];
    }
}
int main()
{
    int t;  scanf("%d",&t);
    while(t--)
    {
        int n;  scanf("%d",&n);
        ans=0;  tot=1;
        memset(ed,0,sizeof(ed));
        for(int i=1;i<=26;i++)  {trie[0][i]=1;  trie[1][i]=0;}
        for(int i=1;i<=n;++i)  {scanf("%s",s);  charu(s);}
        FAIL();
        scanf("%s",s);  chaxun(s);
        printf("%d\n",ans);
    }
    return 0;
}