组合数学
今天又是打不出题来的颓废的一天,排列组合一个高考不太难,搬进奥赛就啥都不会的专题
对于很多计数类问题,有很多看到取模的模数就能想象到结果有多大,显然对于这一类问题搜索是不能解决的(当然,如果你觉得自己有足够的时间,那你搜索我也没意见),组合数学便是对这些计数类问题进行优化
计数原理
1.加法原理
举个例子:从甲地到乙地有海陆空三种选择,坐船有3班,坐车有5班,坐飞机有2班,问从甲地到乙地共几种选择
解:这就是个幼儿园的题3+5+2=10
加法原理(分类计数原理):完成一件事情共有n类方法,第一类方法有$n_1$种方案,第二类有$n_2$种方案…那么完成这一件事共有$n_1+n_2+n_3+{\cdots}$种方法,注意分类需要不重不漏
2.乘法原理
依旧举个例子:从甲地到乙地需要途径A地,从甲地到A地有5种方法,从A地到乙地有3种方法,问从甲地到乙地共有几种选择
解:这个大概要小学水平了$5{\times}3=15$
乘法原理(分步计数原理):完成一件事需要分成n步进行,第一步有$n_1$种方法,第二步有$n_2$种方法…那么完成这件事共有$n_1{\times}n2{\times}{\cdots}$种方法,依旧不重不漏
排列与组合
1.排列:从n个不同的元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列,用符号$A_n^m$表示
$A_n^m=n{\times}(n-1){\times}(n-2){\times}{\cdots}{\times}{n-m+1}=\frac{n!}{(n-m)!}$
2.组合:从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号$C_n^m$表示
$C_n^m=\frac{A_n^m}{A_m^m}=\frac{n!}{m!{\times}(n-m)!}$
几种常用策略/方法
1)特殊元素和特殊位置优先策略
例:由0,1,2,3,4,5可组成多少个没有重复数字的五位奇数
解:由于末位和首位有特殊要求,应该优先安排,以免不合要求的元素占了这两个位置。
先排末位共有$C_3^1$,然后排首位共有$C_4^1$,最后排其它位置共有$A_4^3$
由分步计数原理得$ans=C_3^1{\times}C_4^1{\times}A_4^3$
2)相邻元素捆绑策略
例:7人站成一排 ,其中甲乙相邻,且丙丁相邻, 共有多少种不同的排法.
解:先将甲乙两元素捆绑成整体并看成一个复合元素,同时丙丁也看成一个复合元素,再与其它元素进行排列,同时对相邻元素内部进行自排。
由分步计数原理可得共$A_5^5{\times}A_2^2{\times}A_2^2$种不同的排法。
例:记者要为5名志愿者和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,求不同排法的数量。
解:第一步排两端,共有$C_5^1{\times}C_4^1$(或$A_5^2$)种排列方式
第二步将两个老人看作一个整体和剩余4个志愿者全排列,有$A_4^4$种排列方式
第三步两个老人内部全排列,有$A_2^2$种排列方式
所以共$A_5^2{\times}A_4^4{\times}A_2^2$种排列方式
3)不相邻问题插空策略
例:一个晚会的节目有4个舞蹈,2个相声,3个独唱,舞蹈节目不能连续出场,则节目的出场顺序有多少种?
解:第一步,排列2个相声和3个独唱,共有$A_5^5$种方案
第二步,将四种舞蹈插入第一步排好的5个元素中间包含首尾两个空位共有$A_4^6$种不同的方法,节目的不同顺序共有$A_5^5{\times}A_6^4$种。
不相邻问题通常用插空法:
把要求不相邻的元素放在一边,先排其他元素,再将不相邻的元素插在已经排好的元素之间的空位上。
4)定序问题倍缩空位插入策略
例:7人排队,其中甲乙丙3人顺序一定,共有多少不同的排法
解:共有不同排法种数是$\frac{A_7^7}{A_3^3}$
(倍缩法)对于某几个元素顺序一定的排列问题,可先把这几个元素与其他元素一起进行排列,然后用总排列数除以这几个元素之间的全排列数
5)排列问题求幂策略
例:把6名实习生分配到7个车间实习,共有多少种不同的分法
解:完成此事共分六步:把第一名实习生分配到车间有7种分法,把第二名实习生分配到车间也有7种分法
依此类推,由乘法原理共有$7^6$种不同的排法。
6)环排问题线排策略
例:8人围桌而坐,共有多少种坐法?
解:围桌而坐与坐成一排的不同点在于,坐成圆形没有首尾之分,所以固定一人,并从此位置把圆形展成直线其余7人共有(8-1)!=7!种排法
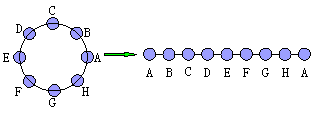
一般地,n个不同元素作圆形排列,共有(n-1)!种排法
如果从n个不同元素中取出m个元素作圆形排列,共有$\frac{A_n^m}{m}$种排法
7)多排问题直排策略
例:8人排成前后两排,每排4人,其中甲乙在前排,丙在后排,共有多少排法
解:8人排前后两排,相当于8人坐8把椅子,可以把椅子排成一排。
前排有2个特殊元素,方案数为$A_4^2$
后4个位置上有一个特殊元素丙,方案数为$A_4^1$
其余的5人在5个位置上任意排列,方案数为$A_5^5$
共有$A_4^2{\times}A_4^1{\times}A_5^5$种方案
8)排列组合混合问题先选后排策略
例:有5个不同的小球,装入4个不同的盒内,每盒至少装一个球,求共有多少不同的装法
解:第一步从5个球中选出2个组成复合元共有$C_5^2$种方法.再把4个元素(包含一个复合元素)装入4个不同的盒内有$A_4^4$种方法
根据分步计数原理装球的方法共有$C_5^2{\times}A_4^4$。
9)平均分组问题除法策略
例:6本不同的书平均分成3堆,每堆2本共有多少分法
解:分三步取书得$C_6^2{\times}C_4^2{\times}C_2^2$种方法,但这里出现重复计数的现象,每种方案计算了$A_3^3$次,故最终答案为$\frac{C_6^2{\times}C_4^2{\times}C_2^2}{A_3^3}$
10)重排列
例:由四面红旗,三面蓝旗,二面黄旗,五面绿旗排成的一排彩旗有多少种?
解:将14面彩旗排成一个排列,方案数$A_{14}^{14}$,其中红旗之间每种排列等价,方案数$A_4^4$,以此类推
共有$\frac{A_{14}^{14}}{A_4^4{\times}A_3^3{\times}A_2^2{\times}A_5^5}$种
常用结论
将一个长度为n的序列划分成m段非空子串的方案数为$C_{n-1}^{m-1}$,相当于在n-1个空位中选择m-1个插入隔板的方案数
将一个长度为n个序列划分成m段可空子串的方案数为$C_{m+n-1}^{m-1}$,相当于在m+n-1个位置中选择m-1个作为隔板的方案数
博客内容摘自PPT


