平衡树SPLAY
一个比线段树代码还要又臭又长的数据结构,各式各样的函数,咱也不知道别人怎么记住的,咱也不敢问
SPLAY的性质
1.某个节点的左子树全部小于此节点,右子树全部大于此节点
2.中序遍历splay输出的序列是按从小到大的顺序
(我当时忽略了性质2,以为大小关系只存在于单独的左右儿子和父节点,后来问了同学才知道,我没看过二叉排序树,我能怎么办)
询问左右儿子
就是查询一下x是fa的左儿子还是右儿子
int get(int x) { return a[a[x].fu].son[1]==x; }
更新数据
由于每次翻转之后左右儿子的信息都会改变,所以需要更新一下size
void gx(int x) { a[x].size=a[a[x].son[0]].size+a[a[x].son[1]].size+a[x].js; }
上旋
什么是上旋呢,简单来说就是儿子想当爹,然后他还成功了,也不知道这个爹会不会被气死,就是把自己父节点变成自己的一个儿子,但是对于一个有两个子节点的子节点,显然父节点没地方去,又因为需要保证平衡树的性质(左子树小于父节点小于右子树),所以肯定子节点的某一个叶节点要去给父节点当儿子,根据splay性质中的大小关系,如果子节点是父节点的左儿子那父节点就要去当子节点的右儿子,此时根据splay的性质直接让子节点的右儿子去当父节点的左儿子即可,这样就完成了一次翻转并且没有改变splay的性质,若子节点是父节点的右儿子,同理交换儿子,总结一下就是假设右旋x,x是fa的0儿子就让x的1儿子去当fa的0儿子,fa变成x的1儿子(0和1就是一个左一个右)
void sx(int x) { int f=a[x].fu,ff=a[f].fu; int z1=get(x),z2=get(f); a[f].son[z1]=a[x].son[z1^1]; a[a[x].son[z1^1]].fu=f; a[x].son[z1^1]=f; a[f].fu=x; a[ff].son[z2]=x; a[x].fu=ff; gx(f); gx(x); }
双旋
我觉得双旋就是上旋中的一种特殊情况,就是子节点,父节点,祖父节点在同一条线上,这时需要先上旋父节点(据说直接上旋慢,不够优秀,而且双旋好像还可以减小期望深度,我并没有模拟),同一条线的话,特判一下就可以了,记得更新根节点
void splay(int x,int mb) { while(a[x].fu!=mb) { int f=a[x].fu,ff=a[f].fu; int z1=get(x),z2=get(f); if(ff!=mb) { if(z1==z2) sx(f); else sx(x); } sx(x); } if(mb==0) root=x; }
几个基本操作
1.插入节点
插入的话,我觉得和权值线段树那种递归的原理差不多,遍历来找到合适的位置,加入已经有这个点就直接cnt++,如果没有的话就新建一个节点,新建之后的话把新建的点旋到根维护下树就可以了
void cr(int x) { int dq=root,f=0; while(a[dq].w!=x&&dq!=0) { f=dq; dq=a[dq].son[a[dq].w<x]; } if(dq!=0) {a[dq].js++; gx(dq);} else { dq=++num; if(f!=0) a[f].son[a[f].w<x]=dq; a[dq].size=1; a[dq].js=1; a[dq].fu=f; a[dq].w=x; } splay(dq,0); }
2.删除结点
删除还是和插入一样,有两种情况,如果这个节点的个数不为一直接cnt--,然后旋到根,如果为一的话删除这个点又不能影响其他点,但是你没办法保证删除的每一个点都没有叶子节点,这个时候就需要上旋来保证删除的点没有叶子结点,具体操作就是把前驱旋到根,后继旋到前驱下面,这样的话被删除的点就变成了叶子节点,直接清零删除就可以了
void sc(int x) { int qqq=qq(x),hjh=hj(x); splay(qqq,0); splay(hjh,qqq); int z=a[hjh].son[0]; if(a[z].js>1) {a[z].js--; gx(z); splay(z,0);} else a[hjh].son[0]=0; }
3.查询某值排名
查询排名先要找到这个值在树中的位置,当然如果没有这个值的话会一直找的叶子节点(也不一定是最接近查询值的点,我运行了一下,发现他会找到第一个比这个值小的值,而不是最接近这个数的值),这种操作的话可以搜极大值和极小值来找到树中最大值和最小值,找到这个值之后就简单了,把这个值上旋到根的位置,他左边都是比他小的,右边都是比他大的,那么他左子树的size+1就是这个值的排名
int find(int x) { int dq=root; while(a[dq].w!=x&&a[dq].son[a[dq].w<x]!=0) dq=a[dq].son[a[dq].w<x]; return dq; } int cpm(int x) { splay(find(x),0); return a[a[root].son[0]].size; }
关于find函数的运行结果(1为插入2为find查询)
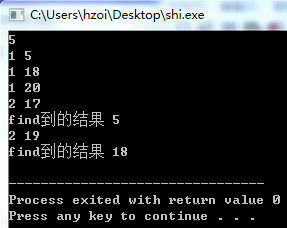
4.查询某值的前驱/后继
x的前驱:小于x的最大的数 x的后继:大于x的最小的数
用find函数查找x,把x上旋到根的位置,由于x可能不存在,而find查到的又是第一个比他小的值,所以有可能上旋后根节点就是要查询的前驱,所以要特判,但是根据我的运行结果来说,我认为后继不需要特判,如果怕不保险,特判也无所谓,反正特判应该是肯定对的那个,如果有x这个值那么前驱就是他的左子树的最右叶子节点,同理,后继就是他右子树的最左叶子节点,一直向下搜就可以了
int qq(int x) { splay(find(x),0); int dq=root; if(a[dq].w<x) return dq; dq=a[dq].son[0]; while(a[dq].son[1]!=0) dq=a[dq].son[1]; return dq; } int hj(int x) { splay(find(x),0); int dq=root; if(a[dq].w>x) return dq; dq=a[dq].son[1]; while(a[dq].son[0]!=0) dq=a[dq].son[0]; return dq; }
5.查询第k小值
跟主席树求第k小有点相似,通过记录左右子树包含的元素个数与k进行比较,选择暴力递归左儿子或者右儿子,如果当前节点的左子树元素个数小于k,那么第k小就在右子树中,k减去左子树元素个数+当前点的cnt值(还有这个元素自己)后暴力搜索右子树,如果左子树元素个数大于k,直接搜索左子树,假如k介于左子树右子树的size之间(一定要想清为什么有范围,因为同一个值可能出现多次,导致他自己代表的值就不唯一,我死在这好久),那么当前点就是第k小
int csz(int x) { int dq=root; while(1) { int ls=a[dq].son[0]; if(a[ls].size>=x) dq=ls; else if(a[ls].size+a[dq].js<x) { x-=a[ls].size+a[dq].js; dq=a[dq].son[1]; } else return a[dq].w; } }
到此,普通平衡树就可以搞定了
关于插入结点那一块,虽然最后的splay执行中会更新结点,但是我还是觉得在直接更新cnt之后更新一下节点信息比较好
现在思路是理出来了,也不知道代码能不能打下来(我依旧是个蒟蒻)
第一次完整的整理了一个知识点还有点兴奋


