DS02-栈和队列
0.展示PTA总分

1.本章学习总结
1.1 总结栈内容
- 栈是一种是一种线性表,我们只能在栈的一端进行插入和删除操作,是先进后出的一种结构。允许插入删除的一端我们称为栈顶,而另一端不允许插入删除的我们称为栈底。
- 因为栈是一种线性表,所以栈可以采用和线性表相同的存储结构:顺序存储和链式存储。顺序存储结构的栈称为顺序栈,链式存储的栈称为链栈。
- 当栈中没有数据元素时,称为空栈。栈的插入操作通常称为进栈或入栈。栈的删除操作通常称为退栈或出栈。
C++类模板:stack
头文件 #include <stack>
stack <Elemtype> s;初始化栈,保存Elemtype类型的数据
s.push(x);入栈元素t
s.top();返回栈顶指针
s.pop();出栈操作,只做删除栈顶元素的操作,不返回该删除元素
s.empty();判断是否栈空,如果为空返回true
s.size();返回栈中元素个数
栈结构定义:
/*顺序栈*/
typedef struct
{
Elemtype data[MaxSize];
int top;//栈顶指针;
}SNode;
/*链栈*/
typedef struct stack
{
Elemtype data;
struct stack* next;
}SNode,*Stack;
- 栈初始化:
/*顺序栈*/
void InitStack(SNode &s)
{
s.top=-1;//一般的顺序表栈顶指针的初始化为-1,
}
/*链栈*/
void InitStack(Stack &s)
{
s = new SNode;//申请空间;
s->next=NULL;
}
- 判断是否为空栈:
- 我们如果要访问某个地址时,一定要先判断该地址中是否已经保存了数据,否则访问就会出现错误。所以我们要先判断该栈是否是一个空栈,以保证后续访问操作的进行。
/*顺序栈*/
bool IsEmpty(SNode s)//如果为空返回true,不为空则返回false;
{
if(s.top==-1)
return true;
else
return false;
}
/*链栈*/
bool IsEmpty(Stack s)//如果为空返回true,不为空则返回false;
{
if(s->next==NULL)
return true;
else
return false;
}
- 判断是否栈满(链栈无需考虑)
- 对于顺序栈来说,是用数组来保存数据,因为数组在被定义时就需要预先申请一段连续的空间,所以如果我们要往里面进行插入的操作,必须要先判断该栈是否已经满了,否则就会出现数组溢出,访问错误的情况。
bool IsFull(sNode s)
{
if(s.top==MaxSize-1)
return true;
else
return false;
}
进栈:
/*顺序栈*/
bool Push(SNode &s,Elemtype e)
{
if(IsFull(s))//在进栈之前一定要先判断是否栈满!
return false;//返回错误;
else
s.data[++s.top] = e;
return true;//说明进栈成功;
}
/*链栈*/
void Push(Stack &s,Elemtype e)//使用头插法;
{
Stack str;
str=new Stack;
str->data = e;
str->next= s->next;//先将原来的链栈连接到str后面;
s->next = str;//再将str连接到头结点后面成为新的栈顶;
}

取栈顶元素
/*顺序栈*/
bool Gettop(SNode &s, Elemtype &e)
{
if(IsEmpty(s))//取栈顶时要判断是否为空栈!
return false;
else
e = s.data[s.top];
return true ;
}
/*链栈*/
bool Gettop(Stack &s,Elemtype &e)
{
if(IsEmpty(s))//取栈顶时要判断是否为空栈!
return false;
else
e = s->next->data;
return true;
}
出栈:
/*顺序栈*/
bool Pop(SNode &s,Elemtype &e)//出栈并返回该栈顶元素;
{
if(IsEmpty(s))//在出栈之前一定要判断是否为空栈!
return false ;//出栈错误;
else
e = s.data[s.top--];//这里只是移动了栈顶指针,并没有真正的删除数据;
return true;//出栈成功;
}
/*链栈*/
void Pop(Stack & s,Elemtype &e)
{
Stack str;
if(IsEmpty(s))//出栈之前要判断是否为空栈;
return false;
else
{
e = s->next->data;
str = s->next;
s->next = str->next;//让头结点连接栈顶的下一个结点,使s->next->next成为新的栈顶;
delete str;//释放空间,这里数据是真的被删除
}
}
销毁栈:
/*顺序栈*/
void DestroyStack(SNode &s)
{
delete s;
}
/*链栈*/
void DestroyStack(Stack &s)
{
ListStack str;
while(s!=NULL)
{
str = s;//str保存当前删除的结点
s = s->next;//s指向下一个需要删除的结点;
delete str;
}
}
栈的应用(符号配对、表达式转换、迷宫求解(回溯法))
1.以判断字符串是否是对称串为例
- 判断对称的方法,可以进行首位对比,那么就可以利用栈的特点,后进先出,将后面的元素与开始的元素进行对比
#include <iostream>
#include<stack>
using namespace std;
typedef char ElemType;
int main()
{
char str[100];
cin >> str;
char c;
stack<char>s;
int i, len;
for (i = 0; str[i] != '\n' && str[i] != '\0'; i++)
{
s.push(str[i]);
}
len = s.size();
if (len % 2 != 0)
{
cout << "no";
}
else
{
for (i = 0; i < (len / 2); i++)
{
c = s.top();
s.pop();
if (str[i] == c)
{
continue;
}
else
{
cout << "no";
return 0;
}
}
if (i == (len / 2) )
{
cout << "yes";
}
}
}
1.2 总结队列内容
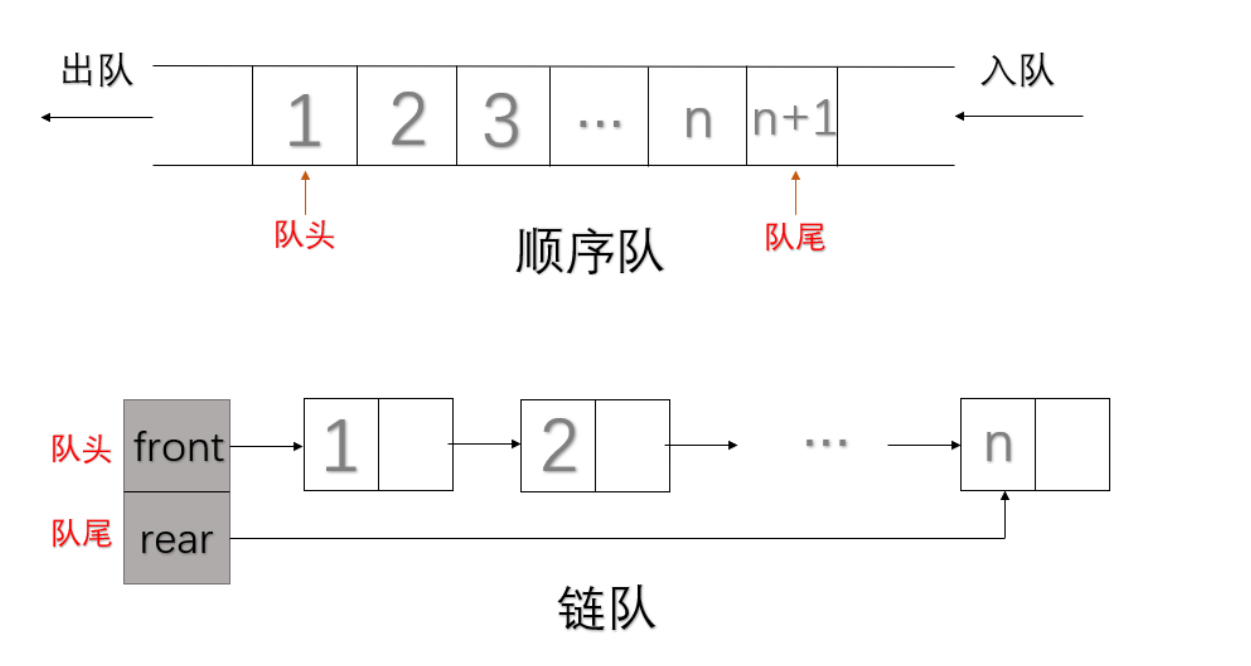
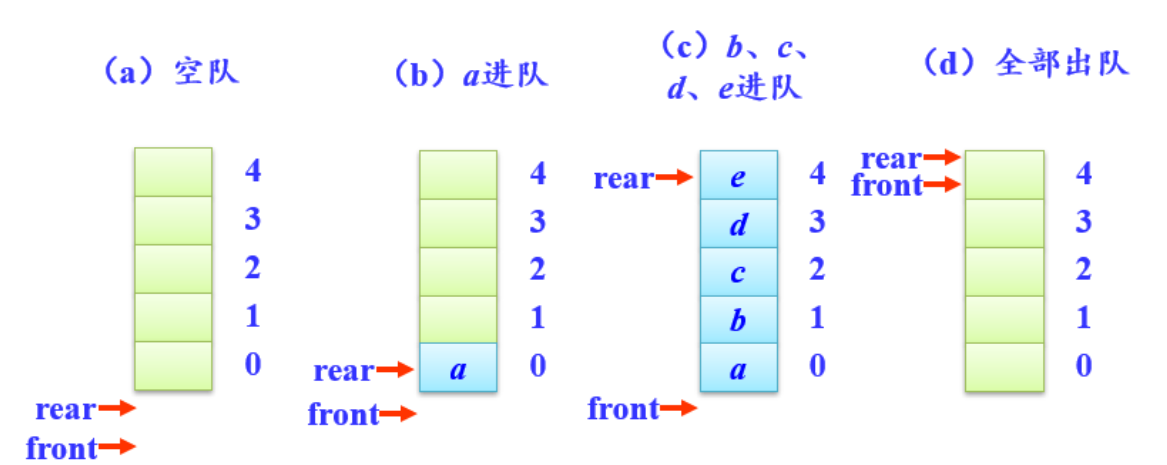
- 队列只能选取一端进行插入操作,另一端做删除操作,是先进先出的一种结构。我们把进行删除的一段叫做队头,进行插入的一端叫做队尾。
- 分为顺序存储结构和链式存储结构,顺序存储结构的队列叫做顺序队,链式存储结构的队列叫做链队。链队中,队头指针和队尾指针是单独放在一个结构体当中。
队列的定义:
/*顺序队*/
typedf struct
{
Elemtype data[MaxSize];
int front;//队头指针;
int rear;//队尾指针;
}QNode;
/*链队*/
typedef struct qnode//用于保存每个结点;
{
Elemtype data;
struct qnode *next;
}Node,*LinkNode;
typedef struct
{
LinkNode front;//队头指针;
LinkNode rear;//队尾指针;
}Queue;
队列初始化:
/*顺序队*/
void InitQueue(Queue &q)
{
q.front=q.rear=-1;
}
/*链队*/
void InitQueue(Queue &q)
{
q.front->next = NULL;
q.rear->next = NULL;
}
判断是否空
/*顺序队*/
bool IsEmpty(Queue &q)
{
if(q.rear==q.front)//队空
return true;
else//队不空
return false;
}
/*链队*/
bool IsEmpty(Queue &q)
{
if(q.front->next==NULL)//队空
return true;
else
return false;
}
队是否满(链队不需考虑)
bool IsFull(Queue &q)
{
if(q.rear==MaxSize-1)//队满
return true;
else
return false;
}
进队
/*顺序队*/
bool Push(Queue &q,Elemtype e)
{
if(IsFull(q))//在进队之前一定要先判断是否队满;
return false;//表示入队失败;
else
q.data[++q.rear] = e;
return true;//表示入队成功;
}
/*链队*/
void Push(Queue &q,Elemtype e)
{
LinkNode qtr;
qtr->data=e;
qtr->next=NULL;
if(IsEmpty(q))//先判断是否为空栈,如果为空栈要对队头指针一起修改;
q.front->next = qtr;
q.rear->next = qtr;
q.rear = qtr;
}

出队
bool Pop(Queue &q,Elemtype &e)
{
if(IsEmpty())//出栈是要先判断是否为空栈;
return false;
else
e = q.data[++q.front];
return true;//表示出队成功;
}
/*链队*/
bool Pop(Queue &q,Elentype &e)
{
LinkNode qtr;
if(IsEmpty())
return false;
else
{
qtr=q.front->next;//先用qtr保存要出队的结点;
q.front->next=qtr->next;//修改队头指针;
e = qtr->data;
delete qtr;//删除结点;
}
}
销毁队列
/*顺序栈*/
void DestroyQueue(Queue &q)
{
delete q;
}
/*链栈*/
void DestroyQueue(Queue &q)
{
LinkNode qtr;
while(q.front!=NULL)
{
qtr = q.front;//str保存当前删除的结点
q.front = q.front->next;//s指向下一个需要删除的结点;
delete qtr;
}
}
循环队列
- 当采用rear==MaxSize-1作为队满条件时,当其为真,队中可能还有若干空位置,这种溢出并不是真正的溢出,称为假溢出。
队空条件:front==rear
队满条件:(rear+1)%MaxSize==front
e进队操作:rear=(rear+1)%MaxSize //将e放在rear处
e出队操作:front=(front+1)%MaxSize //取出front处的元素e
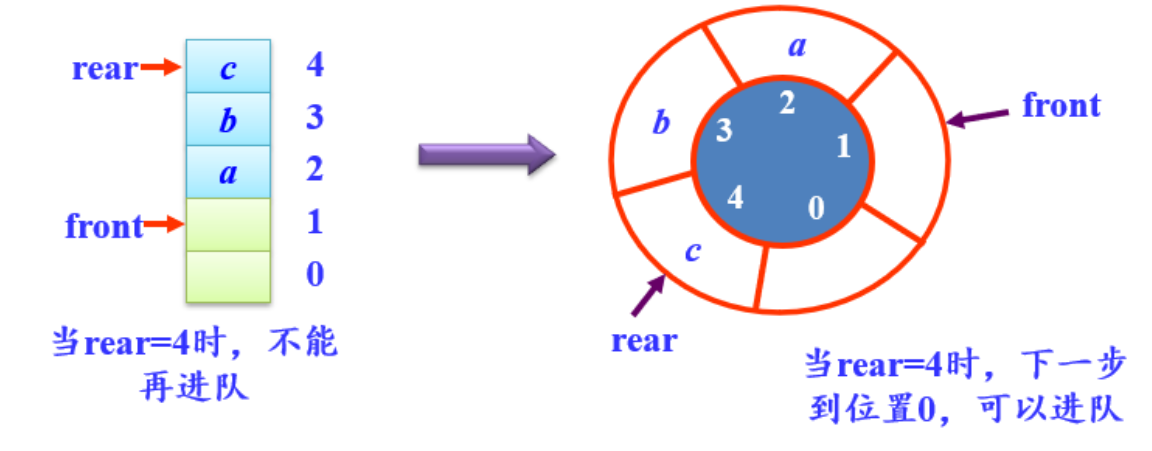
- 解决假溢出的问题,就需要把数组的前端和后端连接起来,形成一个环形的顺序表,即把存储队列元素的表从逻辑上看成一个环,称为环形队列或循环队列。
c++容器:queue
头文件:#include <queue>
q.push(x);将x插入到队列末端,成为新的队尾元素
q.pop();弹出队列的第一个元素,注意!!这里不返回被弹出元素
q.front();返回队头元素
q.back();返回队尾元素
q.empty();当队空是,返回true
q.size();返回队列的元素个数
队列应用(报数游戏、迷宫(实现最短路径))
以报数游戏为例
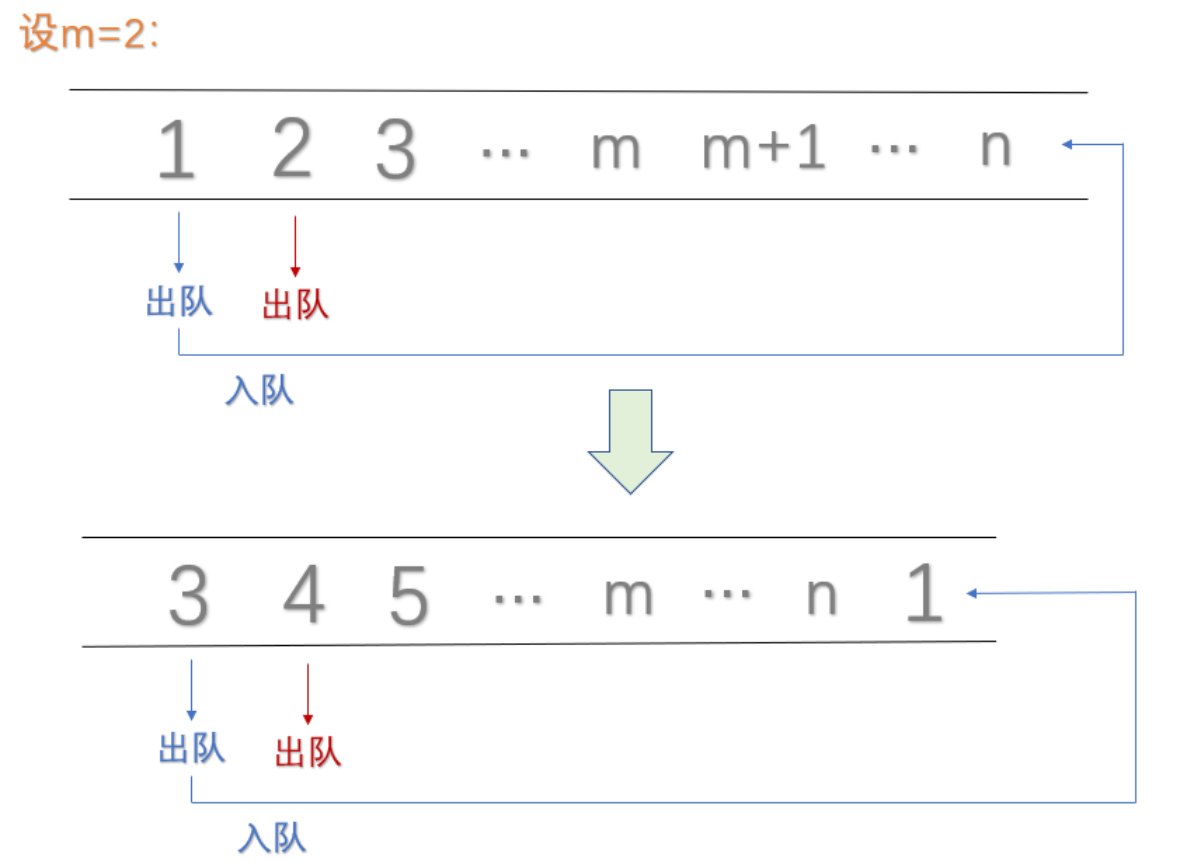
- 有n个人围成一圈,按顺序从1到n编好号。从第一个人开始报数,报到m(m<n)的人退出圈子;下一个人从1开始报数,报到m的人退出圈子。如此下去,直到留下最后一个人。其中n是初始人数;m是游戏规定的退出位次(保证为小于n的正整数)
- 代码:
#include<iostream>
#include<string>
#include<queue>
#include<map>
using namespace std;
int main()
{
int i,n,m,e,flag=1;
cin >> n;
cin >> m;
if(m>n)
{
cout<<"error!";
return 0;
}
queue<int>q;
for (i = 1; i <= n; i++)
{
q.push(i);
}
i = 1;
while (!q.empty())
{
if (i == m)
{
if (flag == 1)
{
cout << q.front();
flag++;
}
else
cout << ' ' << q.front();
q.pop();
i = 1;
}
else
{
e = q.front();
q.pop();
q.push(e);
i++;
}
}
}
1.2.对线性表的认识及学习体会
- 刚开始初步理解栈和队列时,感觉挺简单的,特别是能够使用c++容器后,代码更是简洁了很多。但是但迷宫问题出现时,我就趴下了,面对银行三兄弟更是望而却步。不过林智凯同学将这些问题简化了,等接有空还是要好好研究一下这些题目。
2.PTA实验作业
2.1 jmu-报数游戏
==========
- 报数游戏是这样的:有n个人围成一圈,按顺序从1到n编好号。从第一个人开始报数,报到m(m<n)的人退出圈子;下一个人从1开始报数,报到m的人退出圈子。如此下去,直到留下最后一个人。其中n是初始人数;m是游戏规定的退出位次(保证为小于n的正整数)。要求用队列结构完成。输出数字间以空格分隔,但结尾不能有多余空格。
- 输入样例:
5 3
- 输出样例:
3 1 5 2 4
- 输入样例:
5 6
- 输出样例:
error!
2.1.1 代码截图

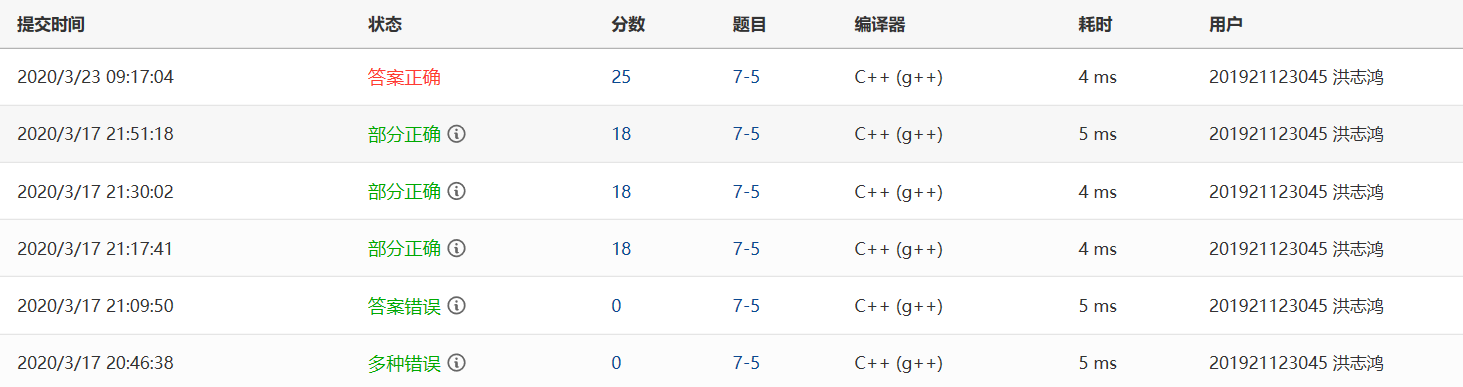
2.1.2 PTA提交列表及说明

- 先将1到n放入一个队列中,然后通过奇偶数来决定是出列或者是出列再入列
- 答案错误:没有考虑m>n的情况
2.2 表达式转换
-
算术表达式有前缀表示法、中缀表示法和后缀表示法等形式。日常使用的算术表达式是采用中缀表示法,即二元运算符位于两个运算数中间。请设计程序将中缀表达式转换为后缀表达式。
-
输入数据:
2+3*(7-4)+8/4
- 输出数据:
2 3 7 4 - * + 8 4 / +
2.2.1 代码截图

2.2.2 PTA提交列表及说明
- 多种错误,答案错误:没有考虑两位数的情况,修改完之后,得18分。
- 多种错误:还没修改小数的情况。
- 对于符号的处理,正号本是不用输出的,但是负号是要输出的,而正负号在的位置只能是左括号的右边和数字的前面,所以加个判断就好。
3.阅读代码
3.1 题目及解题代码
- 验证栈序列
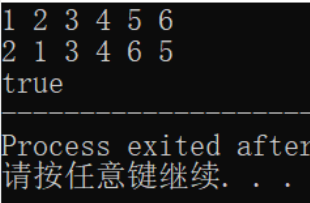
给定 pushed 和 popped 两个序列,每个序列中的 值都不重复,只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时,返回 true;否则,返回 false 。
示例一:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出:true
解释:我们可以按以下顺序执行:
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
示例二:
输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出:false
解释:1 不能在 2 之前弹出。
class Solution {
public:
bool validateStackSequences(const vector<int>& pushed, const vector<int>& popped) {
stack<int> sk;
auto first = pushed.cbegin();
for (const auto ch : popped) {
if (!sk.empty() && sk.top() == ch) {
sk.pop();
} else {
while (first != pushed.cend() && *first != ch)
sk.push(*first++);
if (first == pushed.cend()) return false;
else first++;
}
}
return first == pushed.cend();
}
};
3.1.1 该题的设计思路
遍历出栈序列,如果出栈序列合法,遍历到的符号X应该在栈的顶端,或者在入栈前的队列中。
如果在栈顶,出栈这个符号X。
不在栈顶时,遍历队列,寻找这个符号X,并将X前的符号入栈。
队列已经为空还没找到X,则出栈序列不合法。
验证完出栈序列后,判断入栈前的队列是否为空。
3.1.2 该题的伪代码
获取popped序列的大小n;
k用于遍历popped序列;
i用于遍历pushed序列;
for(i=0;i<n;i++)
{
先按照给出的进栈序列pushed[k] 按顺序进栈s;
while(!s.empty() && k<n && s.top==poped[k])//如果相等,s中的栈顶元素就出栈;
{
s.pop();
k++;//继续遍历popped的下一个元素;
}
}
判断栈是否为空,如果栈不为空,说明该出栈序列不正确;
3.1.3 运行结果
3.1.4分析该题目解题优势及难点
- 时间复杂度为:O(n)(n为序列的元素个数),最复杂的情况就是当结果为"true"时,每个元素都进栈一次又出栈一次,n个元素都进栈一次出栈一次,所以时间复杂度为O(n);
- 空间复杂度为: O(n),最坏情况是所有元素都进栈,最后再一个一个出栈,此时在栈中开辟了n个空间保存元素,空间复杂度为O(n);
3.2 题目及解题代码
- 用队列实现栈
push(x) -- 元素 x 入栈
pop() -- 移除栈顶元素
top() -- 获取栈顶元素
empty() -- 返回栈是否为空
注意:
你只能使用队列的基本操作-- 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。
你所使用的语言也许不支持队列。 你可以使用 list 或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
你可以假设所有操作都是有效的(例如, 对一个空的栈不会调用 pop 或者 top 操作)。
class MyStack {
public:
/** Initialize your data structure here. */
MyStack() {
}
/** Push element x onto stack. */
void push(int x) {
que.push(x);
for (int i = 0; i + 1 < que.size(); i++) {
que.push(que.front());
que.pop();
}
}
/** Removes the element on top of the stack and returns that element. */
int pop() {
int val = top();
que.pop();
return val;
}
/** Get the top element. */
int top() {
return que.front();
}
/** Returns whether the stack is empty. */
bool empty() {
return que.empty();
}
private:
queue<int> que;
};
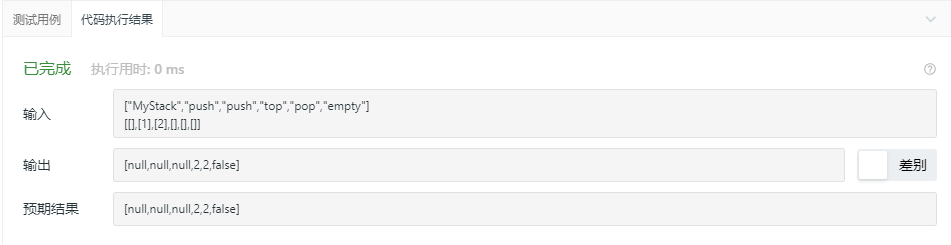
3.2.3 运行结果
3.2.4分析该题目解题优势及难点
- 入栈O(N) 出栈O(1)
- 用两个队列q1和q2,总是保持一个队列为空。
- 入栈时向非空的一个队列push;
- 出栈时,假设q1非空,则从q1队头取元素入队到q2中,直到q1中剩下一个元素,这个元素就是栈顶元素;
- 求top直接返回非空队列的队尾即可。



