DS01-线性表

0.展示PTA总分

1.本章学习总结

1.1 总结线性表内容

• 线性表是最基本、最简单、也是最常用的一种数据结构。线性表（linear list）是数据结构的一种，一个线性表是n个具有相同特性的数据元素的有限序列。即“把所有数据用一根线儿串起来，再存储到物理空间中”。
• 将数据依次存储在连续的整块物理空间中，这种存储结构称为顺序存储结构（简称顺序表）
• 结构体定义：数据类型及长度

typedef struct {
	int data[maxsize];
	int length;
}SqList;
typedef SqList* List;

• 顺序表插入

for (i = L->length - 1; i >= 0; i--)//从后面开始找插入位置，不满足元素则往后移，满足则插入
{
    if (x > L->data[i])
    {
        L->data[i + 1] = x;
        L->length++;
        return;
    }
    else
    {
        L->data[i + 1] = L->data[i];
    }
    if (i == 0)
    {
        L->data[i] = x;
        L->length++;
        return;
    }
}

• 1.先找到插入的位置 2.将数组后移 3.数组的长度增加
• 顺序表区间删除

int i,j,k;
k = 0;
j = L->length;
L->length = 0;//重构顺序表
for (i = 0; i < j; i++)
{
    if (!(L->data[i]>=min && L->data[i]<=max))//不在删除区间内的，写入重构顺序表
    {
        L->data[k++] = L->data[i];
        L->length++;
    }
}

• 数据分散的存储在物理空间中，通过一根线保存着它们之间的逻辑关系，这种存储结构称为链式存储结构（简称链表）
• 链表结构定义

typedef struct LNode        //定义单链表结点类型
{
    ElemType data;
    struct LNode *next;     //指向后继结点
} LNode,*LinkList;

• 头插法

void CreateListF(LinkList& L, int n)
{
	int i;
	LinkList node, tail;
	L = new LNode;
	tail = L;
	tail->next = NULL;
	for (i = 1; i <= n; i++)
	{
		node = new LNode;
		cin >> node->data;
		node->next = L->next;
		L->next = node;
	}

}

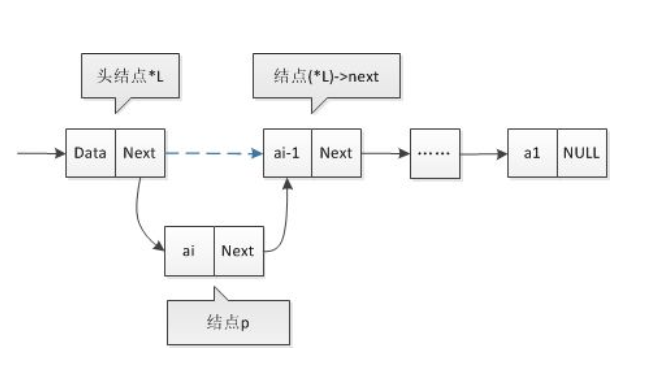
• 尾插法

void CreateListR(LinkList &L, int n)//尾插法建链表，L表示带头结点链表，n表示数据元素个数
{
    int i;
    LinkList node,tail;
    L=new LNode;
    L->next=NULL;
    tail=L;
    for(i=1;i<=n;i++)
    {
        node=new LNode;
        cin >>node->data;
        tail->next=node;
        tail=node;
    }
    tail->next=NULL;
}

• 链表插入

{
    s=new LNode;
    s->data=e;//插入节点
    s->next=p->next;
    p->next=s;
}

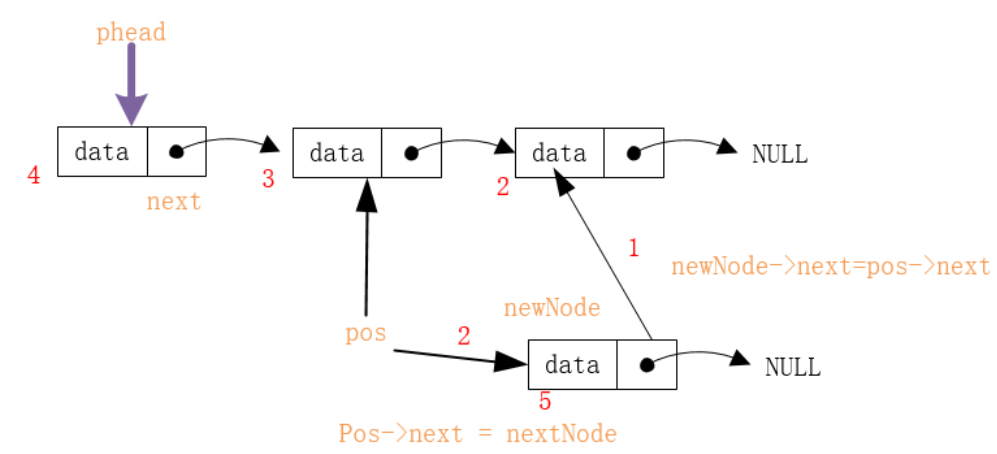
• 链表结点的删除

{
     q=p->next;//保存删除节点
     p->next=q->next;//将节点连向下一个节点
     delete q;//销毁删除节点
}

• 有序表：所有元素以递增或递减方式有序排列的线性表
• 有序表的插入

void InsertSq(SqList& L, int x)
{
	int i, j;
	int temp;
for (i = 0; i < L->length; i++)
	{
		if (x < L->data[i])
		{
			for (j = L->length ; j >i; j--)
			{
				L->data[j] = L->data[j-1];
			}
			L->data[i] = x;
			break;
		}
	}
	if (i == L->length)
	{
		L->data[i] = x;
	}
	L->length++;
}

• 有序表的合并

while (p1、p2指针都不为空)
{
if(p1数据小于p2)
		将p1数据赋给p，将p插入新链中，并移动p1指针
else if (p2数据小于p1)4
将p2数据赋给p，将p插入新链中，移动p2指针
else (即两数据相等情况)k
将p1或p2赋给p，将p插入新链中，同时移动p1, p2 
}
while (p1仍不为空)
则将L1中剩下的链接上新链
while (p2仍不为空)
则将L2中剩下的链接上新链

void MergeList(LinkList& L1, LinkList L2)//合并链表
{
	LinkList end, p1;
	p1 = L1;
	end = p1;
	L1 = L1->next;
	L2 = L2->next;
	while (L1 && L2)
	{
		if (L1->data < L2->data)
		{
			end->next = L1;
			end = L1;
			L1 = L1->next;
		}
		else if (L1->data > L2->data)
		{
			end->next = L2;
			end = L2;
			L2 = L2->next;
		}
		else
		{
			end->next = L2;
			end = L2;
			L2 = L2->next;
			L1 = L1->next;
		}
	}
	if (L1)
	{
		end->next = L1;
	}
	if (L2)
	{
		end->next = L2;
	}
    L1=p1;
}

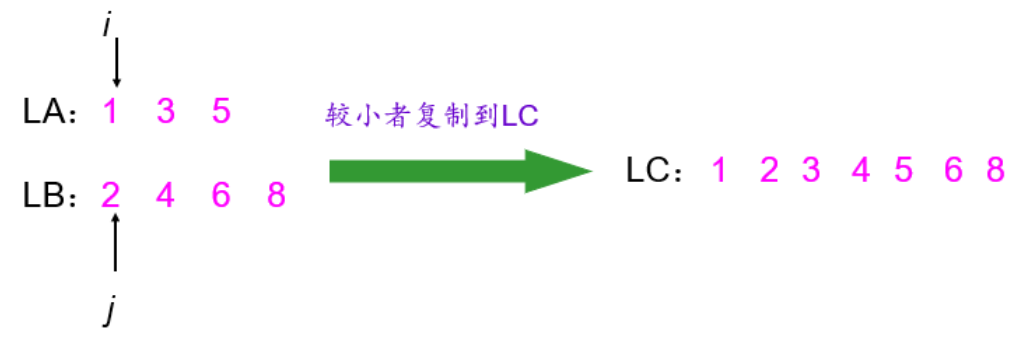
• 循环单链表是另一种形式的链式存贮结构。它的特点是表中最后一个结点的指针域指向头结点，整个链表形成一个环
• 当循环单链表为空的时候，我们可以有如下表示：
  
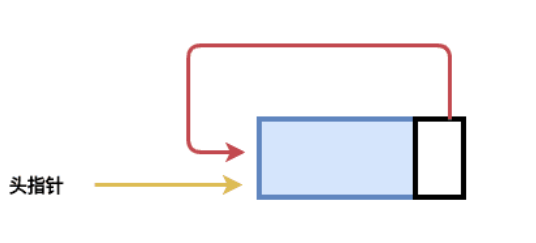
• 对于非空链表则可以这样表示：
  
• 对于循环单链表，我们在遍历的时候的结束条件就不再是p为空的时候结束了，而是p等于头结点的时候遍历才完成。
• 为了让查找更加方便，在每个节点中再多加了一个指针域，从而让一个指针域指向前一个节点，一个指针域指向后一个节点，就有了循环双链表
• 循环双链表为空时：
  
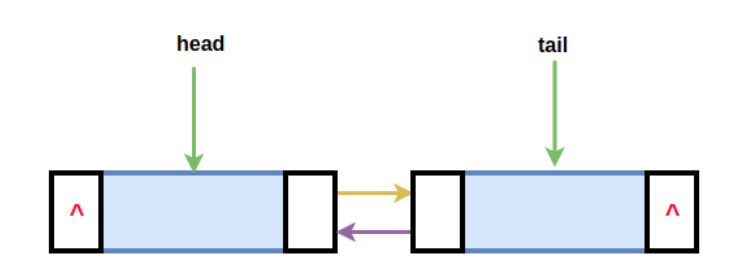
• 双向链表在初始化时，要给首尾两个节点分配内存空间。成功分配后，要将首节点的prior指针和尾节点的next指针指向NULL，这是之后用来判断空表的条件。同时，当链表为空时，要将首节点的next指向尾节点，尾节点的prior指向首节点。
• 循环双链表不为空时：
  

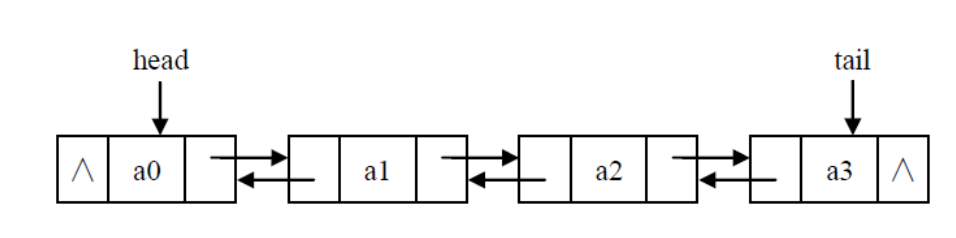
1.2.对线性表的认识及学习体会

• 上学期期末刚开始学习链表，听的都是懵的.还好这学期又重新讲了一遍，再加上pta的练习，才掌握了链表的基础操作。但是在面对判断使用p还是p->next的时候，还是比较茫然。印象深刻的是，在创建链表的时候，一定要注意最后一个节点的next是否为空。了解了线性表的结构特点和操作方式之后，可以用更高效的方法去处理以前的题目了。

2.PTA实验作业

2.1jmu-ds-链表倒数第m个数

==========

• 已知一个带有表头节点的单链表，查找链表中倒数第m个位置上的节点。
• 输入要求：先输入链表结点个数，再输入链表数据，再输入m表示倒数第m个位置。
• 输出要求，若能找到则输出相应位置，要是输入无效位置，则输出-1。
• 输入样例：

5
1 2 3 4 5
2

• 输出样例：

4

2.1.1 代码截图

2.1.2 PTA提交列表及说明

• 预习时的做法是先计算出总长度，在走总长度—m次，即可。上课时讲了更高效的做法，同时走两个指针，第一个先走m次，然后同时走，当第一个走到最后的时候，第二个恰好走到m的位置。
• 答案错误：没有考虑位置m无效的情况

2.2 jmu-ds-链表分割

• 该函数实现链表的分割。尾插法建好初始链表L={a1,b1,a2,b2,.....an,bn}。分割2个链表，其中L1和L共享头结点，分割后链表如下：
  L1:{a1,a2,...an}
  L2:
• 输入数据：

5
1 2 3 4 5

• 输出数据：

1 3 5
4 2

2.2.1 代码截图

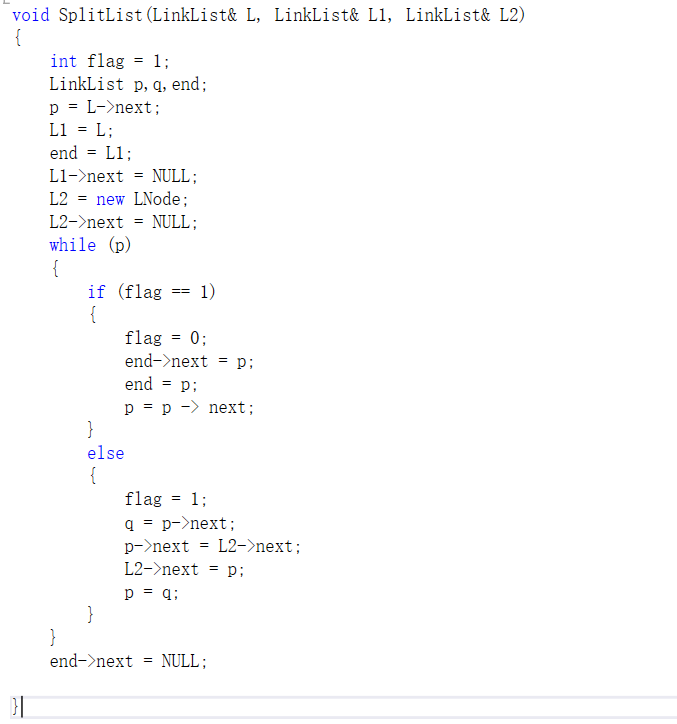
2.2.2 PTA提交列表及说明

• 做这题的时候没有想到链表的头插法。。因此做不出，后来知道了尾插头插同时使用，就顺利的做出了
• 内存超限，第一次做定义了很多指针
• 答案错误：没有审清题目，就以为是链表走一遍，一个给L1，一个给L2

2.3一元多项式的乘法与加法运算

• 设计函数分别求两个一元多项式的乘积与和。
• 输入数据：

4 3 4 -5 2  6 1  -2 0
3 5 20  -7 4  3 1

• 输出数据：

15 24 -25 22 30 21 -10 20 -21 8 35 6 -33 5 14 4 -15 3 18 2 -6 1
5 20 -4 4 -5 2 9 1 -2 0

2.3.1 代码截图

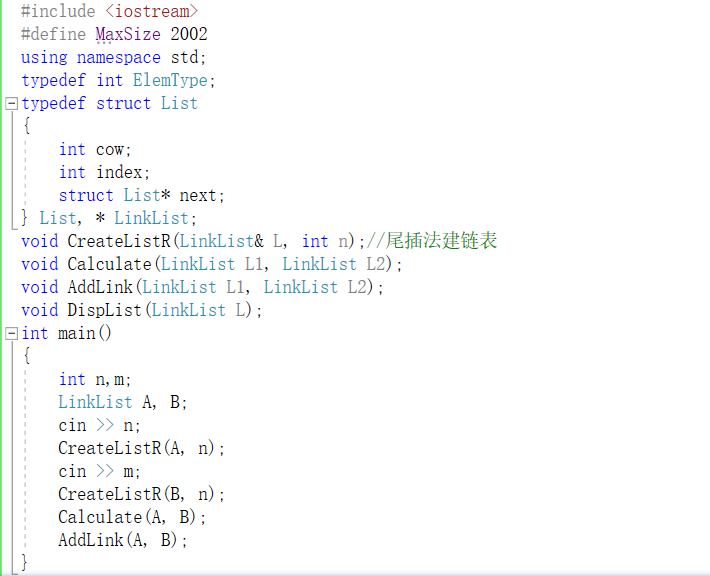
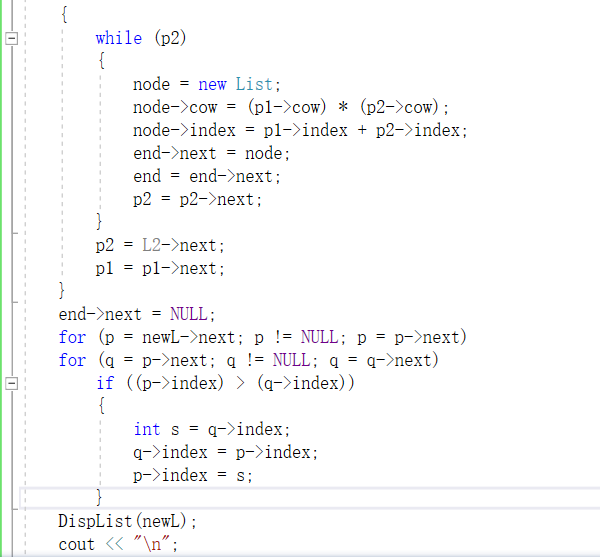
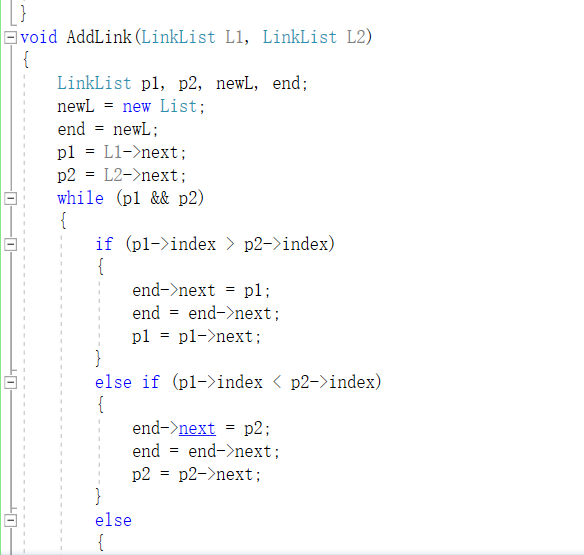
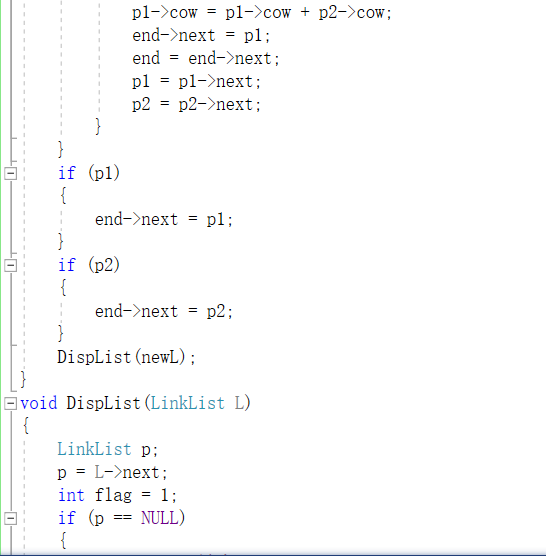
2.3.2 PTA提交列表及说明

• 答案错误：空的多项式需要用0 0输出
• 编译错误：函数没有在主函数之前定义

3.阅读代码

3.1 题目及解题代码

• 旋转链表
  给定一个链表，旋转链表，将链表每个节点向右移动 k 个位置，其中 k 是非负数。
  示例一：

输入: 1->2->3->4->5->NULL, k = 2
输出: 4->5->1->2->3->NULL
解释:
向右旋转 1 步: 5->1->2->3->4->NULL
向右旋转 2 步: 4->5->1->2->3->NULL

示例二：

输入: 0->1->2->NULL, k = 4
输出: 2->0->1->NULL
解释:
向右旋转 1 步: 2->0->1->NULL
向右旋转 2 步: 1->2->0->NULL
向右旋转 3 步: 0->1->2->NULL
向右旋转 4 步: 2->0->1->NULL

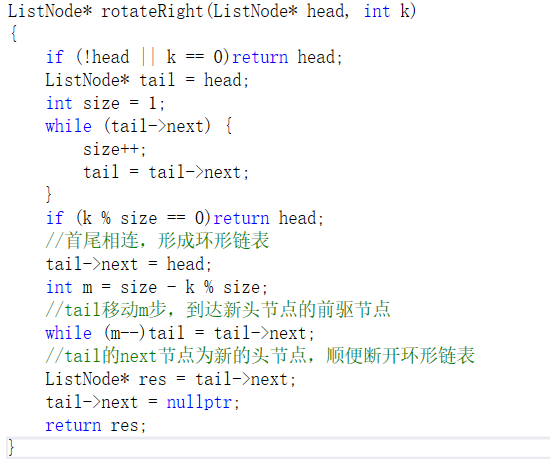
3.1.1 该题的设计思路

先求出链表长度size，若k取余size为空，那么不用旋转了，直接返回head；否则将链表首尾相连形成环形链表，由于k表示尾节点向右移动k%size位，那么头节点向右移动size-k%size位，此时的tail移动size-k%size位到达新头节点的前驱节点，我们仅仅需要保存新头节点，同时断开链表就好了。

3.1.2 该题的伪代码

if(为空链表）return 0;
while（遍历链表，记录长度）
首尾相连，形成环形链表
while(长度--)
{
     使p前进；
}
p节点为新的头节点，顺便断开环形链表

3.1.3 运行结果

3.1.4分析该题目解题优势及难点

• 看到这题时，刚开始的思路是，一个个操作节点，改变节点的值。而该题的快速解法则是：将链表变为循环链表，再改变头节点的位置，最后断开链表即可。
• 时间复杂度从O（n2）降到O（n）

3.2 题目及解题代码

• 两两交换链表中的节点
  -给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。
  实例：

给定 1->2->3->4, 你应该返回 2->1->4->3.

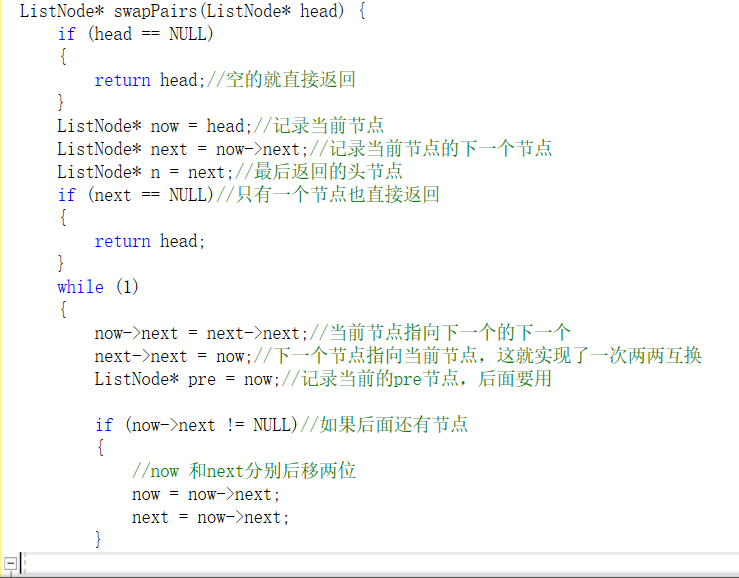
3.2.1 该题的设计思路

• 定义两个指针，同时扫描，符合条件就交换，同时将循环指针后移

3.2.2 该题的伪代码

while (1)
{
	当前节点pre指向next的下一个
		下一个节点next指向当前节点pre，这就实现了一次两两互换
		记录当前的pre节点
		if (now->next != NULL)如果后面还有节点
		{
			now 和next分别后移两位
		}
			else没有就break，这是针对节点数为偶数的情况
			if (next != NULL)如果next不是空，即节点数为偶数，此时next对应的为 2，4, 6, 8等等
				pre->next = next;
	else节点数为奇数, 则必然最后一个节点的next为空
}

3.2.3 运行结果

3.2.4分析该题目解题优势及难点

• 时间复杂度：O(N)O(N)
• 空间复杂度：O(1)O(1)
• 该题也可以采用递归的方法，写起来难度更高，但是代码相对简洁，力扣中多采用递归和该种方法，递归的时间复杂度和空间复杂度都为O（n），该法时间复杂度和空间复杂度分别为O（n）和O（1）