浅谈可持久化线段树(主席树)
Ⅰ、前言
感谢洛谷孤独·粲泽大佬写的题解,对我启发至深。
Ⅱ、预备知识
可持久化线段树,顾名思义,是建立在线段树的基础之上的,一般来说,可持久化线段树具备两种特性:
1、可以访问历史版本(即可以在之前的操作基础上询问或修改)
2、可以在历史版本的基础之上进行修改操作
明白了这些基础知识,接下来我们就可以来学习可持久化线段树了
Ⅲ、抛出问题
我们先来看一道洛谷的模板题
题目描述
如题,你需要维护这样的一个长度为\(N\)的数组,支持如下几种操作
在某个历史版本上修改某一个位置上的值
访问某个历史版本上的某一位置的值
此外,每进行一次操作(对于操作2,即为生成一个完全一样的版本,不作任何改动),就会生成一个新的版本。版本编号即为当前操作的编号(从1开始编号,版本0表示初始状态数组)
输入输出格式
输入格式:
输入的第一行包含两个正整数\(N\),\(M\)分别表示数组的长度和操作的个数。
第二行包含\(N\)个整数,依次为初始状态下数组各位的值(依次为\(a_{i}\),\(1\leq i\leq N\))。
接下来\(M\)行每行包含3或4个整数,代表两种操作之一(\(i\)为基于的历史版本号):
对于操作1,格式为\(v_{i}\) \(1\) \(loc_{i}\) \(value_{i}\), 即为在版本\(v_{i}\)的基础上,\(a_{loc_{i}}\)修改为\(value_{i}\)
对于操作2,格式为\(v_{i}\) \(2\) \(loc_{i}\),即访问版本\(v_{i}\)中的\(loc_{i}\)的值
输出格式:
输出包含若干行,依次为每个操作2的结果。
输入输出样例
输入样例#1:
5 10
59 46 14 87 41
0 2 1
0 1 1 14
0 1 1 57
0 1 1 88
4 2 4
0 2 5
0 2 4
4 2 1
2 2 2
1 1 5 91
输出样例#1:
59
87
41
87
88
46
说明:
\(1\leq N,M\leq10^6\)
Ⅳ、分析问题
可持久化线段树,其特点在于,可以访问历史版本的值(上面讲了),那么如何记录历史版本呢?
最朴素的思想就是,我们每遇到一次操作,就把上次的线段树复制下来,再在复制后的线段树上进行操作,相当于每有一次操作,就新建一个线段树,并记录每棵线段树的根节点编号,每次访问时访问某棵线段树即可。
可仔细分析复杂度后,发现时间复杂度远大于正常范围,空间更是开不下,直接新建新线段树这个方法算是废了,能不能在原来的基础上改进呢?
分析下图,第0棵线段树(红色为点权值,绿色为其覆盖区间)

第1棵线段树是下图↓

我们发现,第一棵线段树与初始线段树(我们暂且在这里怎么称呼它)几乎一模一样,如果把原来的节点都复制一遍,相当于多开了许多空间,而初始线段树的节点权却没有发挥作用。
怎么解决呢?
这里引入一个新操作,可能我们的新线段树可以和历史版本的线段树共用一段空间,因为每次线段树的改动是极为微小的,只改动了\(\log_{2}{n}\)的节点,剩下的节点并没有修改,此时我们即可将未改动部分和历史版本的这一部分共用一段空间
如图,第1棵线段树与第0棵线段树共用了2~9这一段空间,在节点数量非常多的情况下,这个操作能取得很明显的效果。

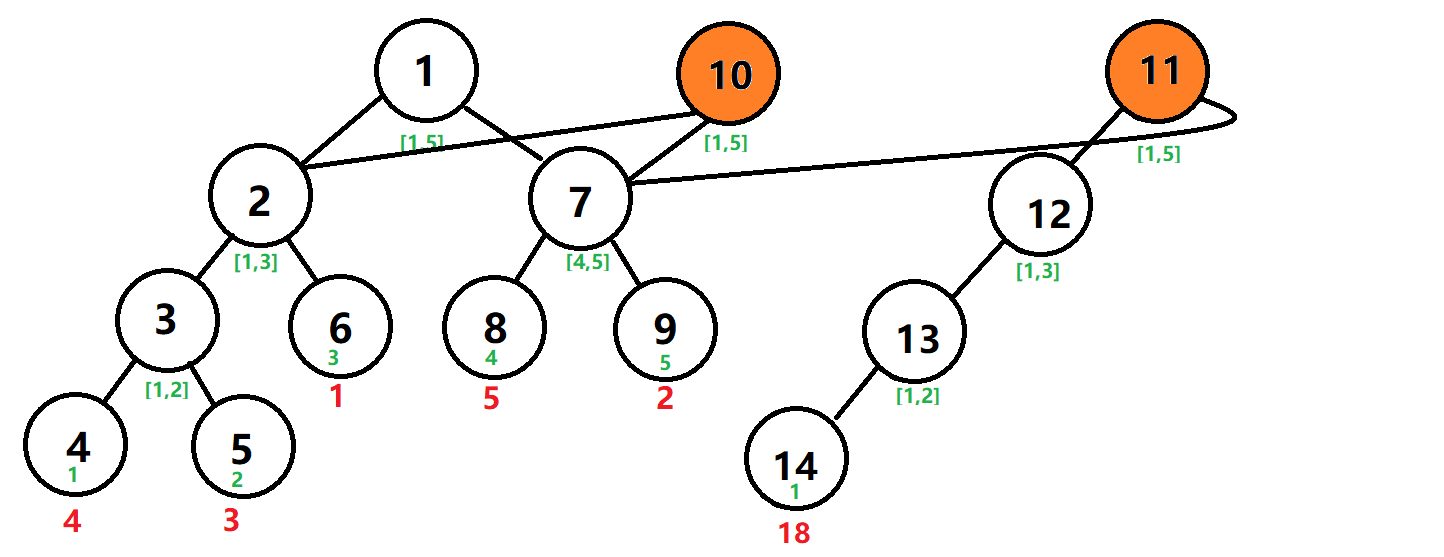
第二次操作,将一号节点的值加14
接下来就是代码(下面有详细的注释哦):
#include<bits/stdc++.h>
#define ll long long
#define INF 2147483647
#define mem(i,j) memset(i,j,sizeof(i))
#define F(i,j,n) for(register int i=j;i<=n;i++)
using namespace std;
int n,m,pntnum=0;//pntnum表示一共建立过多少点
int v[20000010],root[20000010];//v为输入的点权,root[i]表示第i棵线段树的根节点
inline int read(){//快读没有什么问题
int datta=0;char chchc=getchar();bool okoko=0;
while(chchc<'0'||chchc>'9'){if(chchc=='-')okoko=1;chchc=getchar();}
while(chchc>='0'&&chchc<='9'){datta=datta*10+chchc-'0';chchc=getchar();}
if(okoko==1)return -datta;return datta;
}
struct Persistable_Segment_Tree{
int ls[20000010],rs[20000010],tree[20000010];
//ls[i]为i的左儿子,rs[i]为i的右儿子,tree[i]为i的值
void build_tree(int &pos,int l,int r){
pos=++pntnum;//添加新节点,当前节点编号为++pntnum
if(l==r){
tree[pos]=v[l];//初始化每个叶节点的值
return ;
}
int mid=(l+r)>>1;
build_tree(ls[pos],l,mid);
build_tree(rs[pos],mid+1,r);
}
void add(int &pos,int vsn,int l,int r,int loc,int val){//pos新版本的当前节点编号,vsn旧版本的当前节点编号,l左端点,r右端点,loc要修改的节点编号,val修改值
pos=++pntnum;//新建节点
if(l==r){
tree[pos]=val;//修改值
return ;
}
ls[pos]=ls[vsn];//继承旧版本左子树
rs[pos]=rs[vsn];//继承旧版右左子树
int mid=(l+r)>>1;
if(loc<=mid)//如果要修改的节点在左子树中
add(ls[pos],ls[vsn],l,mid,loc,val);//处理左子树
else
add(rs[pos],rs[vsn],mid+1,r,loc,val);//处理右子树
}
int ask(int vsn,int l,int r,int loc){//vsn要访问的版本的当前节点编号,l左端点,r右端点,loc要访问的节点编号
if(l==r)
return tree[vsn];
int mid=(l+r)>>1;
if(loc<=mid)//如果在左子树中
return ask(ls[vsn],l,mid,loc);
else
return ask(rs[vsn],mid+1,r,loc);
}
}T;
int main(){
n=read();m=read();
F(i,1,n)
v[i]=read();
T.build_tree(root[0],1,n);//建树
F(i,1,m){
int rt=read(),kd=read(),loc=read(),val;//rt历史版本编号,kd操作类型,loc节点编号,val修改后的值
if(kd==1){
val=read();
T.add(root[i],root[rt],1,n,loc,val);
}else{
root[i]=root[rt];//root[i]是第i个版本的根节点编号,因为没有修改,所以只需要继承以前版本
printf("%d\n",T.ask(root[rt],1,n,loc));
}
}
return 0;
}
区间第k小是可持久化线段树的一个经典应用,如题
题目描述
如题,给定\(N\)个正整数构成的序列,将对于指定的闭区间查询其区间内的第\(k\)小值。
输入输出格式
输入格式:
第一行包含两个正整数\(N\)、\(M\),分别表示序列的长度和查询的个数。
第二行包含\(N\)个正整数,表示这个序列各项的数字。
接下来M行每行包含三个整数\(l,r,k\),表示查询区间\(\left[l,r\right]\)内的第\(k\)小值。
输出格式:
输出包含\(k\)行,每行1个正整数,依次表示每一次查询的结果
输入输出样例
输入样例#1:
5 5
25957 6405 15770 26287 26465
2 2 1
3 4 1
4 5 1
1 2 2
4 4 1
输出样例#1:
6405
15770
26287
25957
26287
区间第k小问题可以有许多其他写法,我们这里尝试使用可持久化线段树解题。
区间第k小(无修改操作):
#include<bits/stdc++.h>
#define ll long long
#define mem(i,j) memset(i,j,sizeof(i))
#define F(i,j,n) for(register int i=j;i<=n;i++)
using namespace std;
struct hahaha{
int v,id;
}s[4000010];
int n,m,pntnum=0,a[4000010];
int root[4000010],b[4000010];
inline int read(){
int datta=0;char chchc=getchar();bool okoko=0;
while(chchc<'0'||chchc>'9'){if(chchc=='-')okoko=1;chchc=getchar();}
while(chchc>='0'&&chchc<='9'){datta=datta*10+chchc-'0';chchc=getchar();}
if(okoko==1)return -datta;return datta;
}
inline bool cmp(hahaha a,hahaha b){
return a.v<b.v;
}
struct Persistable_Segment_Tree{
int ls[4000010],rs[4000010],tree[4000010];
void build_tree(int &pos,int l,int r){
pos=++pntnum;
if(l==r)
return ;
int mid=(l+r)>>1;
build_tree(ls[pos],l,mid);
build_tree(rs[pos],mid+1,r);
}
void add(int &pos,int vsn,int l,int r,int loc){//pos新版本的当前节点编号,vsn旧版本的当前节点编号,l左端点,r右端点,loc要修改的节点编号
pos=++pntnum;
if(l==r){
tree[pos]=tree[vsn]+1;//当前节点加1
return ;
}
ls[pos]=ls[vsn];//继承左子树
rs[pos]=rs[vsn];//继承右子树
tree[pos]=tree[vsn]+1;//当前路径上的所有点权值加1
int mid=(l+r)>>1;
if(loc<=mid)
add(ls[pos],ls[vsn],l,mid,loc);
else
add(rs[pos],rs[vsn],mid+1,r,loc);
}
int ask(int lv,int rv,int l,int r,int k){
if(l==r)
return l;//返回第l小
int mid=(l+r)>>1,sum=tree[ls[rv]]-tree[ls[lv]];//sum为第rv棵树的
if(k<=sum)
return ask(ls[lv],ls[rv],l,mid,k);
else
return ask(rs[lv],rs[rv],mid+1,r,k-sum);
}
}T;
int main(){
n=read();m=read();
F(i,1,n)
s[i].v=read(),s[i].id=i;
sort(s+1,s+n+1,cmp);//将节点按权值排序
int num=0;
s[0].v=-0x3f3f3f3f;
F(i,1,n)
a[s[i].id]=(s[i].v!=s[i-1].v)?++num:num;//将节点权值离散化
int nowi=1,numi=1;
while(numi<=n){
if(s[numi].v!=s[numi-1].v)
b[nowi++]=s[numi].v;//将离散化后的数组每个数只出现一次地放到b数组中,便于最后输出第几小
numi++;
}
T.build_tree(root[0],1,nowi);//建空树
F(i,1,n)
T.add(root[i],root[i-1],1,n,a[i]);//加点,详见add函数
F(i,1,m){
int lft=read(),rht=read(),kn=read();
printf("%d\n",b[T.ask(root[lft-1],root[rht],1,n,kn)]);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号