浅谈斜率优化dp
Ⅰ、前置知识
\(y=kx+b\)
\(k\)叫斜率,\(b\)叫截距
\((x_1,y_1)\)\((x_2,y_2)\)两点连成的直线的斜率\(k=\frac{y1-y2}{x1-x2}\)
Ⅱ、抛出问题
洛谷板子
题目描述
\(n\)个任务排成一个序列在一台机器上等待完成(顺序不得改变),这\(n\)个任务被分成若干批,每批包含相邻的若干任务。从时刻\(0\)开始,这些任务被分批加工,第\(i\)个任务单独完成所需的时间是\(T_i\)。在每批任务开始前,机器需要启动时间\(S\),而完成这批任务所需的时间是各个任务需要时间的总和(同一批任务将在同一时刻完成)。每个任务的费用是它的完成时刻乘以一个费用系数\(F_i\)。请确定一个分组方案,使得总费用最小。
例如:\(S=1\);\(T=\{1,3,4,2,1\}\);\(F=\{3,2,3,3,4\}\)。如果分组方案是\(\{1,2\}\)、\(\{3\}\)、\(\{4,5\}\),则完成时间分别为\(\{5,5,10,14,14\}\),费用\(C=\{15,10,30,42,56\}\),总费用就是\(153\)。
输入输出格式
输入格式:
第一行是\(n(1\leq n\leq5000)\)。
第二行是\(S(0\leq S\leq50)\)。
下面\(n\)行每行有一对数,分别为\(T_i\)和\(F_i\),均为不大于\(100\)的正整数,表示第\(i\)个任务单独完成所需的时间是\(T_i\)及其费用系数\(F_i\)。
输出格式:
一个数,最小的总费用。
输入输出样例
输入样例#1:
5
1
1 3
3 2
4 3
2 3
1 4
输出样例#1:
153
Ⅲ、分析问题
首先这题\(O(n^2)\)可以艹过
但是\(O(n^2)\)过了这题讲斜率优化毫无意义QAQ
所以请自动将数据范围改成\((1\leq n\leq500000)\)
先来看一眼普通\(dp\)\(O(n^2)\)怎么写
设
\(f[i]\)表示处理到第\(i\)个任务,前\(i\)个的最小费用
\(t_i\)表示时间的前缀和
\(c_i\)表示费用的前缀和
考虑从\(j\)转移到\(i\),表示\(j+1\)到\(i\)打包到一批
则状态转移方程为
由于之前哪些任务被分成一批不好处理,所以可以直接加上\(s\times(c_n-c_j)\)当作对后续状态的处理
然后推式子
将\(j\)看作一个变量,然后去掉\(\min\),得到
拆括号
移项
提取公因式
此时式子推成这样
再看一眼前置知识
\(y=kx+b?\)
此时我们的式子就像一条直线解析式!
我们想要最小化\(f[i]\),就是最小化\(b\)
而我们此时要做的,就是用一条已知斜率的直线,利用已有的坐标,找到一个最小的\(b\)
如图,现在处理到\(i\),则共有\(i-1\)个坐标为\((z_j,f[j])(1\leq j<i)\)的点
如图所示
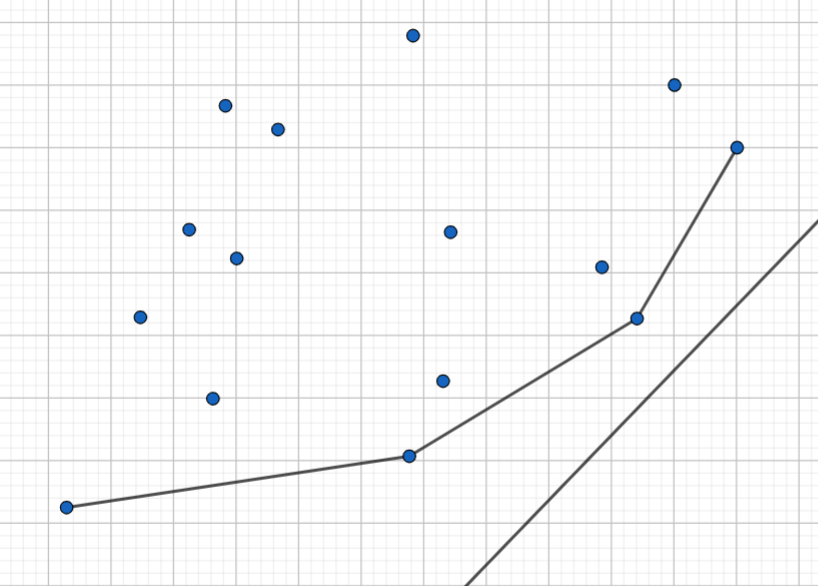
右下角为当前处理的斜率为\(s+t_i\)的直线,我们要将它向上平移,直到和上方\(i-1\)个点中的一个相交
显然要找的点\(j\)(也叫决策点)一定在图形的凸包上
又很显然,决策点一定在下凸壳上,因为下凸壳上的点显然比上凸壳更优
又很显然,决策点一定在下凸壳的右半侧,因为\(k\)(即\(s+t_i\))一定大于\(0\)
叕很显然找到决策点之后是这样的
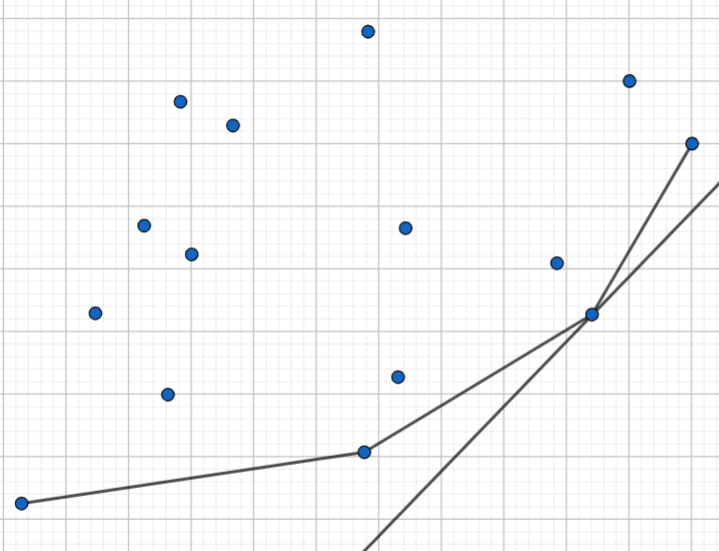
如何找到决策点?
观察可以知道,凸包上的直线的斜率具有单调性
二分!
每次二分一个点,\(check\)这个点左侧的直线的斜率是否小于\(s+t_i\),右侧的斜率是否大于\(s+t_i\),如果是就证明找到了决策点
手玩一下更好理解
找到决策点之后,很明显,决策点左边所有的直线的截距都要大于\(s+t_i\),所以左边的所有点都没有当前点优
于是拿单调队列存一下凸包是上的点,如果没有当前直线优则踢掉
找到决策点后,相当于找到了\(j\),更新\(f[i]\)
更新完\(f[i]\)后,为了方便后续的查找,将\((c_i,f[i])\)插入凸包,并且维护一下凸包的单调性
最后输出\(f[n]\)即可
代码:
#include<bits/stdc++.h>
#define F(i,j,n) for(register int i=j;i<=n;i++)
#define INF 0x3f3f3f3f
#define ll long long
#define mem(i,j) memset(i,j,sizeof(i))
using namespace std;
int n,s,c[5010],t[5010],f[5010],q[5010],l,r;
inline int read(){
int datta=0;char chchc=getchar();bool okoko=0;
while(chchc<'0'||chchc>'9'){if(chchc=='-')okoko=1;chchc=getchar();}
while(chchc>='0'&&chchc<='9'){datta=datta*10+chchc-'0';chchc=getchar();}
return okoko?-datta:datta;
}
int main(){
n=read();s=read();
F(i,1,n){
t[i]=t[i-1]+read();
c[i]=c[i-1]+read();
}
mem(f,0x3f);
f[0]=0;
l=1;r=0;
q[++r]=0;
F(i,1,n){
while(l<r&&f[q[l+1]]-f[q[l]]<=(s+t[i])*(c[q[l+1]]-c[q[l]]))//避免精度误差
l++;//由于博主太菜了所以用的是线性而不是二分
f[i]=f[q[l]]+s*(c[n]-c[q[l]])+t[i]*(c[i]-c[q[l]]);//更新
while(l<r&&(f[i]-f[q[r]])*(c[q[r]]-c[q[r-1]])<=(f[q[r]]-f[q[r-1]])*(c[i]-c[q[r]]))
r--;
q[++r]=i;
}
printf("%d\n",f[n]);
return 0;
}


