浅谈树链剖分

Ⅰ、预备知识

树链剖分，又叫重链剖分，树剖。顾名思义，就是在树上将树划分为一条条链，然后进行树上修改与查询操作(针对于结点操作，边权操作后面会讲)，用数据结构来维护保证时间复杂度(数据结构模板)，本篇文章中以线段树为例说明。一般来说，可以支持以下几种操作：
1、树上路径区间修改
2、树上路径间的区间查询(如点权之和，最大值等)
讲道理实际上线段树能做的它在树上都能做QAQ
接下来进入毒瘤内容

Ⅱ、抛出问题

先看一道板子

题目描述

如题，已知一棵包含N个结点的树（连通且无环），每个节点上包含一个数值，需要支持以下操作：
操作1：格式：1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2：格式：2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3：格式：3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4：格式：4 x 表示求以x为根节点的子树内所有节点值之和

输入输出格式

输入格式：

第一行包含4个正整数N、M、R、P，分别表示树的结点个数、操作个数、根节点序号和取模数（即所有的输出结果均对此取模）。
接下来一行包含N个非负整数，分别依次表示各个节点上初始的数值。
接下来N-1行每行包含两个整数x、y，表示点x和点y之间连有一条边（保证无环且连通）
接下来M行每行包含若干个正整数，每行表示一个操作，格式如下：
操作1： 1 x y z
操作2： 2 x y
操作3： 3 x z
操作4： 4 x

输出格式：

输出包含若干行，分别依次表示每个操作2或操作4所得的结果（对P取模）

输入输出样例

输入样例#1：

5 5 2 24
7 3 7 8 0
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3

输出样例#1：

2
21

说明：

时空限制：1s，128M
数据规模：
对于30%的数据：\(N\leq 10,M\leq 10\)
对于70%的数据：\(N\leq{10}^3,M\leq{10}^3\)
对于100%的数据：\(N\leq{10}^5,M\leq{10}^5\)
（其实，纯随机生成的树LCA+暴力是能过的，可是，你觉得可能是纯随机的么233）
样例说明：
树的结构如下：

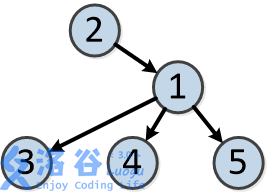
各个操作如下：

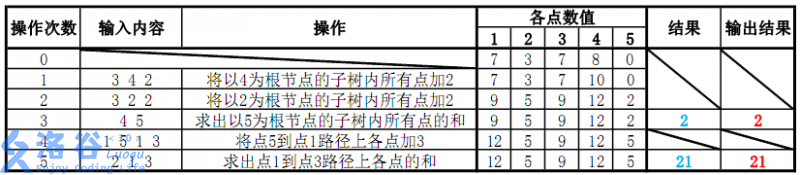
故输出应依次为2、21(重要的事情说三遍：记得取模)

Ⅲ、分析问题

先把几个概念弄明白：

sz[u] 子树u的大小，包括u本身
dep[u] 结点u的深度，根节点深度为1
重儿子 节点u的子树中，sz最大的那个子树的根，用son[u]表示(叶结点无重儿子)
重链 由连接结点与其重儿子的边连接而成的路径(单独的结点也是一条重链)
轻链 又叫轻边，树中除了重链剩下的边
top[u] 结点u所在重链dep最小的结点(也就是最上面的点)
id[u] 树上结点u在线段树中的编号

原谅我语文不好。。。
放张图吧QAQ

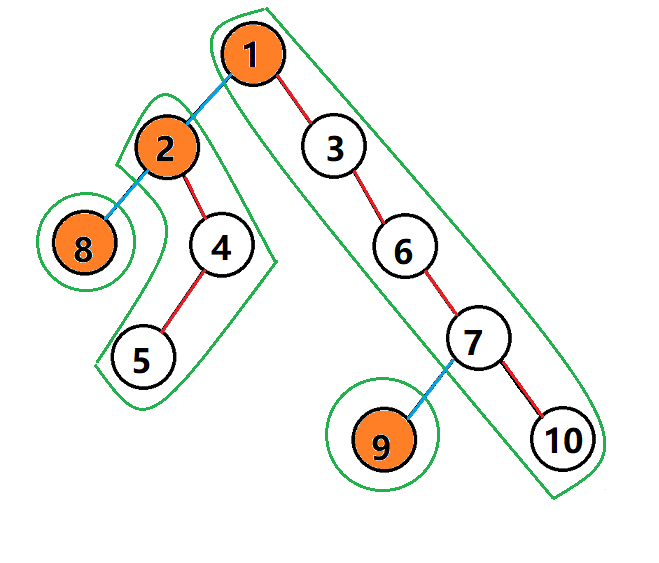
画的真帅
如图绿色框起来的是重链，橙色的是top，红的边是重链里的边，蓝的是轻边，可以发现轻边连接两条重链
举个栗子：

top[8]=8;top[7]=1;top[5]=2;son[1]=2;son[2]=8;son[6]=7;sz[2]=4;

预处理code:

inline ll dfs1(ll from){
    ll tmp=0,tmx=0,ti=0;
    for(ll i=head[from];i;i=s[i].nxt){
        ll to=s[i].to;
        if(to!=f[from]){
            dep[to]=dep[from]+1;//处理dep
            f[to]=from;//处理fa
            tmp=dfs1(to);
            sz[from]+=tmp;//处理sz
            if(tmp>tmx)//处理重儿子
                tmx=tmp,ti=to;
        }
    }
    sz[from]++;
    son[from]=ti;
    return sz[from];
}
inline void dfs2(ll from,ll tp){
    id[from]=++num,vt[num]=v[from];//处理id和线段树上初始点权
    if(son[from])
        top[son[from]]=tp,dfs2(son[from],tp);//先递归处理重儿子，使得重链编号连在一起
    for(ll i=head[from];i;i=s[i].nxt){
        ll to=s[i].to;
        if(to!=f[from]&&to!=son[from])
            top[to]=to,dfs2(to,to);//递归处理轻儿子
    }
}

预处理好了，那么如何在树链上进行更改操作呢？
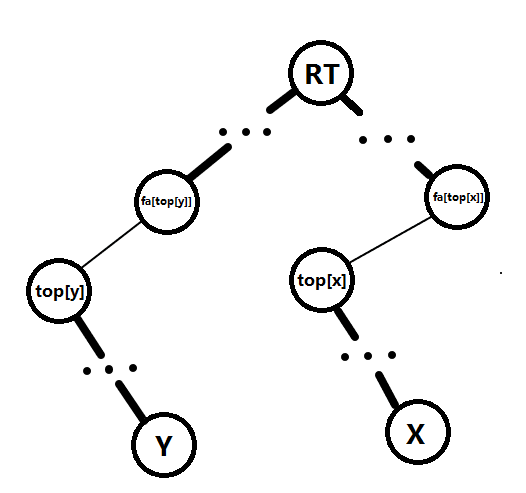
如图，先看一种特殊情况，将x到y的路径全部加k(y为x祖先结点)

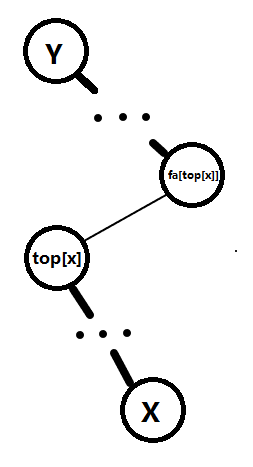
如上图，x->top[x]的路径是一条重链，top[x]->fa[top[x]]是一条轻边，fa[top[x]]->y的路径是一条重链。
将x到y区间加，很显然就是先将x到top[x]在线段树上区间加k，然后在将fa[top[x]]到y在线段树上加k。
代码如下(实际上这一段并没有什么luan用)
Code:

void cRange(int x,int y,int k){//区间修改
    while(top[x]!top[y]){//不在同一条重链上
        S.change(1,1,n,id[top[x]],id[x],k);//线段树上区间加k
        x=fa[top[x]];//将x变为fa[top[x]]
    }
    S.change(1,1,n,id[y],id[x],k);//将x到y区间加
}

询问也类似于区间加，只是多记录个res

int qRange(int x,int y,int k){//区间查询
    int res=0;
    while(top[x]!top[y]){//不在同一条重链上
        res+=S.ask(1,1,n,id[top[x]],id[x],k);//查询x到top[x]
        res%=md;
        x=fa[top[x]];//将x变为fa[top[x]]
    }
    res+=S.change(1,1,n,id[y],id[x],k);//查询x到y
    return res%md;
}

讨论第二种情况:x与y不在同一条链上(注：这里不是指重链)

考虑类似倍增的方法，将x与y不断往上跳，直到在同一条重链上为止
1、比较x、y top的大小，将x的top置为dep较大的那个
2、在线段树上处理x至其top结点
3、将x置为fa[top[x]]
4、如果x、y不在同一条重链上，返回1
5、处理区间x至y
详见代码:
Code:

inline void cRange(int x,int y,int z){
	while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]])
			swap(x,y);
		T.change(1,1,n,id[top[x]],id[x],z);
		x=f[top[x]];
	}
	if(dep[x]<dep[y])
		swap(x,y);
	T.change(1,1,n,id[y],id[x],z);
}
inline int qRange(int x,int y){
	int res=0;
	while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]])
			swap(x,y);
		res+=T.ask(1,1,n,id[top[x]],id[x]);
		res%=md;
		x=f[top[x]];
	}
	if(dep[x]<dep[y])
		swap(x,y);
	res+=T.ask(1,1,n,id[y],id[x]);
	return res%md;
}

然而还有两种操作，对树的修改与查询，如何解决？
显然，可以发现，对于树上任意一棵子树来说，它们在线段树上的编号(即id)是连在一起的(废话)
于是，很显然，对于树的操作可以这么写：

inline void cTree(int x,int z){
	T.change(1,1,n,id[x],id[x]+sz[x]-1,z);
}
inline int qTree(int x){
	return T.ask(1,1,n,id[x],id[x]+sz[x]-1)%md;
}

至此，树链剖分的模板就搞定了，下面是代码：

#include<bits/stdc++.h>
#define ll long long
#define INF 2147483647
#define mem(i,j) memset(i,j,sizeof(i))
#define F(i,j,n) for(register int i=j;i<=n;i++)
#define md p
using namespace std;
struct hahaha{
	int from,to,nxt;
}s[200010];
int n,m,r,p,head[200010],cnt=0,pls[1000010];
int v[100010],f[100010],son[100010];
int dep[100010],top[100010],sz[100010];
int id[1000010],vt[1000010],num=0;
inline int read(){
	int datta=0;char chchc=getchar();bool okoko=0;
	while(chchc<'0'||chchc>'9'){if(chchc=='-')okoko=1;chchc=getchar();}
	while(chchc>='0'&&chchc<='9'){datta=datta*10+chchc-'0';chchc=getchar();}
	if(okoko==1)return -datta;
	return datta;
}
inline void ins(int from,int to){
	s[++cnt].from=from;
	s[cnt].to=to;
	s[cnt].nxt=head[from];
	head[from]=cnt;
}
inline int dfs1(int from){
	int tmp=0,tmx=0,ti=0;
	for(int i=head[from];i;i=s[i].nxt){
		int to=s[i].to;
		if(to!=f[from]){
			dep[to]=dep[from]+1;
			f[to]=from;
			tmp=dfs1(to);
			sz[from]+=tmp;
			if(tmp>tmx)
				tmx=tmp,ti=to;
		}
	}
	sz[from]++;
	son[from]=ti;
	return sz[from];
}
inline void dfs2(int from,int tp){
	id[from]=++num,vt[num]=v[from];
	if(son[from])
		top[son[from]]=tp,dfs2(son[from],tp);
	for(int i=head[from];i;i=s[i].nxt){
		int to=s[i].to;
		if(to!=f[from]&&to!=son[from])
			top[to]=to,dfs2(to,to);
	}
}
struct Segment_Tree{
	#define ls u<<1
	#define rs u<<1|1
	#define mid ((l+r)>>1)
	int tree[1000010];
	void updata(int u){
		tree[u]=(tree[ls]+tree[rs])%md;
	}
	void pushdown(int u,int l,int r){
		if(!pls[u])
			return ;
		pls[ls]+=pls[u];
		pls[rs]+=pls[u];
		tree[ls]+=(mid-l+1)*(pls[u]);
		tree[rs]+=(r-mid)*(pls[u]);
		pls[u]=0;
	}
	void build_tree(int u,int l,int r){
		if(l==r){
			tree[u]=vt[l];
			return ;
		}
		build_tree(ls,l,mid);
		build_tree(rs,mid+1,r);
		updata(u);
	}
	void change(int u,int l,int r,int x,int y,int z){
		if(x<=l&&r<=y){
			pls[u]+=z;
			tree[u]+=(r-l+1)*z;
			return ;
		}
		pushdown(u,l,r);
		if(x<=mid)
			change(ls,l,mid,x,y,z);
		if(y>=mid+1)
			change(rs,mid+1,r,x,y,z);
		updata(u);
	}
	int ask(int u,int l,int r,int x,int y){
		int res=0;
		if(x<=l&&r<=y)
			return tree[u];
		pushdown(u,l,r);;
		if(x<=mid)
			res+=ask(ls,l,mid,x,y);
		if(y>=mid+1)
			res+=ask(rs,mid+1,r,x,y);
		return res;
	}
}T;
inline void cRange(int x,int y,int z){
	while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]])
			swap(x,y);
		T.change(1,1,n,id[top[x]],id[x],z);
		x=f[top[x]];
	}
	if(dep[x]<dep[y])
		swap(x,y);
	T.change(1,1,n,id[y],id[x],z);
}
inline int qRange(int x,int y){
	int res=0;
	while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]])
			swap(x,y);
		res+=T.ask(1,1,n,id[top[x]],id[x]);
		res%=md;
		x=f[top[x]];
	}
	if(dep[x]<dep[y])
		swap(x,y);
	res+=T.ask(1,1,n,id[y],id[x]);
	return res%md;
}
inline void cTree(int x,int z){
	T.change(1,1,n,id[x],id[x]+sz[x]-1,z);
}
inline int qTree(int x){
	return T.ask(1,1,n,id[x],id[x]+sz[x]-1)%md;
}
int main(){
	n=read();m=read();r=read();p=read();
	F(i,1,n)
		v[i]=read();
	F(i,1,n-1){
		int from=read(),to=read();
		ins(from,to);ins(to,from);
	}
	dep[r]=1;
	dfs1(r);
	top[r]=r;
	dfs2(r,r);
	T.build_tree(1,1,n);
	F(p,1,m){
		int kd=read(),x,y,z;
		if(kd==1)
			x=read(),y=read(),z=read(),cRange(x,y,z);
		if(kd==2)
			x=read(),y=read(),printf("%d\n",qRange(x,y));
		if(kd==3)
			x=read(),z=read(),cTree(x,z);
		if(kd==4)
		    printf("%d\n",qTree(read()));
	}
	return 0;
}

Ⅳ、例题

[Zjoi2008]树的统计

题目传送门
题意很简单，树上单点修改，区间查询最大值与和，树剖裸题，线段树练手题

#include<bits/stdc++.h>
#define ll long long
#define INF 2147483647
#define mem(i,j) memset(i,j,sizeof(i))
#define F(i,j,n) for(register ll i=j;i<=n;i++)
#define md p
using namespace std;
struct hahaha{
    ll from,to,nxt;
}s[200010];
ll n,m,r,p,head[200010],cnt=0,pls[1000010];
ll v[100010],f[100010],son[100010];
ll dep[100010],top[100010],sz[100010];
ll id[1000010],vt[1000010],num=0;
inline ll read(){
    ll datta=0;char chchc=getchar();bool okoko=0;
    while(chchc<'0'||chchc>'9'){if(chchc=='-')okoko=1;chchc=getchar();}
    while(chchc>='0'&&chchc<='9'){datta=datta*10+chchc-'0';chchc=getchar();}
    if(okoko==1)return -datta;
    return datta;
}
inline void ins(ll from,ll to){
    s[++cnt].from=from;
    s[cnt].to=to;
    s[cnt].nxt=head[from];
    head[from]=cnt;
}
inline ll dfs1(ll from){
    ll tmp=0,tmx=0,ti=0;
    for(ll i=head[from];i;i=s[i].nxt){
        ll to=s[i].to;
        if(to!=f[from]){
            dep[to]=dep[from]+1;
            f[to]=from;
            tmp=dfs1(to);
            sz[from]+=tmp;
            if(tmp>tmx)
                tmx=tmp,ti=to;
        }
    }
    sz[from]++;
    son[from]=ti;
    return sz[from];
}
inline void dfs2(ll from,ll tp){
    id[from]=++num,vt[num]=v[from];
    if(son[from])
        top[son[from]]=tp,dfs2(son[from],tp);
    for(ll i=head[from];i;i=s[i].nxt){
        ll to=s[i].to;
        if(to!=f[from]&&to!=son[from])
            top[to]=to,dfs2(to,to);
    }
}
struct Segment_Tree{
    #define ls u<<1
    #define rs u<<1|1
    #define mid ((l+r)>>1)
    ll tree[1000010],mx[1000010];
    void updata(ll u){
        tree[u]=tree[ls]+tree[rs];
        mx[u]=max(mx[ls],mx[rs]);
    }
    void build_tree(ll u,ll l,ll r){
        mx[u]=-2147483647;
        if(l==r){
            tree[u]=mx[u]=vt[l];
            return ;
        }
        build_tree(ls,l,mid);
        build_tree(rs,mid+1,r);
        updata(u);
    }
    void change(ll u,ll l,ll r,ll x,ll z){
        if(l==r){
            tree[u]=z;
            mx[u]=z;
            return ;
        }
        if(x<=mid)
            change(ls,l,mid,x,z);
        else
            change(rs,mid+1,r,x,z);
        updata(u);
    }
    ll askmx(ll u,ll l,ll r,ll x,ll y){
        ll res=-214748364700;
        if(x<=l&&r<=y)
            return mx[u];
        if(x<=mid)
            res=askmx(ls,l,mid,x,y);
        if(y>=mid+1)
            res=max(res,askmx(rs,mid+1,r,x,y));
        return res;
    }
    ll ask(ll u,ll l,ll r,ll x,ll y){
        ll res=0;
        if(x<=l&&r<=y)
            return tree[u];
        if(x<=mid)
            res+=ask(ls,l,mid,x,y);
        if(y>=mid+1)
            res+=ask(rs,mid+1,r,x,y);
        return res;
    }
}T;
inline ll qRangemx(ll x,ll y){
    ll res=-214748364700;
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]])
            swap(x,y);
        res=max(res,T.askmx(1,1,n,id[top[x]],id[x]));
        x=f[top[x]];
    }
    if(dep[x]<dep[y])
        swap(x,y);
    res=max(res,T.askmx(1,1,n,id[y],id[x]));
    return res;
}
inline ll qRange(ll x,ll y){
    ll res=0;
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]])
            swap(x,y);
        res+=T.ask(1,1,n,id[top[x]],id[x]);
        x=f[top[x]];
    }
    if(dep[x]<dep[y])
        swap(x,y);
    res+=T.ask(1,1,n,id[y],id[x]);
    return res;
}
int main(){
    n=read();r=1;
    F(i,1,n-1){
        ll from=read(),to=read();
        ins(from,to);ins(to,from);
    }
    F(i,1,n)
        v[i]=read();
    dep[r]=1;
    dfs1(r);
    top[r]=r;
    dfs2(r,r);
    T.build_tree(1,1,n);
    m=read();
    F(p,1,m){
        char ch=getchar();
        while(ch!='Q'&&ch!='C')
            ch=getchar();
        if(ch=='Q')
            ch=getchar();
        ll x=read(),y=read();
        if(ch=='C')
            T.change(1,1,n,id[x],y);
        if(ch=='S')
            printf("%lld\n",qRange(x,y));
        if(ch=='M')
            printf("%lld\n",qRangemx(x,y));
    }
    return 0;
}

Spoj 2798 Qtree3

传送门
单点修改，查询rt到某个结点第一个黑色点
考虑在线段树上维护数组lft，表示该区间内最靠近rt并且为黑色点的编号，转移时直接取左右儿子的max即可

#include<bits/stdc++.h>
#define ll long long
#define INF 2147483647
#define mem(i,j) memset(i,j,sizeof(i))
#define F(i,j,n) for(register int i=j;i<=n;i++)
using namespace std;
struct hahaha{
    int from,to,nxt;
}s[200010];
int n,m,r,p,head[200010],cnt=0,iid[100010];
int v[100010],f[100010],son[100010];
int dep[100010],top[100010],sz[100010],z[100010],nm[100010];
int id[100010],vt[100010],num=0;
inline int read(){
    int datta=0;char chchc=getchar();bool okoko=0;
    while(chchc<'0'||chchc>'9'){if(chchc=='-')okoko=1;chchc=getchar();}
    while(chchc>='0'&&chchc<='9'){datta=datta*10+chchc-'0';chchc=getchar();}
    if(okoko==1)return -datta;
    return datta;
}
inline void ins(int from,int to){
    s[++cnt].from=from;
    s[cnt].to=to;
    s[cnt].nxt=head[from];
    head[from]=cnt;
}
inline int dfs1(int from){
    int tmp=0,tmx=0,ti=0;
    for(int i=head[from];i;i=s[i].nxt){
        int to=s[i].to;
        if(to!=f[from]){
            dep[to]=dep[from]+1;
            f[to]=from;
            v[to]=z[i];
            nm[(i+1)/2]=to;
            tmp=dfs1(to);
            sz[from]+=tmp;
            if(tmp>tmx)
                tmx=tmp,ti=to;
        }
    }
    sz[from]++;
    son[from]=ti;
    return sz[from];
}
inline void dfs2(int from,int tp){
    id[from]=++num,iid[num]=from,vt[num]=v[from];
    if(son[from])
        top[son[from]]=tp,dfs2(son[from],tp);
    for(int i=head[from];i;i=s[i].nxt){
        int to=s[i].to;
        if(to!=f[from]&&to!=son[from])
            top[to]=to,dfs2(to,to);
    }
}
struct Segment_Tree{
    #define ls u<<1
    #define rs u<<1|1
    #define mid ((l+r)>>1)
    int tree[1000010],lft[1000010];
    void updata(int u){
        tree[u]=max(tree[ls],tree[rs]);
        lft[u]=min(lft[ls],lft[rs]);
    }
    void build_tree(int u,int l,int r){
        lft[u]=2147483647;
        if(l==r)
            return ;
        build_tree(ls,l,mid);
        build_tree(rs,mid+1,r);
    }
    void change(int u,int l,int r,int x){
        if(l==r){
            tree[u]^=1;
            lft[u]=tree[u]?l:2147483647;
            return ;
        }
        if(x<=mid)
            change(ls,l,mid,x);
        else
            change(rs,mid+1,r,x);
        updata(u);
    }
    int ask(int u,int l,int r,int x,int y){
        int res=2147483647;
        if(x<=l&&r<=y)
            return lft[u];
        if(x<=mid)
            res=ask(ls,l,mid,x,y);
        if(y>=mid+1)
            res=min(res,ask(rs,mid+1,r,x,y));
        return res;
    }
}T;
inline int qRange(int x,int y){
    int res=2147483647;
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]])
            swap(x,y);
        res=min(res,T.ask(1,1,n,id[top[x]],id[x]));
        x=f[top[x]];
    }
    if(dep[x]<dep[y])
        swap(x,y);
    res=min(res,T.ask(1,1,n,id[y],id[x]));
    return res;
}
int main(){
    n=read();m=read();r=1;
    F(i,1,n-1){
        int from=read(),to=read();
        ins(from,to);ins(to,from);
    }
    dep[r]=1;
    dfs1(r);
    top[r]=r;
    dfs2(r,r);
    T.build_tree(1,1,n);
    while(m--){
        int kd=read();
        int x=read();
        if(kd==0)
            T.change(1,1,n,id[x]);
        if(kd==1){
            int ans=qRange(r,x);
            printf("%d\n",ans==2147483647?-1:iid[ans]);
        }
    } 
    return 0;
}

[Usaco2011 Dec]Grass Planting

传送门
之前的树剖都是在结点上进行操作，这道题要求在边权上进行修改与查询
如何转化？
考虑将一条边dep较大的那个端点作为一条边的权值，即将边权转移到靠下端的结点上
具体细节看代码注释

#include<bits/stdc++.h>
#define ll long long
#define INF 2147483647
#define mem(i,j) memset(i,j,sizeof(i))
#define F(i,j,n) for(register int i=j;i<=n;i++)
using namespace std;
struct hahaha{
	int from,to,nxt;
}s[200010];
int n,m,r,p,head[200010],cnt=0;
int v[100010],f[100010],son[100010];
int dep[100010],top[100010],sz[100010],z[100010],nm[100010];
int id[1000010],vt[1000010],num=0;
inline int read(){
	int datta=0;char chchc=getchar();bool okoko=0;
	while(chchc<'0'||chchc>'9'){if(chchc=='-')okoko=1;chchc=getchar();}
	while(chchc>='0'&&chchc<='9'){datta=datta*10+chchc-'0';chchc=getchar();}
	if(okoko==1)return -datta;
	return datta;
}
inline void ins(int from,int to){
	s[++cnt].from=from;
	s[cnt].to=to;
	s[cnt].nxt=head[from];
	head[from]=cnt;
}
inline int dfs1(int from){
	int tmp=0,tmx=0,ti=0;
	for(int i=head[from];i;i=s[i].nxt){
		int to=s[i].to;
		if(to!=f[from]){
			dep[to]=dep[from]+1;
			f[to]=from;
			v[to]=z[i];
			nm[(i+1)/2]=to;
			tmp=dfs1(to);
			sz[from]+=tmp;
			if(tmp>tmx)
				tmx=tmp,ti=to;
		}
	}
	sz[from]++;
	son[from]=ti;
	return sz[from];
}
inline void dfs2(int from,int tp){
	id[from]=++num,vt[num]=v[from];
	if(son[from])
		top[son[from]]=tp,dfs2(son[from],tp);
	for(int i=head[from];i;i=s[i].nxt){
		int to=s[i].to;
		if(to!=f[from]&&to!=son[from])
			top[to]=to,dfs2(to,to);
	}
}
struct Segment_Tree{
	#define ls u<<1
	#define rs u<<1|1
	#define mid ((l+r)>>1)
	int tree[1000010];
	void updata(int u){
		tree[u]=max(tree[ls],tree[rs]);
	}
	void build_tree(int u,int l,int r){
		if(l==r){
			tree[u]=vt[l];
			return ;
		}
		build_tree(ls,l,mid);
		build_tree(rs,mid+1,r);
		updata(u);
	}
	void change(int u,int l,int r,int x,int z){
		if(l==r){
			tree[u]=z;
			return ;
		}
		if(x<=mid)
			change(ls,l,mid,x,z);
		else
			change(rs,mid+1,r,x,z);
		updata(u);
	}
	int ask(int u,int l,int r,int x,int y){
		int res=0;
		if(x<=l&&r<=y)
			return tree[u];
		if(x<=mid)
			res=ask(ls,l,mid,x,y);
		if(y>=mid+1)
			res=max(res,ask(rs,mid+1,r,x,y));
		return res;
	}
}T;
inline int qRange(int x,int y){
	int res=0;
	while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]])
			swap(x,y);
		res=max(res,T.ask(1,1,n,id[top[x]],id[x]));
		x=f[top[x]];
	}
	if(x==y)//防止多累加答案
		return res;
	if(dep[x]<dep[y])
		swap(x,y);
	res=max(res,T.ask(1,1,n,id[y]+1,id[x]));//id[y]+1即为id[son[y]]，这么写是因为id[y]+1存着y->son[y]这条边
	return res;
}
int main(){
	m=read();
	while(m--){
		mem(s,0);mem(head,0);cnt=0;mem(v,0);mem(f,0);mem(son,0);mem(dep,0);mem(top,0);mem(sz,0);
		mem(z,0);mem(nm,0);mem(id,0);mem(vt,0);num=0;mem(T.tree,0);
		n=read();r=1;
		F(i,1,n-1){
			int from=read(),to=read();
			z[i*2-1]=z[i*2]=read();
			ins(from,to);ins(to,from);
		}
		dep[r]=1;
		dfs1(r);
		top[r]=r;
		dfs2(r,r);
		T.build_tree(1,1,n);
		while(1){
			char ch=getchar();
			while(ch!='Q'&&ch!='C'&&ch!='D')
				ch=getchar();
			if(ch=='D')
				return 0;
			int x=read(),y=read();
			if(ch=='C')
				T.change(1,1,n,nm[x],y);
			if(ch=='Q')
				printf("%d\n",qRange(x,y));
		}
	}
	return 0;
}