概率论——随机变量及其分布

【随机变量】

设随机实验的样本空间是 S=|e| ，X = X(e) 是定义在样本空间S上的实值单值函数，称 X = X(e) 为随机变量。

【概率分布率】

设随机变量 X ，其所有可能去的不同值为：

取各个值的可能的概率分别为：

即：

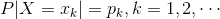
若该公式满足以下条件，则称为随机变量X的概率分布率，简称分布率。

  ，  

 

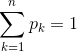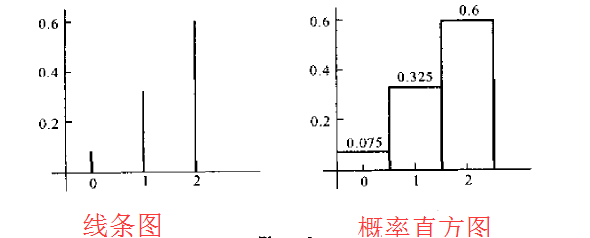
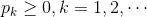
 【概率直方图】

 

概率直方图：直方图中面积之和为1.

 

【伯努利试验】

假设实验 E 只有两个可能的结果：成功与失败，则称 E 为伯努利试验。

将 E （0<p<1）独立重复进行 n 次，则称这一串重复的独立使用为 n重伯努利试验。

 

【伯努利分布、二项分布】

事件发生的概率记为 p，不发生概率为 (1-p) ，则 n 次实验中在前 k 次发生的概率为：

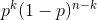
因为事件独立， n 次中发生 k 次的顺序不固定， n 次实验中发生 k 次的概率为：

 

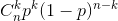
若随机变量 X 具有分布率：

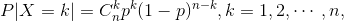
其中 0<p<1 为常数时，则称 X 服从 n,p 为参数的二项分布，记为  X ~ B(n，p)

 当 n=1 时，公式简化为：

 

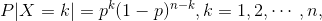
此称 X 服从以 p 为参数的 伯努利分布 或 {0 - 1} 分布。

 

【泊松分布】

 设随机变量 X 的分布率为：

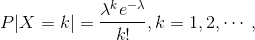
其中  “入 > 0 ” 是常数，则称随机变量 X 服从以 “入 ” 为参数的泊松分布，记为：

 

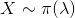
 【连续型随机变量及其概率密度】

 栗子：射击运动员射击，圆盘半径为 r，随机变量 X 为击中点到靶心的距离。

假设每次都中靶，射击结果如图：

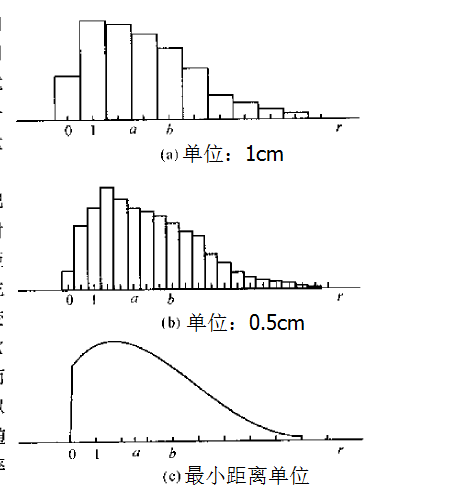
曲线面积为1，区间 [a,b] 的概率为之间的面积。存在一个函数，使得 X 落在[a,b] 区间概率为：

 

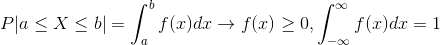
称 X 是连续型随机变量，f(x) 称为 X 的概率密度函数，简称概率密度。

 附加说明：∫  用于求曲边多边形的面积（导函数符号，求原函数），牛顿-莱布尼茨公式：

 

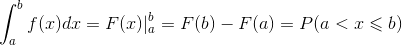
 【均匀分布】

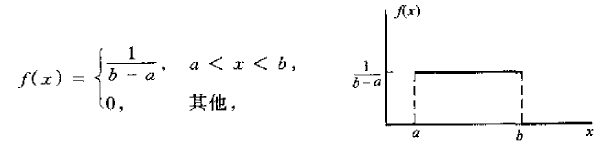
【指数分布】

 

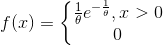
【正太分布】

 

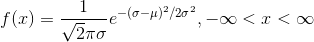
正太分布、高斯分布，正太分布满足以下条件：

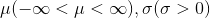
【标准正太分布】

 

 

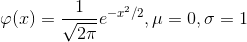
 【分布函数】

 

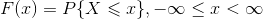
分布函数在 x 处可导，导函数为概率密度函数。

 【多维随机变量分布】