【人工智能实战2019-何峥】第3次作业

使用minibatch的方式进行梯度下降

作业要求

项目	内容
课程	人工智能实战2019
作业要求	采用随机选取数据的方式，batch size分别选择5，10，15进行运行，并回答关于损失函数的 2D 示意图的问题
我的课程目标	掌握相关知识和技能，获得项目经验
本次作业对我的帮助	理解神经网络的基本原理，并掌握代码实现的基本方法
作业正文	【人工智能实战2019-何峥】第3次作业
其他参考文献	梯度下降的三种形式 参考代码 ch04/level4-final

作业正文

1. 采用随机选取数据的方式，batch size分别选择5，10，15进行运行。画出Loss图。

Loss图

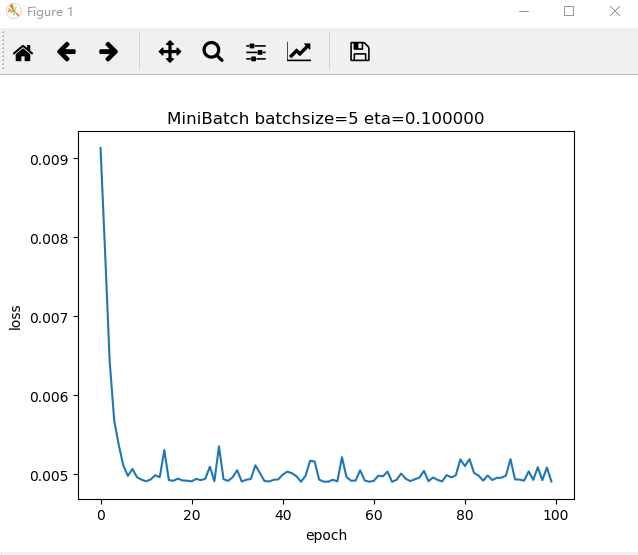
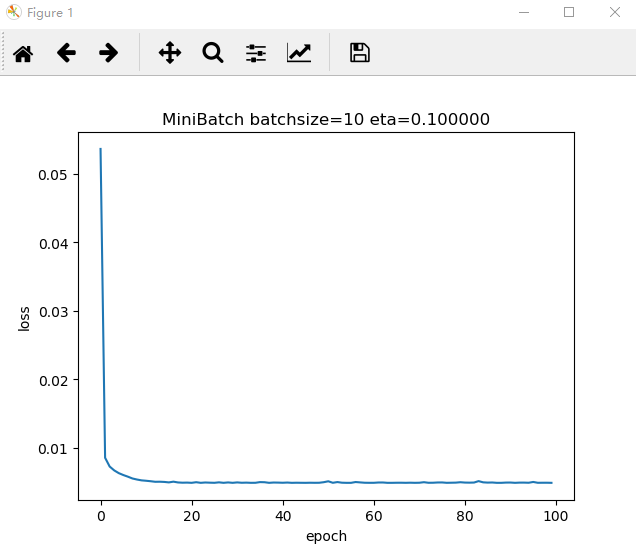
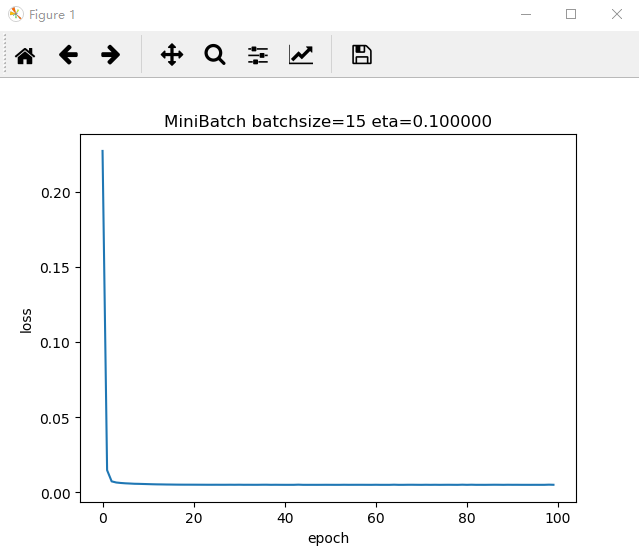
代码展示

import numpy as np
import matplotlib.pyplot as plt
from pathlib import Path
import random

x_data_name = "D:\VSCODEPROJECTS\AI_py\TemperatureControlXData.dat"
y_data_name = "D:\VSCODEPROJECTS\AI_py\TemperatureControlYData.dat"

def ReadData():
    Xfile = Path(x_data_name)
    Yfile = Path(y_data_name)
    print(Xfile)
    if Xfile.exists() & Yfile.exists():
        X = np.load(Xfile)
        Y = np.load(Yfile)
        return X.reshape(1,-1),Y.reshape(1,-1)
    else:
        return None,None

def ForwardCalculationBatch(W,batch_x,B):
    Z = np.dot(W,batch_x) + B
    return Z

def BackwardCalculationBatch(batch_x,batch_y,batch_z):
    k = batch_y.shape[1]
    dZ = batch_z-batch_y
    dW = np.dot(dZ,batch_x.T)/k
    dB = dZ.sum(axis=1,keepdims=True)/k
    return dW,dB

def UpdateWeights(dW,dB,W,B,eta):
    W = W - eta*dW
    B = B - eta*dB
    return W,B

def RandomSample(X,Y,batchsize):
    batch_x = np.zeros((1,batchsize))
    batch_y = np.zeros((1,batchsize))
    for i in range(batchsize):
        if X.shape[1]==0:
            print("wrong")
            break
        else:
            r=random.randint(0,X.shape[1]-1)
            batch_x[0,i] = X[0,r]
            X = np.delete(X,i,axis=1)
            batch_y[0,i] = Y[0,r]
            Y = np.delete(Y,i,axis=1)
    return batch_x, batch_y

def InitialWeights(n,f):
    W = np.zeros((n,f))
    B = np.zeros((n,1))
    return W,B

def GetLoss(W,B,X,Y):
    Z = np.dot(W, X) + B
    m = X.shape[1]
    Loss = (Z - Y)**2
    loss = np.sum(Loss)/m/2
    return loss

def LossList(LOSS,loss):
    LOSS.append(loss)
    return LOSS

def Loss_EpochPicture(LOSS,batchsize,eta):
    plt.plot(LOSS)
    plt.title("MiniBatch batchsize=%d eta=%f"  % (batchsize,eta) )
    plt.xlabel("epoch")
    plt.ylabel("loss")
    plt.show()

if __name__ == '__main__':
    X,Y = ReadData()
    num_example = X.shape[1]
    #initial parameters
    batchsize = 5 #10,15
    n = 1
    f = 1
    LOSS=[]
    eta = 0.1
    max_epoch = 100

    iteration =int( num_example / batchsize)
    print(iteration)
    W,B = InitialWeights(n,f)    
    for epoch in range(max_epoch):
        X1 = X
        Y1 = Y
        batch_x, batch_y = RandomSample(X1,Y1,batchsize)
        for i in range(iteration):
            batch_x,batch_y = RandomSample(X1,Y1,batchsize)
            batch_z = ForwardCalculationBatch(W,batch_x,B)
            dW,dB = BackwardCalculationBatch(batch_x,batch_y,batch_z)
            W,B = UpdateWeights(dW,dB,W,B,eta)
        loss = GetLoss (W,B,X,Y)
        LOSS = LossList (LOSS,loss)
    Loss_EpochPicture(LOSS,batchsize,eta)

2. 解释2D图的问题

• 解释为什么是椭圆而不是圆？如何把这个图变成一个圆？

\(LOSS\)=\(1/2*1/k*\) \(\sum_{i=1}^k(wx_i+b-y_i)\) = \(1/2*1/k*\) \(\sum_{i=1}^k\) \((x_i^2w^2\)+\(b^2\)+\(2x_iwb-2y_ib\)-\(2x_iy_iw\)+\(y_i^2)\)
由上述公式可以得知，当LOSS取某一定值（即在图上表现为某一特定颜色时），该式符合椭圆表达式的一般形式，因此2D的LOSS图像表现为椭圆。若想把图转换为一个圆，则需保证\(w^2\)和\(b^2\)前的系数相等同时\(wb\)前的系数为0。即当满足\(\sum_{i=1}^kx_i^2=k\)，且\(\sum_{i=1}^kx_i=0\)时，图形为圆形。

• 为什么中心是个椭圆区域而不是一个点？

由于所取的数值精度有限，并非完全连续，因此LOSS函数在趋近于最小值0时，由于平面变化趋向平缓，因此0值相近的区域都表现为同一颜色表示，即形成所见的椭圆。