史上最快平衡树——红黑树

红黑树是一种二叉搜索树，单次操作复杂度上限$logn$，效率极高，基本用指针实现。

为了减小常数，红黑树的操作全部非递归实现。

下面系统介绍一下红黑树，包括复杂度的证明和基本操作。

1、红黑树的结构：

　　红黑树是二叉搜索树，满足BST性质，左儿子数值都小于当前节点，右儿子数值都大于当前节点，中序遍历单调递增。

　　红黑树根节点的父亲和叶节点的儿子指向同一个节点，称为红黑树的叶节点。　　

　　叶节点不仅具有哨兵的作用，也可以减少情况，简化代码，哨兵可以当作普通的黑色节点。

　　叶节点以外得点被称为红黑树的内节点。

　　每个节点有六个域，分别为$key$，$si$，$we$，$co$，$f$和$ch$，$key$代表当前点的权值，$we$代表当前值的个数，$si$代表子树大小，$ch$代表左右儿子，$f$代表父亲，$co$代表当前节点的颜色。

　　设$bh(x)$为节点$x$到叶节点的一条路径上的黑色节点数目，称为该节点的黑高，红黑树的黑高为根节点的黑高。

　　设$h(x)$为节点$x$到叶节点的所有路径中最长的一条的长度。

　　设$rt$代表红黑树的根。

　　一颗完整的红黑树如下图：

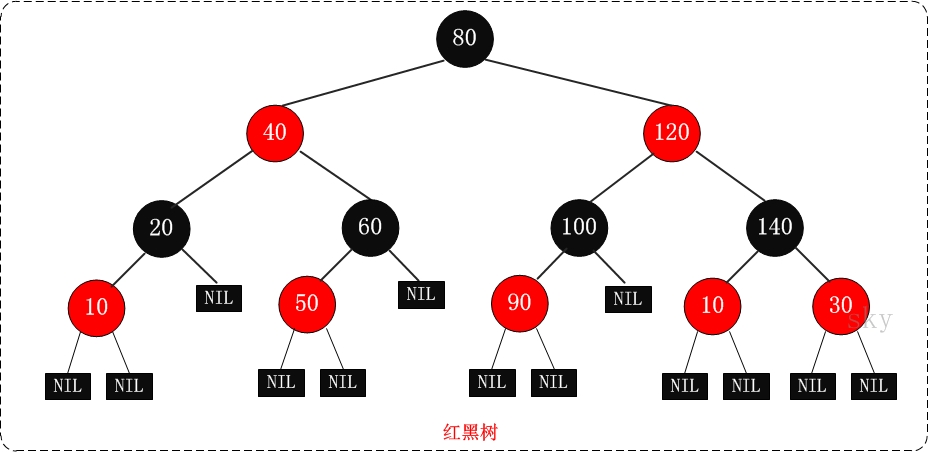
2、红黑树的性质：

　　一颗完整的红黑树具有以下性质：

　　　　1、每个节点都是红色或黑色；

　　　　2、根节点和叶节点是黑色；

　　　　3、红色节点的儿子都是黑色；

　　　　4、从根节点到叶节点的每条路径上经过的黑色节点数相同。

　　这些性质保证了红黑树的优秀复杂度。

3、红黑树复杂度的证明：

　　我们要证明红黑树的时间复杂度为$O(logn)$。

　　引理一：红黑树中没有任何一条从根节点到叶节点的路径比另一条长出一倍。

　　证明：

　　　　从每个节点到叶子的路径上的黑色节点数称为该节点的黑高度，记为$bh$。

　　　　根据性质4，根节点到叶节点的每条路径上黑色节点数相同；再根据性质3，红色节点的儿子都是黑色。

　　　　把根节点到叶节点的路径看成一个序列，把红色节点插入到黑色节点之间，则没有两个红色节点相邻。

　　　　所以一条路径上红色节点数不会超过黑色节点数，没有任何一条路径比另一条长出一倍。

　　　　证毕。

　　引理二：以$x$为根的子树中至少包含$2^{hb(x)}-1$个内节点。

　　证明：

　　　　用数学归纳法证明。

　　　　如果$hb(x)=0$，$x$一定是叶节点，结论显然成立。

　　　　对于其他节点，每个节点都有两个儿子，根据儿子的颜色，每个儿子的黑高为$hb(x)$或$hb(x)-1$，并且儿子节点的黑高都小于当前节点的黑高。

　　　　根据前一布的归纳可以得出，以儿子节点为根的子树内至少有$2^{hb(x)-1}-1$个节点。

　　　　所以最次情况下，即两个儿子的黑高都是$hb(x)-1$的情况下，当前子树大小可以去得最小值$2^{hb(x)}-1$，其余情况下均大于这个值。

　　　　证毕。

　　引理三：一颗含有$n$个节点的红黑树，高度至多为$2log(n+1)$。

　　证明：

　　　　根据性质3和性质4，从根到叶节点的其中一条简单路径上黑色节点占一半以上。

　　　　所以$hb(x)>=\frac{h(x)}{2}$，当$x$为根时，根据引理二，可以得到不等式：

　　　　　　$n>=2^{\frac{h}{2}}-1$

　　　　移项后取对数可得：

　　　　　　$h<=2lg(n+1)$

　　　　证毕。

4、旋转：

　　旋转是红黑树的必要操作。

　　红黑树的旋转和其他的带旋平衡树类似，会带旋treap，splay，AVL或SBT的大佬可以选择跳过。

　　旋转分为左旋和右旋，都是在维护BST性质下对树的结构进行的局部调整。

　　记住是局部调整，对红黑树的其他位置都没有影响。

　　定义$rotate(x,p)$表示以$x$的父亲为支点左/右旋，0代表右旋，1代表左旋。

　　一张图理解一下：

　　　　

 

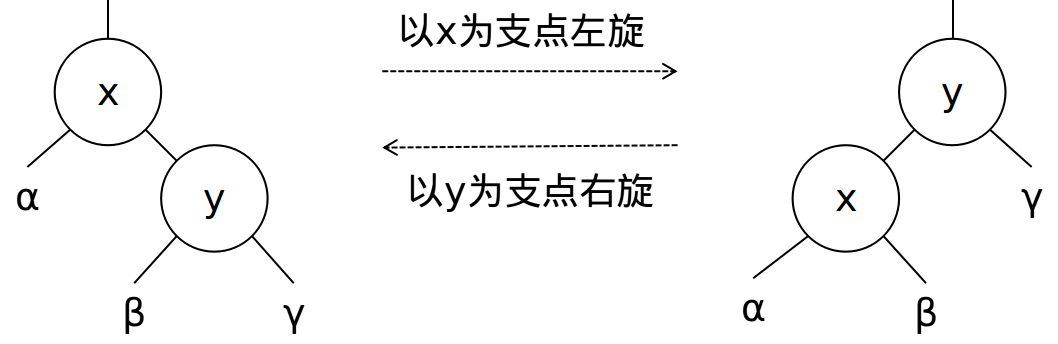
　　旋转要保证$x$和$y$均不为空（均不是哨兵），对于$\alpha$，$\beta$和$\gamma$则没有特殊要求。

　　以0代表左儿子，以1代表右儿子，就是$p^1$儿子过继给父亲，原来的祖父变为父亲，原来的父亲变为儿子。

　　左旋和右旋改变的仅有父指针和儿子指针，以及pushup时更新的子树大小，节点的其他域都没有改变。

　　经过旋转，可以调节红黑树的整体结构，使其更加平衡。

　　代码如下：

void rotate(node *now,int pos){//旋转操作
    node *c=now->ch[pos^1];
    now->ch[pos^1]=c->ch[pos];
    if(c->ch[pos]->si) c->ch[pos]->f=now;
    c->f=now->f;
    if(!now->f->si) rt=c;//旋到根
    else now->f->ch[now->f->ch[0]!=now]=c;
    c->ch[pos]=now;now->f=c;c->si=now->si;
    now->pushup();//更新子树大小
}

　　左旋和右旋的时间复杂度为$O(1)$但常数极大，制约了平衡树的效率。

　　而红黑树通过红黑染色，减少旋转的次数，使得每次旋转的次数不超过$\frac{2}{3}logn$，$n$为当前的红黑树大小，极大地优化了常数，这也是红黑树效率高的原因。

5、红黑树的查询

　　由于红黑树的插入和删除非常繁琐，我们在这里先讨论查询操作。

　　红黑树仅在插入和删除时会有结构的调整，其他情况下结构是固定的，可以和BST一样直接查询。

　　由于满足BST性质，所有查询都是从根开始。

　　1、查某个数$val$的排名：

　　　　如果当前节点权值大于$val$，查询左儿子即可；

　　　　如果当前节点权值小于$val$，把右子树大小和当前节点大小累加进答案，然后查询右儿子；

　　　　如果当前节点权值等于$val$，结束查询，答案加$1$（因为此时的答案为小于$val$的数的个数）。

　　2、查询排名为$rnk$的数：

　　　　如果当前节点左子树大小大于$rnk$，查询左儿子；

　　　　如果当前节点左子树大小和当前节点大小之和小于$rnk$，查询右儿子；

　　　　其余情况下结束查询，返回当前节点权值。

　　3、查找某一个数$val$：

　　　　如果当前节点权值大于$val$，查询左儿子；

　　　　如果当前节点权值小于$val$，查询右儿子；

　　　　如果当前节点权值等于$val$，结束查询，返回当前节点。

　　4、查询值$val$的前驱：

　　　　如果当前节点权值大于$val$，查询左儿子；

　　　　如果当前节点权值小于$val$，用当前点权值更新答案（取$max$），查询右儿子；

　　　　如果当前节点权值等于$val$，结束查询，返回答案。

　　5、查询值$val$的后继：

　　　　初始化答案为$inf$。

　　　　如果当前节点权值大于$val$，用当前点权值更新答案（取$minx$），查询左儿子；

　　　　如果当前节点权值小于$val$，查询右儿子；

　　　　如果当前节点权值等于$val$，结束查询，返回答案。

　　代码如下：

node *find(reg node *now,int key){//查找位置
    for(;now->si&&now->key!=key;now=now->ch[now->key<key]);
    return now;
}
int rnk(int key){//查排名
    reg int res,ans=0;
    for(reg node *now=rt;now->si;){
        res=now->ch[0]->si;
        if(now->key==key) break;
        else if(now->key>key) now=now->ch[0];
        else{
            ans+=res+now->we;now=now->ch[1];
        }
    }
    return ans+res+1;
}
int kth(int k){//查数
    reg int res;reg node *now=rt;
    for(;now->si;){
        res=now->ch[0]->si;
        if(k<=res) now=now->ch[0];
        else if(res+1<=k&&k<=res+now->we) break;
        else{
            k-=res+now->we;now=now->ch[1];
        }
    }
    return now->key;
}
int pre(int key){//前驱
    reg int res=0;
    for(reg node *now=rt;now->si;){
        if(now->key<key){
            res=now->key;now=now->ch[1];
        }
        else now=now->ch[0];
    }
    return res;
}
int nxt(int key){//后继
    reg int res=0;
    for(reg node *now=rt;now->si;){
        if(now->key>key){
            res=now->key;now=now->ch[0];
        }
        else now=now->ch[1];
    }
    return res;
}

6、红黑树的插入：

　　如果树中有对应权值，那么问题很简单，找到对应权值，将路径上的节点$si$加一即可。

　　但是对于其他情况如何处理。

　　插入时会影响到红黑树的整体结构，破坏红黑树的性质。

　　为了维持优秀的复杂度及常数，我们需要对插入进行修正。

　　在插入的同时维护红黑树的性质并不简单，我们可以先找到一个位置，将新节点插进去，再对树进行调整。

　　插入代码如下：

inline void insert(int key){//插入节点
    reg node *now=rt,*fa=nul;int pos;
    for(;now->si;now=now->ch[pos]){
        now->si++;fa=now;
        pos=now->getpos(key);
        if(pos==-1){//找到对应值
            now->we++;return;
        }
    }
    now=New(key);//找到位置，插入节点
    if(fa->si) fa->ch[key>fa->key]=now;
    else rt=now;
    now->f=fa;insert_transfrom(now);
}

　　然后我们就可以进行繁琐的修正过程了。

　　首先对节点有如下定义：

　　

 

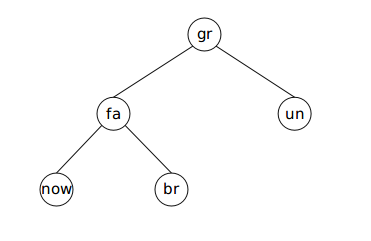
　　其中，$fa$代表父亲，$gr$代表祖父，$un$代表叔叔，$br$代表兄弟。　　

　　插入的新节点要染一个颜色，那么染什么颜色好呢。

　　由于我们并不知道树的具体形态和着色方案，所以染红色或黑色都有可能破坏树的结构和性质。

　　我们可以发现，染成黑色可能破坏性质4，染成红色可能破坏性质3和2，然而可以发现性质3的修正比较容易，所以新建节点染成红色。

　　我们需要一个迭代过程进行修正。

　　迭代的过程中要维持性质4不被破坏，并且破坏性质2和3的点不超过一个，不然我们的操作就没有意义了。

　　初始时最多有一个不满足性质的节点，也就是新插入的节点，每次修正都会修正当前节点，并产生至多一个新的不满足性质3的节点。而且这个节点的深度一定小于之前的点，所以红黑树修正的时间复杂度为$O(logn)$。

　　可以发现因为破坏性质2和3都需要该点为红色，而破坏性质3还需要父亲为红色。

　　如果破坏性质2，那么该点一定为根节点，直接染黑即可。

　　其余情况下，如果父亲为黑色，一定满足性质，迭代到达终点。而父亲是红色时，也就是需要调整时，祖父一定是黑色。

　　情况一：叔叔为红色。

　　解决方法：将父亲和祖父染黑，祖父染红，继续处理祖父。

　　不难发现，红黑树的性质3得到修正，并且性质4没有破坏。

　　如图所示：

　　　　

　　情况二：叔叔为黑色，且当前点，父亲和祖父不共线。

　　解决方法：以父亲为支点向当前点的反方向旋转，继续处理原父亲。

　　这样可以在维持性质的同时转化为情况三。

　　如图所示：

　　　　

　　最后要将根设为黑色，因为有性质2。