模拟测试64

T1：

　　根据贪心策略，在价格较小的时候买入，价格较大的时候卖出，获得的价值才会更大。

　　每天都可以和之前的一天组成匹配，贡献为差值。

　　先用一个小根堆，维护还没有匹配的权值，从前向后扫，若堆顶比当前权值小，则组成匹配，累加差值，并将当前权值插入。

　　我们发现，在同一天买入和卖出，等价于这天没有操作。

　　也就是说如果连续弹出一段权值，中间的权值实际上没有被弹出。

　　我们可以把这些权值插入第二个小根堆里，两个堆同时查询。

　　时间复杂度$O(nlogn)$

T2：

　　我们可以简单的推出$S_n^m$向四个方向的$O(1)$递推式。

　　显然：$S_n^{m+1}=S_n^m+C_n^m$，$S_n^{m-1}=S_n^m-C_n^m$。

　　然后考虑上下转移。

　　

 

 

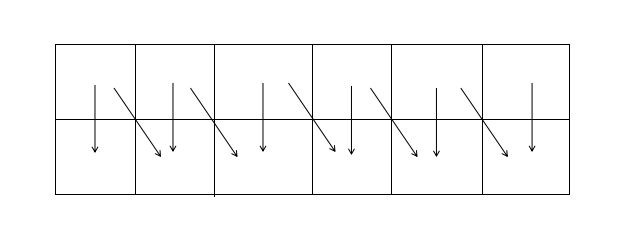
 　　可以看出，向下转移时，除了最后一行，其他组合数的贡献都是自身的2倍。

　　所以可以得出：$S_{n+1}^m=2S_n^m-C_n^m$，$S_{n-1}^m=\frac{S_n^m+C_{n-1}^m}{2}$。

　　然后莫队即可。

　　时间复杂度$O(n\sqrt{n})$。

T3：

　　大模拟。

　　我们发现，对于任何一个矩形，宽都为一，我们可以选取两端点的上下左右共6个点等效替代这个矩形。

　　对于每个矩形，查找这6个点有没有其他矩形即可。

　　先将询问离线排序，一行一行加入，用并查集维护连通性。

　　开两个vector将横条插入当前行，第一个vector储存竖条的上端点，第二个储存下端点。

　　每次将第一个vector的个数累加，并扫一遍在当前行的第一个vector里的矩形，更新上部的关键点。

　　同时扫一边上一行的第二个vector，更新下部的关键点。

　　答案既是当前矩形个数减去并查集的边数。

　　时间复杂度$O(nlogn)$。