POJ 1759

Garland

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 1236		Accepted: 547

Description

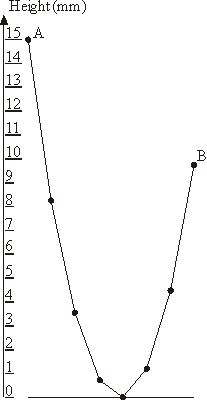The New Year garland consists of N lamps attached to a common wire that hangs down on the ends to which outermost lamps are affixed. The wire sags under the weight of lamp in a particular way: each lamp is hanging at the height that is 1 millimeter lower than the average height of the two adjacent lamps. 

The leftmost lamp in hanging at the height of A millimeters above the ground. You have to determine the lowest height B of the rightmost lamp so that no lamp in the garland lies on the ground though some of them may touch the ground. 

You shall neglect the lamp's size in this problem. By numbering the lamps with integers from 1 to N and denoting the ith lamp height in millimeters as Hi we derive the following equations: 

H1 = A 
Hi = (H_i-1 + H_i+1)/2 - 1, for all 1 < i < N 
HN = B 
Hi >= 0, for all 1 <= i <= N 

The sample garland with 8 lamps that is shown on the picture has A = 15 and B = 9.75. 

Input

The input file consists of a single line with two numbers N and A separated by a space. N (3 <= N <= 1000) is an integer representing the number of lamps in the garland, A (10 <= A <= 1000) is a real number representing the height of the leftmost lamp above the ground in millimeters.

Output

Write to the output file the single real number B accurate to two digits to the right of the decimal point representing the lowest possible height of the rightmost lamp.

Sample Input

692 532.81

Sample Output

446113.34

Source

Northeastern Europe 2000

 

二分答案，判断的时候设第二个数为0,依此递推后面n - 2个数，当第二个数加a 时，后面的数依次增加 i - 1,根据此规律可以判断。

 

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

#define maxn 1005
#define eps 1e-3

int n;
double a;
double s[maxn];

bool check(double x) {
        if(x < s[n]) return false;
        for(int i = 3; i <= n; ++i) {
                if(s[i] + (x - s[n]) / ((n - 1))  * (i - 1) < 0) return false;
        }
        return true;
}

void solve() {
        s[1] = a;
        s[2] = 0;
        double _min = 0;
        for(int i = 3; i <= n; ++i) {
                s[i] = (s[i - 1] + 1) * 2 - s[i - 2];
                _min = min(_min,s[i]);
        }

        //printf("s[n] = %f %f\n",s[n],-_min);

        double l = 0,r = s[n] + (n - 1) * (_min < 0 ? -_min : 0);
        //printf("r = %f\n",r);

        while(r - l >= eps) {

                double mid = (l + r) / 2;
                //printf("%f\n",mid);
                if(check(mid)) r = mid;
                else l = mid;
        }

        printf("%.2f\n",l);


}

int main()
{

   // freopen("sw.in","r",stdin);
    scanf("%d%lf",&n,&a);

    solve();
    return 0;
}