cf div2 238 D

D. Toy Sum

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Little Chris is very keen on his toy blocks. His teacher, however, wants Chris to solve more problems, so he decided to play a trick on Chris.

There are exactly s blocks in Chris's set, each block has a unique number from 1 to s. Chris's teacher picks a subset of blocks X and keeps it to himself. He will give them back only if Chris can pick such a non-empty subset Y from the remaining blocks, that the equality holds:

"Are you kidding me?", asks Chris.

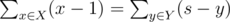
For example, consider a case where s = 8 and Chris's teacher took the blocks with numbers 1, 4 and 5. One way for Chris to choose a set is to pick the blocks with numbers 3 and 6, see figure. Then the required sums would be equal: (1 - 1) + (4 - 1) + (5 - 1) = (8 - 3) + (8 - 6) = 7.

However, now Chris has exactly s = 106 blocks. Given the set X of blocks his teacher chooses, help Chris to find the required set Y!

Input

The first line of input contains a single integer n (1 ≤ n ≤ 5·105), the number of blocks in the set X. The next line contains n distinct space-separated integers x1, x2, ..., xn (1 ≤ xi ≤ 106), the numbers of the blocks in X.

Note: since the size of the input and output could be very large, don't use slow output techniques in your language. For example, do not use input and output streams (cin, cout) in C++.

Output

In the first line of output print a single integer m (1 ≤ m ≤ 106 - n), the number of blocks in the set Y. In the next line output m distinct space-separated integers y1, y2, ..., ym (1 ≤ yi ≤ 106), such that the required equality holds. The sets X and Y should not intersect, i.e.xi ≠ yj for all i, j (1 ≤ i ≤ n; 1 ≤ j ≤ m). It is guaranteed that at least one solution always exists. If there are multiple solutions, output any of them.

Sample test(s)

input

3
1 4 5

output

2
999993 1000000

input

1
1

output

1
1000000 


如果X 集合中存在元素 i 若 s(10 ^ 6) - i + 1不在集合中则可以直接输出 s - i + 1,否则出现两个数同时出现在集合中，则可以用另外的i s - i + 1去代替

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>

using namespace std;

#define maxn 1000005

int a[maxn];
int n,s = maxn - 5;

int main() {
        //freopen("sw.in","r",stdin);
        scanf("%d",&n);

        for(int i = 1; i <= n; ++i) {
                int ch;
                scanf("%d",&ch);
                ++a[ch];
        }

        printf("%d\n",n);
        for(int i = 1; i <= maxn - 5; ++i) {
                if(a[i] > 0 && a[s - i + 1] == 0) {
                        printf("%d ",s - i + 1);
                        --n;
                }
        }
        for(int i = 1; i <= s && n; ++i) {
                if(a[i] == 0 && a[s - i + 1] == 0) {
                        printf("%d %d ",i,s - i + 1);
                        n -= 2;
                }
        }

        return 0;

}