POJ 2976

Dropping tests

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 5459		Accepted: 1889

Description

In a certain course, you take n tests. If you get a_i out of b_i questions correct on test i, your cumulative average is defined to be

.

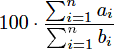Given your test scores and a positive integer k, determine how high you can make your cumulative average if you are allowed to drop any k of your test scores.

Suppose you take 3 tests with scores of 5/5, 0/1, and 2/6. Without dropping any tests, your cumulative average is 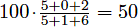. However, if you drop the third test, your cumulative average becomes .

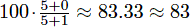Input

The input test file will contain multiple test cases, each containing exactly three lines. The first line contains two integers, 1 ≤ n ≤ 1000 and 0 ≤ k < n. The second line contains n integers indicating a_i for all i. The third line contains n positive integers indicating b_i for all i. It is guaranteed that 0 ≤ a_i ≤ b_i ≤ 1, 000, 000, 000. The end-of-file is marked by a test case with n = k = 0 and should not be processed.

Output

For each test case, write a single line with the highest cumulative average possible after dropping k of the given test scores. The average should be rounded to the nearest integer.

Sample Input

3 1
5 0 2
5 1 6
4 2
1 2 7 9
5 6 7 9
0 0

Sample Output

83
100

Hint

To avoid ambiguities due to rounding errors, the judge tests have been constructed so that all answers are at least 0.001 away from a decision boundary (i.e., you can assume that the average is never 83.4997).

Source

Stanford Local 2005

 

二分平均值。

 

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>

using namespace std;

#define maxn 1005
#define eps 1e-6

int n,k;
int a[maxn],b[maxn];

bool judge(double x) {
        double sum = 0;
        double f[maxn];
        for(int i = 1; i <= n; ++i) {
                f[i] = a[i] - x * b[i];
        }

        sort(f + 1,f + n + 1);

        for(int i = n; i >= n - (n - k) + 1; --i) {
                sum += f[i];
        }

        return sum >= 0;

}

void solve() {
        double l = 0,r = 0;

        for(int i = 1; i <= n; ++i) {
                r += a[i];
        }

        while(r - l >= eps) {
                double mid = (l + r) / 2;
                if(judge(mid)) l = mid;
                else r = mid;

        }

       // printf(" l = %f\n",l);

        printf("%d\n",(int)(100 * r + 0.5));
}

int main() {
       、、 freopen("sw.in","r",stdin);

        while(~scanf("%d%d",&n,&k)) {
        if(!n && !k) break;
        for(int i = 1; i <= n; ++i) {
                scanf("%d",&a[i]);
        }

        for(int i = 1; i <= n; ++i) {
                scanf("%d",&b[i]);
        }

        solve();

        }

        return 0;
}