决策树模型(2)特征选择

特征选择

特征选择问题

特征选择顾名思义就是对特征进行选择性截取，剔除掉冗余特征。这样能够减少决策树的复杂度。

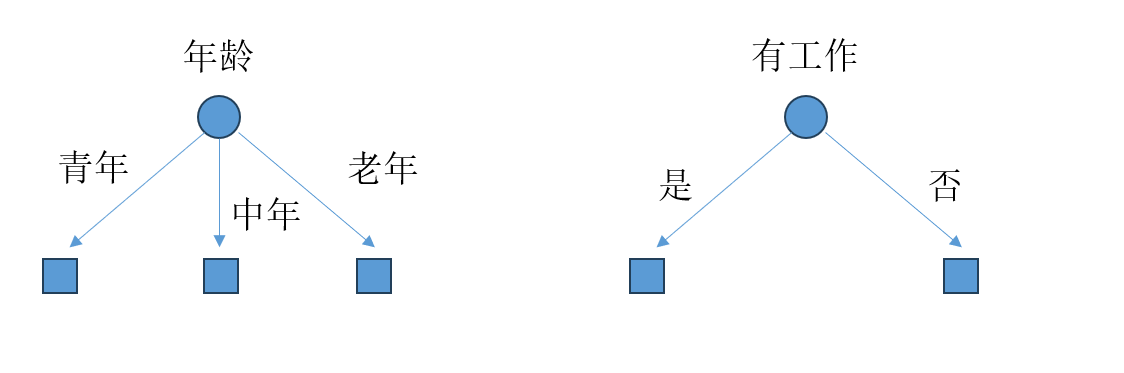
比如在上面两图中，左图通过年龄来对样本进行分类，而右图通过工作对特征进行分类，二者究竟孰好孰坏，这是需要进行比较的。一个非常直接的想法就是仅用选择的特征去训练模型，然后得出用各个特征的准确率。但是显然这样做过于繁琐与复杂，通常特征选择的准则是信息增益或信息增益比。

信息增益与信息增益比

信息增益描述了在得知已知信息(特征X)的情况下能够使得类别Y的信息的不确定性减少的程度。比如说，在不知道任何样本的特征信息情况下，我们知道Y的不确定性程度为0.7，现在你知道了样本的某个特征\(x_i\)，那么假设Y的不确定性程度减少为0.5，那么所得的信息增益即为0.2，这表示特征x对减少Y的不确定性程度的贡献。
在上面的例子中，我们提到了重要的两点，第一个是Y的不确定性程度，第二个是Y在X为某个特征时的不确定性程度。那么该怎么计算它们？

熵

熵是反应随机变量不确定性的度量。假设随机变量\(X\)的概率分布为

\[P(X=x_i)=p_i, i = 1,2,\cdots,n \]

那么其熵的定义为

\[H(X)=H(P) = -\sum_{i=1}^n p_i \mathrm{log}p_i \]

那么当随机变量\(X\)只能取0, 1时，其熵为

\[H(P) = -p\mathrm{log}p-(1-p)\mathrm{log}(1-p) \]

显然当\(p\)为0时或1时熵恰好为0，此时表明熵最小，说明随机变量\(X\)很稳定，若\(p\)为0.5，则熵对应最大，表明随机变量\(X\)很不确定，因为它取0或取1的概率相等，具有很大的不确定性。

条件熵

条件熵表示在已知随机变量\(X\)的条件下随机变量\(Y\)的不确定性。它通过下式定义

\[H(Y|X) = \sum_{i=1}^np_iH(Y|X=x_i) \]

其中\(p_i=P(X=x_i)\)

信息增益与信息增益比

信息增益表示特征\(X\)给定的情况下对\(Y\)的不确定性减少的程度，因此需要知道原本\(Y\)的熵和给定\(X\)后的熵，由下式给出

\[g(Y,X)=g(D,A)=H(D)-H(D|A) \]

其中

\[H(D)=-\sum_{k=1}^K\frac{|C_k|}{|D|}\mathrm{log}\frac{C_k}{D} \]

\[H(D|A)=\sum_{i=1}^n\frac{|D_i|}{|D|}H(D_i|A=a_i)=-\sum_{i=1}^n\frac{|D_i|}{|D|}\sum_{k=1}^K\frac{|D_{ik}|}{|D_i|}\mathrm{log}\frac{|D_{ik}|}{|D_i|} \]

其中\(D\)表示训练数据集，\(A\)表示所选特征。
通过上面的公式我们就可以计算出每个特征的信息增益啦，也就可以其进行排序，优先选择大的。
但选择信息增益存在一个问题，即倾向于选择特征取值较多的特征。比如说若编号为其特征之一，显然来说它并没有任何实际意义，但是若计算其条件熵，我们会发现对于大多数的\(H(D_i)\)其值为0，那么最后得到的条件熵也就偏低，那么最后的信息增益显然是偏大的，因此有必进行改进，一种做法是使用信息增益比

\[g_R(D,A) = \frac{g(D,A)}{H_A(D)} \]

其中\(H_A(D)\)为

\[-\sum_{i=0}^n\frac{|D_i|}{|D|}\mathrm{log}\frac{|D_i|}{|D|} \]

可以将\(H_A(D)\)视为一种罚项，当特征较多时，惩罚也大，特征少时，惩罚也小一些。