K近邻模型

k近邻模型

基本思想

\(k\)近邻算法还是很直观的，准确的来说它不是一种学习算法，而是一种统计方法，不具备学习过程，一次性就可以给出结果。
其本质思想是将特征空间划分成一个个的单元(\(cell\))，其中每个\(cell\)的区域由距离该点比其他点更近的所有点定义，所有的\(cell\)组成了整特征空间。

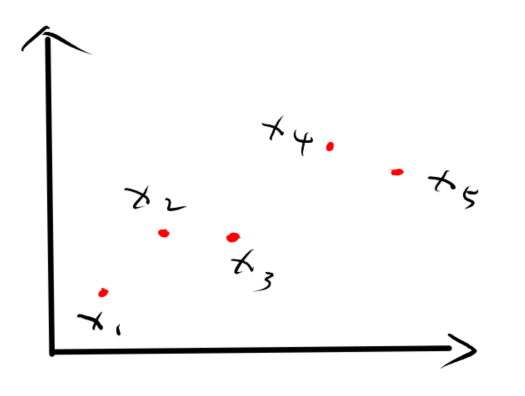
如上图所示：
考虑样本\(x_1\)构成的\(cell\)，记作\(cell_{x_1}\)

• 对于\(x_2\)，其距离\(x_3\)比\(x_1\)近，因此，\(x_2\)无法成为\(cell_{x_1}\)中的一员
• 对于\(x_3\)，其距离\(x_2\)比\(x_1\)近，因此，\(x_3\)无法成为\(cell_{x_1}\)中的一员
• 对于\(x_4\)，其距离\(x_2, x_3, x_5\)均比\(x_1\)近，因此，\(x_4\)无法成为\(cell_{x_1}\)的一员
• 对于\(x_5\)，其距离\(x_2, x_3, x_4\)均比\(x_1\)近，因此，\(x_5\)无法成为\(cell_{x_1}\)的一员
  因此，\(x_1\)组成的\(cell\)为空，即\(cell_{x_1}=\emptyset\)

再考虑样本\(x_2\)构成的\(cell\)，记作\(cell_{x_2}\)

• 对于\(x_1\)，由于没有任何一样比\(x_2\)距离\(x_1\)更近，因此\(x_1\)成为其一员
• 对于\(x_3\)，由于没有任何一样比\(x_3\)距离\(x_1\)更近，因此\(x_3\)成为其一员
• 对于\(x_4\)，其距离\(x_3, x_5\)均比\(x_2\)近，因此，\(x_4\)无法成为其一员
• 对于\(x_5\)，其距离\(x_3, x_4\)均比\(x_2\)近，因此，\(x_5\)无法成为其一员
  因此，\(cell_{x_2}=\{x_1, x_3 \}\)

同理我们可以得到\(cell_{x_3} = \{x_2\}\)，\(cell_{x_4} = \{x_5\}\)，\(cell_{x_5} = \{x_4\}\)
这样一来，有所有\(cell\)定义的区域就组成了整个空间，就可以通过每个\(cell\)构成的区域中的样本来对新样本进行预测。

上面只是理想中的方式，是一种辅助理解的办法，存在诸多问题，比如区域不好定义，上面的示例中我们只是规定了一个\(cell\)所必须包含的元素，并没有定义由这些元素构成的区域。
在实际中，我们往往直接使用与每个样本\(x\)最近的\(k\)个样本\(N_k(x)\)的类别对\(x\)的类别进行预测，比如下面的所属表决规则。
\begin{equation}
y = \mathop{\arg\max}\limits_{c_j} \sum_{x_i \in N_k{x}} I(y_i=c_j), i=1,2,\cdots,N;j=1,2,\cdots,K
\end{equation}
其中\(N\)为全体样本，\(K\)为所有类别数，而距离度量往往使用L1范数，当然其他距离也行，下面是三种常见的距离。
曼哈顿距离(L1范数)：
\begin{equation}
L_1(x_i,x_j) = \sum_{l = 1}^{n}\vert x_i^{(l)} - x_j^{(l)}\vert
\end{equation}

\[\begin{equation} L_2(x_i,x_j) = (\sum_{l = 1}^{n}\vert x_i^{(l)} - x_j^{(l)}\vert ^2)^{\frac{1}{2}} \end{equation} \]

\[\begin{equation} L_\infty(x_i,x_j) = \mathop{\max}\limits_l\vert x_i^{(l)} - x_j^{(l)}\vert \end{equation} \]

三种距离在二维空间中的等距图如下：

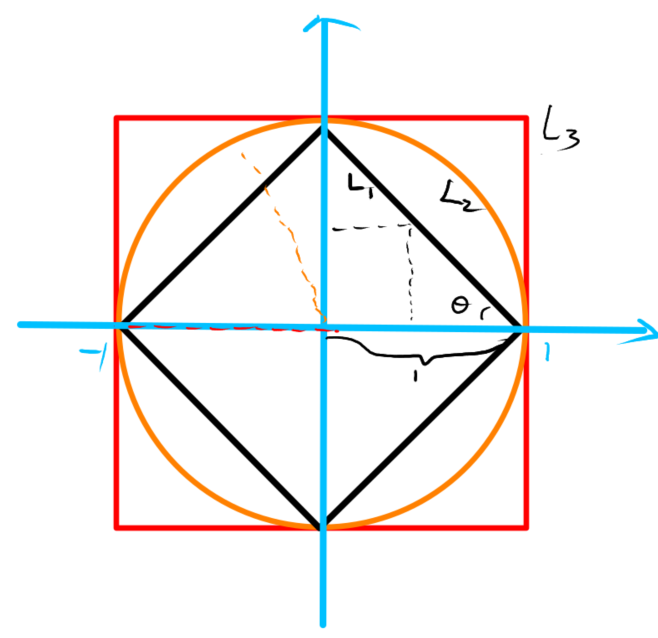
对于\(L_1\)(黑色)，由于夹角\(\theta=\frac{\pi}{4}\)，所以黑线上的点到原点的\(L1\)始终相等，由于橙色为半径为1的圆，因此橙色上的点到原点的\(L_2\)均为半径，红色为边长为2的正方形，其上的点到原点的\(L_\infty\)均为边长的一半。(图中指示错误\(L_3\)应改为\(L_\infty\))

kd树

从上面的介绍可知，若想找去每个样本的\(k\)个近邻\(N_{x_k}\)则需要计算\(N\)次后再排序选出，那么所有样本计算的时间复杂度至少是\(N^2\)级别，显然代价无法承受，因此需要一种能够有效减少冗余计算的方式。而\(kd\)树就是其中一种，它包括建树和查找两个过程。

平衡树的建立

\(kd\)树的建立过程比较简单，主要遵从如下思想：
假设样本为\(d\)维，首先取所有样本在\(d=1\)维度上的值并排序，找到中位数(若为偶数则计算二者均值)，取出中位数对应的样本(若不存在则在其相邻处随机取一个)建立根结点，并对左右两部分样本进行递归进行上述操作\(d = (d + 1) \% d\)

示例：
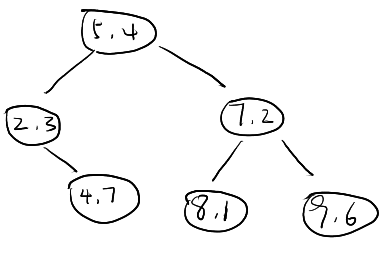
有以下二维空间中的数据集，要求建立一个\(kd\)树

\[T = \{(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)\} \]

首先让所有样本在\(d = 1\)维上进行从小到大的排序得到：

\[T_1 = \{(2,3), (4,7), (5,4), (7,2), (8,1), (9,6)\} \]

得到中位数\(=\frac{5 + 7}{2}=6\)，但是样本中不含这个样本，因此需要在两侧附件随机取1个构建根结点，机器学习课本中选择7，这里我们以5作为示例。
因此得到\(root_{T_{1}}=(5,4)\), \(T_{11}=\{(2,3), (4,7)\}\), \(T_{12}=\{(7,2), (8,1), (9,6)\}\)

继续构建下一层\(d=2\)维上样本
对于\(T_{11}\)在\(d=2\)上进行排序得到\(T_{211}=T_{11}\)，计算中位数\(=\frac{3+7}{2}=5\)，由于\(T_{211}\)中不存在第二维为5的样本，因此随机选1，这里选\(root_{T_{211}}=(2,3)\)，因此\(T_{2112}=\{(4,7)\}\)成为它的右子树(同时也是右根，右叶结点)，并且无左子树。

对于\(T_{12}\)在\(d=2\)上进行排序得到\(T_{212}=\{(8,1),(7,2),(9,6)\}\)，计算中位数\(=2\)，因此得到\(root_{T_{212}}=(7,2)\), 左子树(左根，左叶)\(T_{2121}=\{(8,1)\}\)，右子树(右根，右叶)\(T_{2122}=\{(9,6)\}\)。
至此，原始样本的对应的平衡\(kd\)树构建完毕。
下面是图例：

树的查找

树的查找包括正向和反向两个过程，正向和建树类似只需一一判断即可，反向也是必须的，因为正向过程不能保证所查找到的一定是其最近邻(需要参见\(kd\)树原始论文)。

• 正向递归查找。当给出一个样本在查找与它的最近邻样本时(限定\(L_2\)距离)时，需要依次从根节点往下查找，和建树过程类似，比如在建立第一层时用的是\(d=1\)即第一维值的大小，那么查找时也应使用样本的第一维与其第一维进行比较，该过程递归进行直至找到叶子结点。
• 反向回溯查找。在得到正向查找中与样本点\(x_i\)的近似最近邻点\(x_j\)时，以\(x_i\)为圆心，\(x_i\)到\(x_j\)的\(L_2\)距离为半径构建一个圆。回溯，依次各个区域是否与圆相交，若相交找到与其相交的最小区域对应的结点，
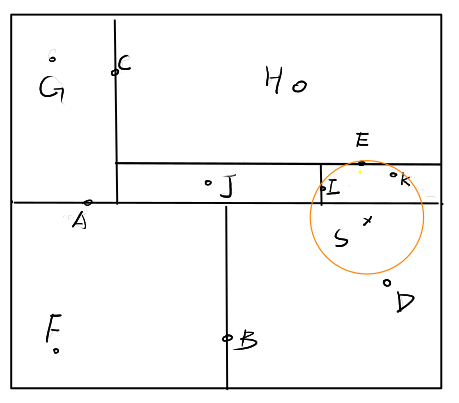
  示例：
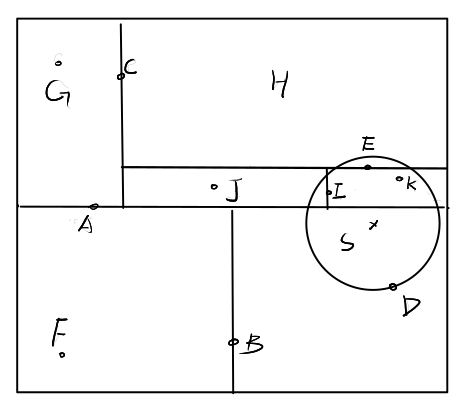
  我们考虑比机器学习课本更复杂一些的情况，如下。
  
  首先我们容易根据正向查到找到样本点\(S\)所处的区域即B的右子树对应的区域，也是叶结点\(D\)的范围。构建以\(S\)为圆心，\(d_{SD}\)为半径的圆。然后检查\(F\)对应的区域是否与圆相交，显然不相交，于是F向上回溯至A的上半部分\(C\)对应的区域，显然与圆相交。于是检查C的左区域\(G\)对应的区域，无相交，检查\(C\)的右区域\(E\)是否相交，相交，更新半径为\(d_{SE}\)，并构建新圆，如下。
  

继续检查\(E\)的上区域\(H\)是否相交,相交，但是距离太远不用更新，继续检查E的下区域\(I\)是否相交，明显相交，且半径可以更新为\(d_{IS}\)，继续这样操作之后，还可以更新半径为\(d_{KS}\)(图没画好)，最终的得到S的最近邻点\(K\)。