赫夫曼树

一、基本介绍

　　1、给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度(wpl)达到最小，称这　　样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree), 还有的书翻译为霍夫曼树。

　　2、赫夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

二、重要概念

　　1、路径和路径长度：在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1
　　2、结点的权及带权路径长度：若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积
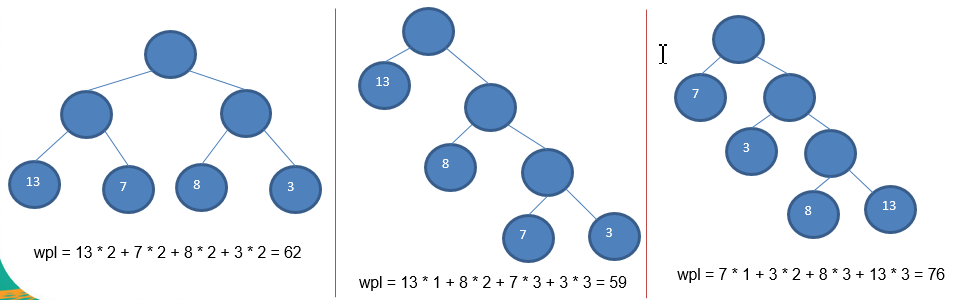
　　3、树的带权路径长度：树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL(weighted path length) ,权值越大的结点离根结点越近的二叉树才是最优二叉树。
　　4、WPL最小的就是赫夫曼树
　　

三、代码

　　

public class HuffmanTree {

    public static void main(String[] args) {
        int arr[] = { 13, 7, 8, 3, 29, 6, 1 };
        Node root = createHuffmanTree(arr);

        preOrder(root);
    }
    public static  void preOrder(Node root){
        if(root!=null){
            root.preOrder();
        }else {
            System.out.println("空数");
        }
    }

    // 创建赫夫曼树的方法
    /**
     * @param arr 需要创建成哈夫曼树的数组
     * @return 创建好后的赫夫曼树的root结点
     */
    public static Node createHuffmanTree(int[] arr){
        // 第一步为了操作方便
        // 1. 遍历 arr 数组
        // 2. 将arr的每个元素构成成一个Node
        // 3. 将Node 放入到ArrayList中
       ArrayList<Node> nodes = new ArrayList<>(arr.length);
        for (int v : arr) {
            nodes.add(new Node(v));
        }
        //我们处理的过程是一个循环的过程
        while (nodes.size()>1){
            //排序 从小到大
            Collections.sort(nodes);
            System.out.println(nodes);
            //取出根节点权值最小的两颗二叉树
            //(1) 取出权值最小的结点（二叉树）
            Node l = nodes.get(0);
            //(2) 取出权值第二小的结点（二叉树）
            Node r = nodes.get(1);
            //(3)构建一颗新的二叉树
            Node parent = new Node(l.value + r.value);
            parent.left = l;
            parent.right = r;
            //(4)从ArrayList删除处理过的二叉树
            nodes.remove(l);
            nodes.remove(r);
            //(5)将parent加入到nodes
            nodes.add(parent);
        }
        //返回哈夫曼树的root结点
        return nodes.get(0);
    }
}
// 创建结点类
// 为了让Node 对象持续排序Collections集合排序
// 让Node 实现Comparable接口
class Node implements Comparable<Node>{
    int value;// 结点权值
    char c;
    Node left;
    Node right;
    //写一个前序遍历
    public void preOrder(){
        System.out.println(this);
        if(this.left!=null){
            this.left.preOrder();
        }
        if(this.right!=null){
            this.right.preOrder();
        }
    }
    @Override
    public String toString() {
        return "Node{" +
                "value=" + value +
                '}';
    }

    public Node(int value) {
        this.value = value;
    }

    @Override
    public int compareTo(Node o) {
        return 0;
    }
}