两排序数组的中位数 Median of Two Sorted Arrays

2018-11-18 23:33:28

问题描述：

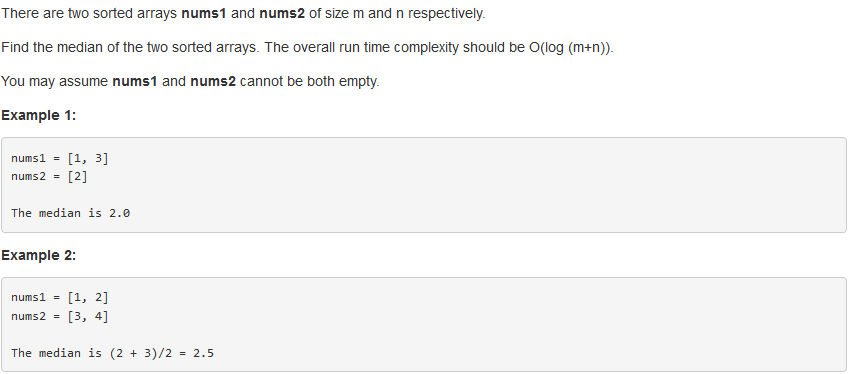
问题求解：

这个问题是一个比较有难度的可以使用二分搜索法求解的问题，如果采用朴素的解法进行merge再找中位数的话，其时间复杂度为O(n1 + n2)。但是如果使用二分查找法的话，可以将时间复杂度降到O(min(n1, n2))。

其实本题可以看成两排序数组前k小的数的特殊情况，当然了解法上是差不多的。

具体来说，我们需要找到的就是nums1对最后的前k个数到底贡献了多少个数，如果这个量确定了，那么所有的问题就迎刃而解。

所以主要的二分搜索就是在找到底nums1贡献了多少个数字，最后需要对得到的数字进行一些判断，因为nums1可能没有贡献，也可能贡献了所有的数字，这些都是需要考虑到的。

    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int n1 = nums1.length;
        int n2 = nums2.length;
        if (n1 > n2) return findMedianSortedArrays(nums2, nums1);
        // 一共需要从nums1 和 nums2 中取出k个数
        // 对于合并的数组
        // if odd : median = nums[k - 1]
        // if even : median = (nums[k - 1] + nums[k]) / 2
        int k = (n1 + n2 + 1) / 2;
        
        // 使用二分查找来判断需要从nums1中取出多少个数
        int l = 0;
        int r = nums1.length;
        while (l < r) {
            int k1 = l + (r - l) / 2;
            int k2 = k - k1;
            if (nums1[k1] < nums2[k2 - 1]) l = k1 + 1;
            else r = k1;
        }
        
        int k1 = l;
        int k2 = k - k1;
        int c1 = Math.max(k1 == 0 ? Integer.MIN_VALUE : nums1[k1 - 1], k2 == 0 ? Integer.MIN_VALUE : nums2[k2 - 1]);
        if ((n1 + n2) % 2 != 0) return c1;
        int c2 = Math.min(k1 == n1 ? Integer.MAX_VALUE : nums1[k1], k2 == n2 ? Integer.MAX_VALUE : nums2[k2]);
        return (c1 + c2) * 0.5;
    }