主元素问题 Majority Element

2018-09-23 13:25:40

主元素问题是一个非常经典的问题，一般来说，主元素问题指的是数组中元素个数大于一半的数字，显然这个问题可以通过遍历计数解决，时间复杂度为O(n)，空间复杂度为O(n)。这样的算法有两个弊端，一是空间复杂度较高，二是没法处理数据流问题。

因此就有了Boyer-Moore Majority Vote algorithm，这个算法可以用来高效的解决主元素问题，并且空间复杂度降到了O(1)，时间复杂度保持不变。

算法的思路就是将不同的元素进行抵消，最后剩余的就是最终的结果。

如果说题目中没有明确说明一定存在主元素，那么还需要额外一次遍历来确认当前的解为主元素。

一、主元素问题

问题描述：

问题求解：

    public int majorityElement(int[] nums) {
        int candidate = 0;
        int count = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] == candidate) count++;
            else if (count == 0) {
                candidate = nums[i];
                count = 1;
            }
            else count--;
        }
        return candidate;
    }

 

二、Follow Up

问题描述：

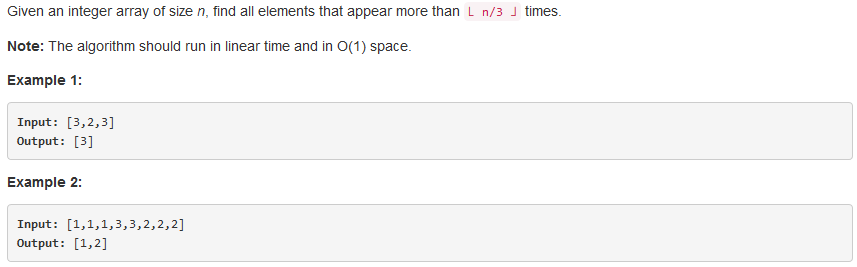
问题求解：

    public List<Integer> majorityElement(int[] nums) {
        if (nums == null || nums.length == 0) return new ArrayList<>();
        int candidate1 = 0;
        int candidate2 = 0;
        int count1 = 0;
        int count2 = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] == candidate1) count1++;
            else if (nums[i] == candidate2) count2++;
            else if (count1 == 0) {
                candidate1 = nums[i];
                count1 = 1;
            }
            else if (count2 == 0) {
                candidate2 = nums[i];
                count2 = 1;
            }
            else {
                count1--;
                count2--;
            }
        }
        List<Integer> res = new ArrayList<>();
        count1 = 0;
        count2 = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] == candidate1) count1++;
            else if (nums[i] == candidate2) count2++;
        }
        if (count1 > nums.length / 3) res.add(candidate1);
        if (count2 > nums.length / 3) res.add(candidate2);
        return res;
    }