动态规划-Stock Problem

2018-04-19 19:28:21

股票问题是leetcode里一条非常经典的题目，因为其具有一定的现实意义，所以还是在数学建模方面还是有很多用武之地的。这里会对stock的给出一个比较通用的解法，然后会针对各个细分问题用通解去解决，主要采用的算法是动态规划算法。

问题描述：Given an array representing the price of stock on each day, what determines the maximum profit we can obtain?

问题求解：首先很容易想到的是最大收入和具体结算时间以及这些天里的最多交易笔数有关，因此我们可以定义一个数组T[i][k]，表示在第i天结束时，最多经过k笔交易所产生的最大收入。很显然的，我们可以得到一个初始条件T[-1][k] = T[i][0] = 0，也就是说在第-1天，无论经过多少笔交易都没有收益，在第i天，如果最多为0次交易，那么也将不会产生收益。根据动态规划的一般思路，我们现在需要做的就是建立T[i][k]和T[i-1][k], T[i][k-1], T[i-1][k-1], ...之间的关系下面将介绍如何建立这种关系。

对于第i天的交易，我们可以采取的策略有sell，buy，rest。我们当然在最初的时候并不知道哪个选择是最优的，所以我们需要去判断一下哪个选择对于我们来说能得到一个好的结果。由于有每次只能手持一股的限制，所以我们无法在已经买过股票的情况下再购买股票，同时也无法在已经卖空股票的情况下再继续卖股票，因此，我们需要一个变量来揭示第i天结束时，手里剩余的股票数量。

因此T[i][k]的定义需要被拆分成两个：T[i][k][0] and T[i][k][1]。并且我们还可以得到如下的初始条件和递推关系：

Base cases:
T[-1][k][0] = 0, T[-1][k][1] = -Infinity
T[i][0][0] = 0, T[i][0][1] = -Infinity
Recurrence relations:
T[i][k][0] = max(T[i-1][k][0], T[i-1][k][1] + prices[i])
T[i][k][1] = max(T[i-1][k][1], T[i-1][k-1][0] - prices[i])

注意：定义一次交易为买入的时候就算作一笔交易，不可等到卖出才算作交易。

121. Best Time to Buy and Sell Stock

问题描述：

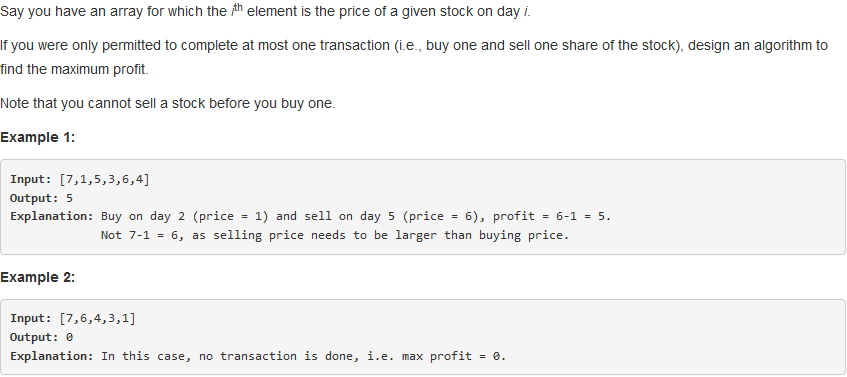
问题求解：

k = 1，则递推式变为：

T[i][1][0] = max(T[i - 1][1][0]，T[i - 1][1][1] + prices[i])

T[i][1][1] = max(T[i - 1][1][1]，0 - prices[i])

对空间复杂度进行优化，可以在<O(n)，O(1)>完成求解。

    public int maxProfit(int[] prices) {
        int Ti10 = 0;
        int Ti11 = Integer.MIN_VALUE;
        for (int price : prices) {
            Ti10 = Math.max(Ti10, Ti11 + price);
            Ti11 = Math.max(Ti11, -price);
        }
        return Math.max(Ti10, Ti11);
    }

122. Best Time to Buy and Sell Stock II

问题描述：

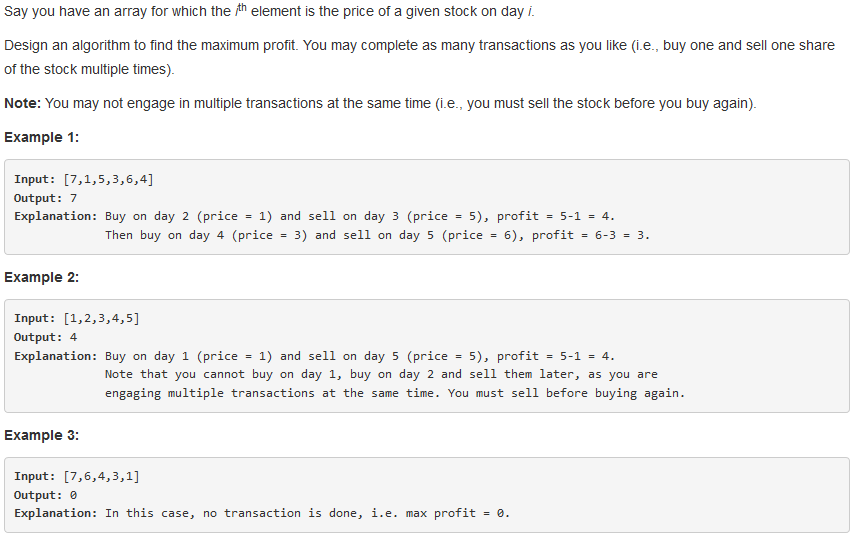
问题求解：

k = INF，则递推式变为：

T[i][k][0] = max(T[i - 1][k][0]，T[i - 1][k][1] + prices[i])

T[i][k][1] = max(T[i - 1][k][1]，T[i - 1][k][0] - prices[i])

对空间复杂度进行优化，可以在<O(n)，O(1)>完成求解。

    public int maxProfit(int[] prices) {
        int Tik0 = 0;
        int Tik1 = Integer.MIN_VALUE;
        for (int price : prices) {
            int tmp = Tik0;
            Tik0 = Math.max(Tik0, Tik1 + price);
            Tik1 = Math.max(Tik1, tmp - price);
        }
        return Math.max(Tik0, Tik1);
    }

714. Best Time to Buy and Sell Stock with Transaction Fee

问题描述：

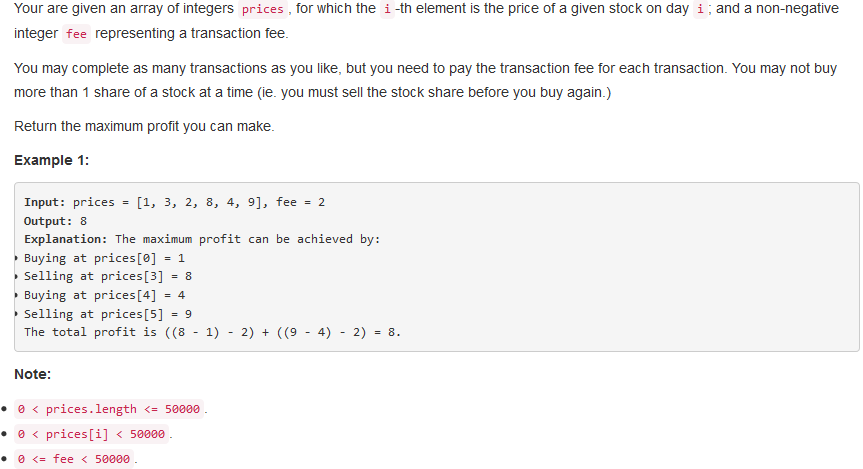
问题求解：

k = INF with fee，则递推式变为：

T[i][k][0] = max(T[i - 1][k][0]，T[i - 1][k][1] + prices[i])

T[i][k][1] = max(T[i - 1][k][1]，T[i - 1][k][0] - prices[i] - fee)

对空间复杂度进行优化，可以在<O(n)，O(1)>完成求解。

    public int maxProfit(int[] prices, int fee) {
        int Tik0 = 0;
        int Tik1 = Integer.MIN_VALUE;
        for (int i = 0; i < prices.length; i++) {
            int tmp = Tik0;
            Tik0 = Math.max(Tik0, Tik1 + prices[i]);
            Tik1 = Math.max(Tik1, tmp - prices[i] - fee);
        }
        return Tik0;
    }

309. Best Time to Buy and Sell Stock with Cooldown

问题描述：

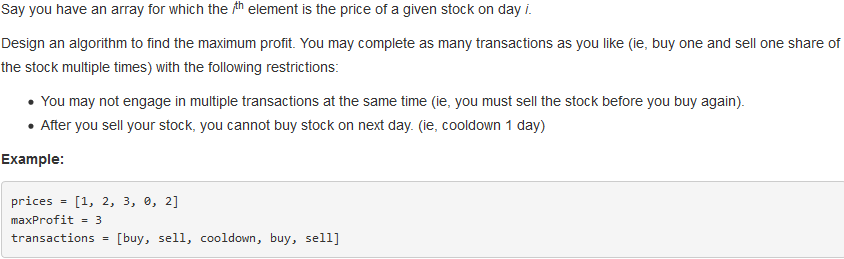
问题求解：

k = INF with cooldown，则递推式变为：

T[i][k][0] = max(T[i - 1][k][0]，T[i - 1][k][1] + prices[i])

T[i][k][1] = max(T[i - 1][k][1]，T[i - 2][k][0] - prices[i] )

对空间复杂度进行优化，可以在<O(n)，O(1)>完成求解。

    public int maxProfit(int[] prices) {
        int Tik0 = 0;
        int Tik1 = Integer.MIN_VALUE;
        int prev = 0;
        for (int price : prices) {
            int tmp = Tik0;
            Tik0 = Math.max(Tik0, Tik1 + price);
            Tik1 = Math.max(Tik1, prev - price);  // T[i - 1][k][0] 若是 rest，则T[i - 1][k][0] = T[i - 2][k][0]，若卖出，则对于第 i 天 buy 只能选择T[i - 2][k][0]
            prev = tmp;
        }
        return Math.max(Tik0, Tik1);
    }

123. Best Time to Buy and Sell Stock III

问题描述：

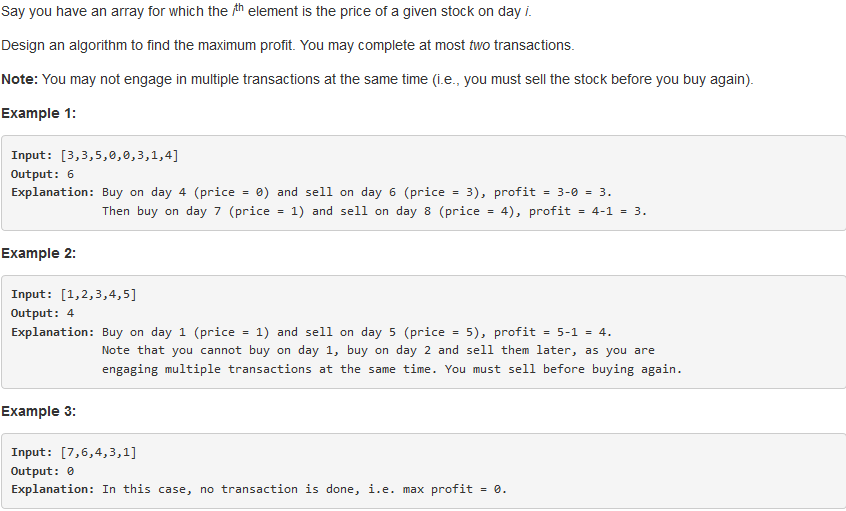
问题求解：

k = 2，则递推式变为：

T[i][2][0] = max(T[i - 1][2][0]，T[i - 1][2][1] + prices[i])

T[i][2][1] = max(T[i - 1][2][1]，T[i - 1][1][0] - prices[i])

T[i][1][0] = max(T[i - 1][1][0]，T[i - 1][1][1] + prices[i])

T[i][1][1] = max(T[i - 1][1][1]，0 - prices[i])

对空间复杂度进行优化，可以在<O(n)，O(1)>完成求解。

    public int maxProfit(int[] prices) {
        int Ti20 = 0;
        int Ti21 = Integer.MIN_VALUE;
        int Ti10 = 0;
        int Ti11 = Integer.MIN_VALUE;
        for (int price : prices) {
            Ti20 = Math.max(Ti20, Ti21 + price);
            Ti21 = Math.max(Ti21, Ti10 - price);
            Ti10 = Math.max(Ti10, Ti11 + price);
            Ti11 = Math.max(Ti11, -price);
        }
        return Math.max(Ti20, Ti21);
    }

188. Best Time to Buy and Sell Stock IV

问题描述：

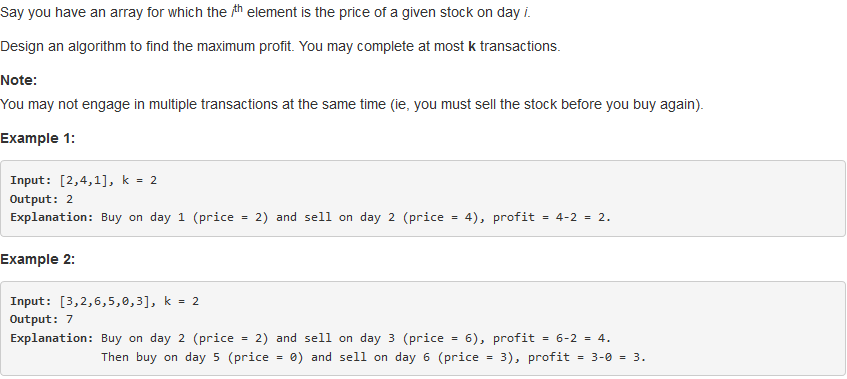
问题求解：

回到最初讨论的问题，k是一个有限常数，则递推式为：

T[i][k][0] = max(T[i - 1][k][0]，T[i - 1][k][1] + prices[i])

T[i][k][1] = max(T[i - 1][k][1]，T[i - 1][k - 1][0] - prices[i])

需要注意到，当k > n / 2的时候，k就可以看作是INF，因为同一天卖出买入等效于这一天没有操作，所以最多的k次有效交易为n / 2，超过了这个数就有废操作了。

另外，此时每一天有k个状态，所以可以用两个k + 1大小的数组来保存状态量，最终在<O(kn)，O(k)>完成求解。

    public int maxProfit(int k, int[] prices) {
        if (k > prices.length >>> 1) {
            int Tik0 = 0;
            int Tik1 = Integer.MIN_VALUE;
            for (int price : prices) {
                int tmp = Tik0;
                Tik0 = Math.max(Tik0, Tik1 + price);
                Tik1 = Math.max(Tik1, tmp - price);
            }
            return Math.max(Tik0, Tik1);
        }

        int[] Tik0 = new int[k + 1];
        int[] Tik1 = new int[k + 1];
        Arrays.fill(Tik1, Integer.MIN_VALUE);
        for (int price : prices) {
            for (int i = k; i > 0; i--) {
                Tik0[i] = Math.max(Tik0[i], Tik1[i] + price);
                Tik1[i] = Math.max(Tik1[i], Tik0[i - 1] - price);
            }
        }
        return Math.max(Tik0[k], Tik1[k]);
    }

本题如果使用原始的递推式来解的话可以这么修改，因为-1在数组中是没有办法进行初始化的，于是我们可以这样定义递推公式：

dp[i][k][0] ：经过了i天并使用了k次交易后剩余0股的最大利润；

dp[i][k][1] ：经过了i天并使用了k次交易后剩余1股的最大利润；

于是dp[0][k][0] = 0；dp[0][k][1] = Integer.MIN_VALUE，这样就可以避免上述的问题。

    public int maxProfit(int k, int[] prices) {
        int n = prices.length;
        if (k >= n / 2) return helper(prices);
        int[][][] dp = new int[k + 1][n + 1][2];
        for (int i = 0; i <= n; i++) {
            dp[0][i][0] = 0;
            dp[0][i][1] = Integer.MIN_VALUE;
        }
        for (int i = 0; i <= k; i++) {
            dp[i][0][0] = 0;
            dp[i][0][1] = Integer.MIN_VALUE;
        }
        for (int i = 1; i <= k; i++) {
            for (int j = 1; j <= n; j++) {
                dp[i][j][0] = Math.max(dp[i][j - 1][0], dp[i][j - 1][1] + prices[j - 1]);
                dp[i][j][1] = Math.max(dp[i][j - 1][1], dp[i - 1][j - 1][0] - prices[j - 1]);
            }
        }
        return dp[k][n][0];
    }

    private int helper(int[] prices) {
        int tik0 = 0;
        int tik1 = Integer.MIN_VALUE;
        for (int price : prices) {
            int tmp = tik0;
            tik0 = Math.max(tik0, tik1 + price);
            tik1 = Math.max(tik1, tmp - price);
        }
        return tik0;
    }

【注意】

这次在解决这个问题的时候出现了MLE的情况，原本以为是三维的数组超了内存，但是实际是没有对k的大小进行判断。

所以这里对k的大小进行提前判断是必要的，如果不判断，直接使用dp那么就会MLE。

这里还有一个问题需要考虑，就是一般来说，我们会将问题规约到可以解决的更小的问题上，而且一般是对k进行外层遍历。

换言之，就是和问题给的方式相同，我们先算k次交易各个天数的最大结果，之后下一轮计算k + 1次的，这里没有这么计算的原因很简单，就是在递推式中第i天的交易总额和第i - 1天的k + 1次交易也有关联，也就是在子问题中k的规模并没有更小，所以必须针对每一天算出所有的k后在计算下一天。

    public int maxProfit(int k, int[] prices) {
        int days = prices.length;
        if (k >= days / 2) return helper(prices);
        int[][] dp = new int[k + 1][2];
        for (int i = 0; i <= k; i++) {
            dp[i][0] = 0;
            dp[i][1] = Integer.MIN_VALUE;
        }
        for (int price : prices) {
            for (int i = 1; i <= k; i++) {
                dp[i][0] = Math.max(dp[i][0], dp[i][1] + price);
                dp[i][1] = Math.max(dp[i][1], dp[i - 1][0] - price);
            }
        }
        return Math.max(dp[k][0], dp[k][1]);
    }
    
    private int helper(int[] prices) {
        int Tik0 = 0;
        int Tik1 = Integer.MIN_VALUE;
        for (int price : prices) {
            Tik0 = Math.max(Tik0, Tik1 + price);
            Tik1 = Math.max(Tik1, Tik0 - price);
        }
        return Math.max(Tik0, Tik1);
    }

posted @ 2018-04-30 21:02 hyserendipity 阅读(277) 评论(0) 编辑收藏举报

刷新页面返回顶部

hyserendipity

动态规划-Stock Problem

公告