全排列 Permutation
2018-03-05 15:24:30
一、无重复数组的全排列
问题描述:

问题求解:
解法一、Perm算法
使用经典的Perm算法进行求解即可,需要注意的是,最后不能直接使用Arrays.aslist()函数进行数组和集合的转换,首先这个函数只使用于引用类型,如果是int类型这种方法就不再适用了。
另外,必须在添加的时候新建一个List,如果只是单纯将当前的nums添加进去,那么根据Java的定义,引用的值会在之后持续的发生修改,最后导致所有的工作都失效。
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
perm(res, nums, 0);
return res;
}
void perm(List<List<Integer>> res, int[] nums, int index) {
if (index == nums.length - 1) {
ArrayList<Integer> ls = new ArrayList<>();
for (int i : nums) {
ls.add(i);
}
res.add(ls);
}
else {
for (int i = index; i < nums.length; i++) {
int tmp = nums[i];
nums[i] = nums[index];
nums[index] = tmp;
perm(res, nums, index + 1);
tmp = nums[i];
nums[i] = nums[index];
nums[index] = tmp;
}
}
}
void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
解法二:
使用一个visited数组来记录已经访问过的数字,并在之后不使用即可。
Perm算法有个缺点就是,Perm算法在不断的调整整个数组的顺序,这种变化在以后处理更为复杂的情况的时候会非常棘手。
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
helper(nums, new int[nums.length], new ArrayList<>(), res);
return res;
}
private void helper(int[] nums, int[] visited, List<Integer> cur, List<List<Integer>> res){
if (cur.size() == nums.length) res.add(new ArrayList<>(cur));
else {
for (int i = 0; i < nums.length; i++) {
if (visited[i] == 0) {
cur.add(nums[i]);
visited[i] = 1;
helper(nums, visited, cur, res);
visited[i] = 0;
cur.remove(cur.size() - 1);
}
}
}
}
二、有重复数组的全排列
问题描述:
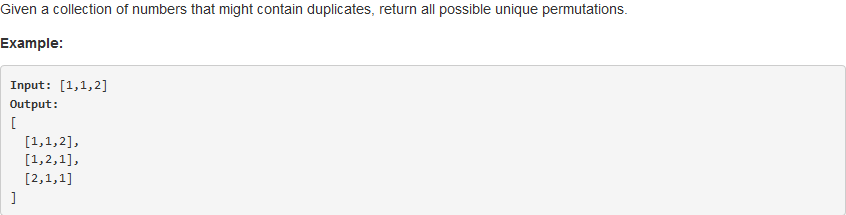
问题求解:
本题就不太适合使用Perm算法了,反复的修改数组的值总是一个非常不好的情况,我们希望在解空间搜索的过程中原数组是不变动的。
public List<List<Integer>> permuteUnique(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
helper(nums, new ArrayList<>(), new int[nums.length], res);
return res;
}
private void helper(int[] nums, List<Integer> cur,int[] visited, List<List<Integer>> res) {
if (cur.size() == nums.length) {
res.add(new ArrayList<>(cur));
}
else {
for (int i = 0; i < nums.length; i++) {
if (visited[i] == 1 || (i > 0 && nums[i] == nums[i - 1] && visited[i - 1] == 0)) continue;
cur.add(nums[i]);
visited[i] = 1;
helper(nums, cur, visited, res);
visited[i] = 0;
cur.remove(cur.size() - 1);
}
}
}
三、Permutation Sequence
问题描述:

问题求解:
方法一:
遍历解空间,值得注意的是,这里是没有办法使用Perm算法的,因为Perm算法会改变数字的位置,因此只能只用加used[]的解法。
public String getPermutation(int n, int k) {
int[] nums = new int[n];
for (int i = 0; i < n; i++) nums[i] = i + 1;
List<Integer> res = helper(nums, new int[n], new int[]{k}, new ArrayList<>());
StringBuffer sb = new StringBuffer();
for (int i = 0; i < res.size(); i++) sb.append(res.get(i));
return sb.toString();
}
private List<Integer> helper(int[] nums, int[] used, int[] k, List<Integer> res) {
if (k[0] <= 0) return null;
if (res.size() == nums.length) {
k[0]--;
if (k[0] == 0) return res;
else return null;
}
for (int i = 0; i < nums.length; i++) {
if (used[i] == 0) {
used[i] = 1;
res.add(nums[i]);
if (helper(nums, used, k, res) != null) return res;
res.remove(res.size() - 1);
used[i] = 0;
}
}
return null;
}
方法二:
方法二是一种数学的方法,由于题目最后的输出是按照字典序进行输出的,因此可以通过计算每个数字的可能后缀个数来计算当前位置的数字应该是多少。
public String getPermutation(int n, int k) {
List<Integer> ls = new ArrayList<>();
for (int i = 1; i <= n; i++) ls.add(i);
StringBuffer sb = new StringBuffer();
for (int i = 1; i <= n; i++) {
int cnt = factor(n - i);
int idx = (int)Math.ceil(k * 1.0 / cnt) - 1;
k -= idx * cnt;
sb.append(ls.get(idx));
ls.remove(idx);
}
return sb.toString();
}
private int factor(int n) {
if (n <= 1) return 1;
return factor(n - 1) * n;
}
2019.04.19
public String getPermutation(int n, int k) {
Set<Integer> set = new HashSet<>();
for (int i = 1; i <= n; i++) set.add(i);
StringBuffer sb = new StringBuffer();
helper(set, k, sb);
return sb.toString();
}
private void helper(Set<Integer> set, int k, StringBuffer sb) {
if (set.size() == 1) sb.append(set.iterator().next());
else {
int n = set.size();
int cnt = 1;
for (int i = 1; i <= n - 1; i++) cnt *= i;
int idx = (int) Math.ceil(k * 1.0 / cnt) - 1;
List<Integer> tmp = new ArrayList<>(set);
Collections.sort(tmp);
int target = tmp.get(idx);
sb.append(target);
set.remove(target);
helper(set, k - cnt * idx, sb);
}
}
四、Next Permutation
问题描述:

问题求解:
public void nextPermutation(int[] nums) {
if (nums.length <= 1) return;
int idx = nums.length - 2;
while (idx >= 0 && nums[idx] >= nums[idx + 1]) idx--;
if (idx == -1) {
reverse(nums, 0, nums.length - 1);
return;
}
int i = nums.length - 1;
while (i >= 0 && nums[i] <= nums[idx]) i--;
swap(nums, i, idx);
reverse(nums, idx + 1, nums.length - 1);
}
public void reverse(int[] nums, int begin, int end) {
while (begin < end) {
swap(nums, begin, end);
begin++;
end--;
}
}
public void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
2019.04.20
可以从另一个角度看问题,本题的本质是在找每个数字左侧第一个比它小的数,同时,这个pair中i,j都要尽可能的大。
毫无疑问,求左侧第一个比它小的数字可以使用单调堆栈在O(n)的时间复杂度求解,得到这个关键信息后,就可以直接求解了。
public void nextPermutation(int[] nums) {
if (nums.length < 2) return;
int pi = -1;
int pj = -1;
Stack<int[]> stack = new Stack<>();
for (int i = 0; i < nums.length; i++) {
while (!stack.isEmpty() && stack.peek()[0] >= nums[i]) stack.pop();
if (!stack.isEmpty() && stack.peek()[1] >= pi) {
pi = stack.peek()[1];
pj = i;
}
stack.push(new int[]{nums[i], i});
}
if (pi == -1) Arrays.sort(nums);
else {
int tmp = nums[pi];
nums[pi] = nums[pj];
nums[pj] = tmp;
Arrays.sort(nums, pi + 1, nums.length);
}
}




