哈夫曼树与哈夫曼编码

2018-03-02 15:03:37

编码问题是计算机科学乃至EE中的一个核心的问题，最基础的编码方式是采用等长的编码，比如计算机中的字符的编码就是采用等长的8位，即一个字节进行的编码。

但是在实际生活中，每个字符出现的频率是不同的，因此，如果我们采用不等长编码，将出现频率高的字符采用较短的编码，对出现频率低的字符采用较长的编码，就可以实现更高效和节省的编码。

一、哈夫曼树

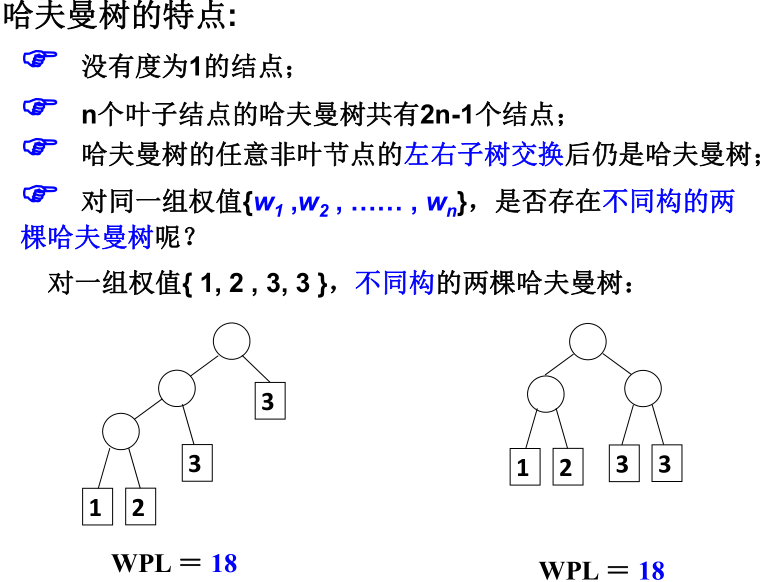
霍夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的路径长度是从树根到每一结点的路径长度之和，记为WPL=（W1*L1+W2*L2+W3*L3+...+Wn*Ln），N个权值Wi（i=1,2,...n）构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li（i=1,2,...n）。可以证明霍夫曼树的WPL是最小的。

1951年，霍夫曼和他在MIT信息论的同学得选择是完成学期报告还是期末考试。导师罗伯特·法诺出的学期报告题目是，查找最有效的二进制编码。由于无法证明哪个已有编码是最有效的，霍夫曼放弃对已有编码的研究，转向新的探索，最终发现了基于有序频率二叉树编码的想法，并很快证明了这个方法是最有效的。霍夫曼使用自底向上的方法构建二叉树，避免了次优算法香农-范诺编码的最大弊端──自顶向下构建树。

算法流程：

假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为：

(1) 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；

(2) 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；

(3)从森林中删除选取的两棵树，并将新树加入森林；

(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

typedef struct TreeNode *HuffmanTree;
struct TreeNode{
    int Weight;
    HuffmanTree Left, Right;
}

HuffmanTree Huffman( MinHeap H )
{   /*  假设H->Size 个权值已经存在H->Elements[]->Weight 里 */
    int i; HuffmanTree T;
    BuildMinHeap(H); /* 将H->Elements[] 按权值调整为最小堆*/
    for (i = 1; i < H->Size; i++) { /* 做H->Size-1 次合并*/
        T = malloc( sizeof( struct TreeNode) ); /* 建立新结点*/
        T->Left = DeleteMin(H);
        /* 从最小堆中删除一个结点 ， 作为新T 的左子结点*/
        T->Right = DeleteMin(H);
        /* 从最小堆中删除一个结点 ， 作为新T 的右子结点*/
        T->Weight = T->Left->Weight+T->Right->Weight;
        /* 计算新权值*/
        Insert( H, T ); /* 将新T 插入最小堆*/
    }
    T = DeleteMin(H);
    return T;
}

 

 

二、哈夫曼编码

问题：给定一段字符串，如何对字符进行编码 ，可以使得该字符串的编码存储空间最少？

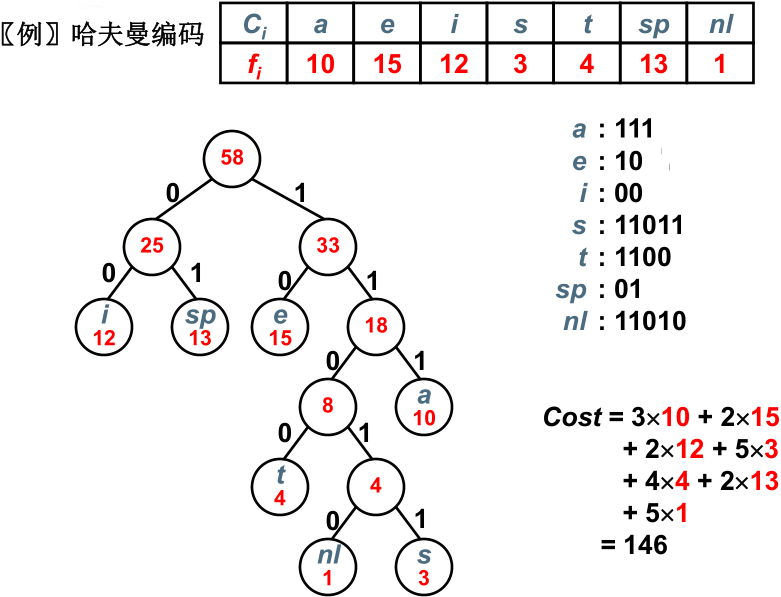
【例】假设有一段文本，包含58 个字符，并由以下7 个字符构：a ，e ，i， s ，t ，空格（sp），换行（nl）；这7个字符出现的次数不同。如何对这7个字符进行编码，使得总编码空间最少？
【分析】
（1）用等长ASCII 编码：58  ×8 = 464 位；
（2）用等长3 位编码：58  ×3 = 174 位；
（3）不等长编码：出现频率高的字符用的编码短些 ，出现频率低的字符则可以用较长的编码进行表示。

采用不定长编码编码最本初的问题就是如何避免二义性，在解释一段编码的时候如果有多于一种的解释，显然这种编码就是不可靠的。

经过证明只要任何字符的编码都不是另一字符编码的前缀，就可以避免二义性。

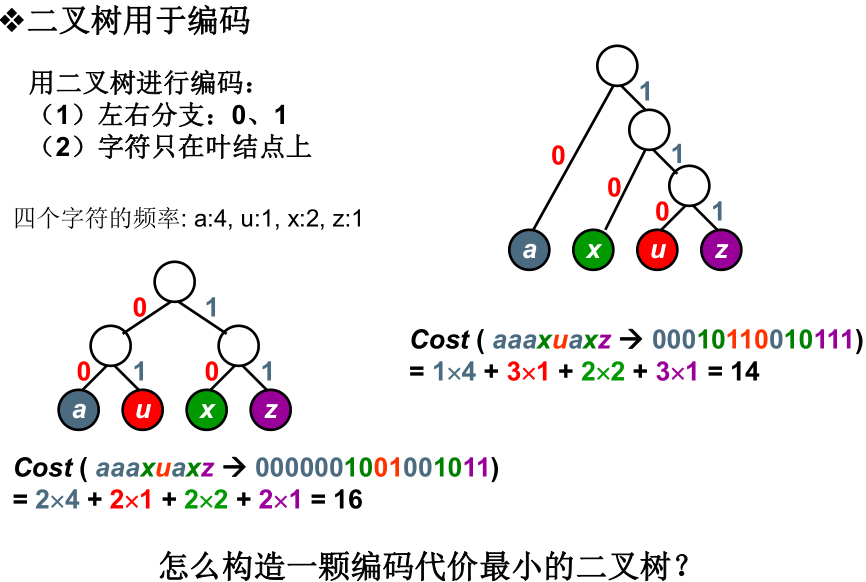
显然的是，只要字符出现在叶子结点就不能是另一个编码的前缀码，并且当前的编码问题本质上就是构造哈夫曼树。