随笔- 597 文章- 0 评论- 5 阅读- 35万

数学类题目

2018-01-20 14:46:51

判断一个数是否为完全平方数。（不允许使用库函数）

方法一、使用前n个奇数和为n^2的结论

1+3+5+...2n-1 = n*n，因此我们只需要不断的减奇数知道小于等于0，若等于0，则为完全平方数，若不为0，则非完全平方数。

public boolean isPerfectSquare(int num) {
     int i = 1;
     while (num > 0) {
         num -= i;
         i += 2;
     }
     return num == 0;
 }

方法二、二分查找法

使用二分法不断查找自乘等于给定数的数，若存在则为完全平方数，若不存在，则非完全平方数。

public boolean isPerfectSquare(int num) {
        int low = 1, high = num;
        while (low <= high) {
            long mid = (low + high) >>> 1;
            if (mid * mid == num) {
                return true;
            } else if (mid * mid < num) {
                low = (int) mid + 1;
            } else {
                high = (int) mid - 1;
            }
        }
        return false;
    }

方法三、牛顿迭代法

从给定数开始使用牛顿迭代法，每次取整，若为完全平方数，例如16，则必定会得到4；若为非完全平方数17，则会在取整的过程中得到3。

public boolean isPerfectSquare(int num) {
        // 必须使用long，目的是防止越界<br>　　　　 // 当num = 0x7fffffff 时，如果使用int会发生越界<br>　　　　 long x = num;
        while (x * x > num) {
            x = (x + num / x) >> 1;
        }
        return x * x == num;
}

杨辉三角问题

问题描述：

问题求解：

杨辉三角的递推式显然是b[i][n] = b[i-1][n] + b[i-1][n-1]。如果是从1开始迭代，那么就会导致下一个数的迭代比较麻烦，因为会覆盖当前数，当然了，这种覆盖可以通过保存进行解决，但是更精巧的解决方案是从末尾向前进行迭代，这样就很巧妙的避免了覆盖问题。

public List<Integer> getRow2(int rowIndex) {
      Integer[] result =  new Integer[rowIndex + 1];
      Arrays.fill(result, 0);
      result[0] = 1;
      for(int i = 1; i < rowIndex + 1; i++)
        for(int j = i; j >= 1; j--)
          result[j] += result[j - 1];
      return Arrays.asList(result);
}

n！阶乘的末尾0的个数

显然的是只需要计算其中5个因子个数即可，因为10 = 2*5，而5的因子数肯定要远远小于2的个数。但是如何计算5的因子数还是有技巧的。

首先是brute force的解法，就是简单的从5-n对每个数中5的个数进行计数。这种方法的时间复杂度为O(n)。

巧妙一点的解法就是，先计算n/5，得到那些提供了一个5的数的个数，然后计算n/25，得到那些提供了2个5的数的个数...依次类推。

代码使用递归的话，也相当简洁，时间复杂度为O(lgn)。

1	`return` `n ==` `0` `?` `0` `: n /` `5` `+ trailingZeroes(n /` `5);`

三角形数

一定数目的点或圆在等距离的排列下可以形成一个等边三角形，这样的数被称为三角形数。比如10个点可以组成一个等边三角形，因此10是一个三角形数：

一开始的18个三角形数是1、3、6、10、15、21、28、36、45、55、66、78、91、105、120、136、153、171、190、210、231、253……

一种检验正整数x是否三角形数的方法，是计算：

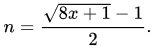
若n为整数则x为第n个三角数。

问题描述：现给一个数，判断其为第几个三角数。

问题求解：

方法一、最直观的想法是求解公式（1+x）x = 2n。使用牛顿迭代法可以进行求解，最后取整即可。这种方法效率不高。

方法二、二分查找法

使用二分查找法要特别注意数值越界的问题，一是mid = L + （R - L）/2，如果写成mid = （L + R）/2，则可能出现整形越界问题。

二是在判断中要使用0.5*mid*mid + 0.5*mid<n，如果写成（mid+1）*mid<2*n，那么（mid+1）*mid可能会越界，2*n也可能会越界。

public static int arrangeCoins(int n) {
    int L = 0;
    int R = n;
    while(L <= R) {
        int mid = L + (R - L)/2;
        if(0.5*mid*mid + 0.5*mid<n) L = mid + 1;
        else if(0.5*mid*mid + 0.5*mid>n) R = mid - 1;
        else return mid;
    }
    return L - 1;
}

方法三、公式法

public int arrangeCoins(int n) {
    return (int) ((Math.sqrt(1 + 8.0 * n) - 1) / 2);
}

回文整数问题

问题描述：判断一个整数是否为回文数字，注意不能使用额外的空间，不能转成String。

问题求解：解决方法很有创造性，简单来说就是把原数字的后一半数字倒序组成新的整数，然后加之判断。

public boolean isPalindrome(int x) {
    if (x<0 || (x!=0 && x%10==0)) return false;
    int rev = 0;
    while (x>rev){
        rev = rev*10 + x%10;
        x = x/10;
    }
    return (x==rev || x==rev/10);
}

十进制转十六进制

问题求解：将十进制转成16进制，不用再去进行什么辗转相除求余数在reverse啦，直接使用位运算，利用计算机底层的二进制就可以很方便的完成进制的转换。

// 思路本质上是一样的，但是使用位运算显得更简洁
// 另外，由于负数，例如-1，在Java中本身就是以二进制补码进行表示的，所以直接运算即可
// 可以说是非常巧妙的
public String toHex(int num) {
    if (num == 0) return "0";
    char[] map = new char[]{'0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'a', 'b', 'c', 'd', 'e', 'f'};
    StringBuilder res = new StringBuilder();
    while (num != 0) {
        res.insert(0, map[num & 0b1111]);
        num = num >>> 4;
    }
    return res.toString();
}

大整数求和

问题描述：将两个非负整数num1，num2进行求和，其中num1，num2都以字符串的形式给出。

问题求解：

public String addStrings(String num1, String num2) {
    if (num1.length() < num2.length()) return addStrings(num2, num1);
    char[] n1 = num1.toCharArray(), n2 = num2.toCharArray();
    int m = n1.length, n = n2.length;
    int carry = 0, i = 1, sum = 0;
    while (i <= n) {
        sum = n1[m - i] + n2[n - i] - '0' * 2 + carry;
        carry = sum / 10;
        n1[m - i] = (char) (sum % 10 + '0');
        i++;
    }
    while (carry > 0 && i <= m) {
        sum = n1[m - i] + carry - '0';
        carry = sum / 10;
        n1[m - i] = (char) (sum % 10 + '0');
        i++;
    }
    return carry == 0 ? new String(n1) : "1" + new String(n1);
}

平方数的和

问题描述：给一个非负整数，判断其是否可以用两个平方数求和得到。

问题求解：显然可以brute force，遍历求解。但是使用二分法会效率更高。

public boolean judgeSquareSum(int c) {
    if (c < 0) {
        return false;
    }
    int left = 0, right = (int)Math.sqrt(c);
    while (left <= right) {
        int cur = left * left + right * right;
        if (cur < c) {
            left++;
        } else if (cur > c) {
            right--;
        } else {
            return true;
        }
    }
    return false;
}

第三大的数

问题描述：寻找数组中第三大的数，如果不存在返回最大的数。

问题求解：O(n)内找到第三大的数肯定是不断的比较，问题就是一、如何初始化，如果初始化为Integer.MIN_VALUE，那么对于第三大的数正好是MIN_VALUE的如何处理就会很成问题，二、如何很好的解决同样大的问题。

public int thirdMax(int[] nums) {
    Integer max1 = null;
    Integer max2 = null;
    Integer max3 = null;
    for (Integer n : nums) {
        if (n.equals(max1) || n.equals(max2) || n.equals(max3)) continue;
        if (max1 == null || n > max1) {
            max3 = max2;
            max2 = max1;
            max1 = n;
        } else if (max2 == null || n > max2) {
            max3 = max2;
            max2 = n;
        } else if (max3 == null || n > max3) {
            max3 = n;
        }
    }
    return max3 == null ? max1 : max3;
}

2019-09-05

public int thirdMax(int[] nums) {
    int a = nums[0];
    Integer b = null;
    Integer c = null;
    for (int i = 1; i < nums.length; i++) {
        if (nums[i] >= a) {
            if (nums[i] == a) continue;
            c = b;
            b = a;
            a = nums[i];  
        }
        else if (b == null || nums[i] >= b) {
            if (b != null && nums[i] == b) continue;
            c = b;
            b = nums[i];
        }
        else if (c == null || nums[i] > c) {
            c = nums[i];
        }
    }
    return c == null ? a : c;
}

数素数

问题描述：对小于n的素数个数计数。

问题求解：如果对每个数进行判断，则需要O(n*n)，显然还是比较耗时的，并且，每次对新的数字都要重复判断，算法效率很低。

针对素数计数的问题，或者给定区间的素数求解，可以采用筛选法，能够高效的完成多个素数的获取。

public int countPrimes(int n) {
    boolean[] notPrime = new boolean[n];
    int count = 0;
    for (int i = 2; i < n; i++) {
        if (notPrime[i] == false) {
            count++;
            for (int j = 2; i*j < n; j++) {
                notPrime[i*j] = true;
            }
        }
    }
    return count;
}

最大回文数

问题描述：找到最大的由两个n位数字乘积得到的回文数，最后的结果对1337取mod。例如，9009 = 99 * 91，9009 % 1337 = 987。

问题求解：首先找到最大的可能回文数字，然后递减循环遍历寻找。

public int largestPalindrome(int n) {
    if (n == 1) return 9;
    long maxNum = (long) Math.pow(10, n) - 1;
    long minNum = (long) Math.pow(10, n - 1);
    long maxProduct = maxNum * maxNum;
    long firstHalf = maxProduct / (long) Math.pow(10, n);
 
    while (true) {
        long candidate = palindrome(firstHalf--);
        for (long i = maxNum; i > candidate / i; i--) {
            if (candidate % i == 0 && candidate / i >= minNum) {
                return (int) (candidate % 1337);
            }
        }
    }
}
 
public long palindrome(long num) {
    String str = num + new StringBuilder().append(num).reverse().toString();
    return Long.parseLong(str);
}

Counting Bits

问题描述：给一个非负整数，返回[0,num]里每个数的二进制表示的1的个数。要求算法的复杂度为O(n)/O(n)。

问题求解：很容易想到一个O(n*sizeof(Integer))的解法，也就是对每个整数分别求解其中的一的个数。但是这里要求严格的O(n)，于是这种暴力的每个单个求解的方法就不是很合适了。

问题的关键其实就是如何利用已经求解出来的前面的1的个数，事实上利用一个trick：f(n) = f(n >> 1) + (n&1)，就可以建立当前数和之前求解数的联系。

public int[] countBits(int num) {
    int[] res = new int[num + 1];
    for(int i = 1; i <= num; i++) res[i] = res[i>>1] + (i&1);
    return res;
}

Product of Array Except Self

问题描述：对于给定的数组nums，其中output[i]等于其他各个除了自己的乘积。要求：O(n)/O(1)，不允许用除法。

问题求解：首先用除法的解法不言而喻，且是O(n)/O(1)，但已经明确规定不允许使用除法，故排除。

一个很实用的方法是构造两个数组分别存储左乘积和右乘积：

[1, a1, a1*a2, a1*a2*a3]
[a2*a3*a4, a3*a4, a4, 1]

思路就是这样的思路，具体实现上，我们可以用一些技巧使空间复杂度降到O(1)。

public int[] productExceptSelf(int[] nums) {
    int[] res = new int[nums.length];
    res[0] = 1;
    for (int i = 1; i < nums.length; i++) {
        res[i] = res[i - 1] * nums[i - 1];
    }
    int tmp = 1;
    for (int i = nums.length - 2; i >= 0 ; i--) {
        tmp *= nums[i + 1];
        res[i] *= tmp;
    }
    return res;
}

StackOverflow上给出了一种递归的解决方案，很是巧妙，这里对其进行一些rewrite，使其更容易理解。

如果单纯的让你求数组[i，nums.length - 1]的乘积，这是很容易使用递归求解的：

f[i] = f[i + 1] * nums[i] where i < nums.length - 1;

f[i] = nums[i] where i = nums.length - 1;

在此基础上，如果在形参中引入前n项的乘积，便可以解决这个问题。值得注意的是，这种递归的解法要特别注意栈溢出问题。虽然该题可以使用这种解法，但是在leecode上会报错（Stack Overflow）。

public static int multiply(int[] nums, int pre, int index, int N) {
    if(index == N - 1) {
        int cur = nums[index];
        nums[index] = pre;
        return cur;
    }
    else {
        int post = multiply(nums, pre * nums[index], index + 1, N);
        int cur = nums[index];
        nums[index] = post * pre;
        return cur * post;
    }
}

下一个更大的数

问题描述：

给你两个数组（没有重复）nums1和nums2，其中nums1的元素是nums2的子集。找到所有在nums2相应地nums1的元素的下一个更大的数字。
在nums1一个数x的下一个更大的数字是其在nums2右侧的第一个较大的数字。如果不存在，则输出-1。

问题求解：

很容易想到一个基于HashMap的O(n^2)的解法，具体来说就是遍历nums2，对每一个数找寻其后面的比他大的数字并将之保存在HashMap中，然后再遍历nums1从Map中取数值即可。

public int[] nextGreaterElement(int[] nums1, int[] nums2) {
    HashMap<Integer, Integer> map = new HashMap<>();
    for (int i = 0; i < nums2.length; i++) {
        int j = i+1;
        while(j<nums2.length&&nums2[j]<nums2[i]) j++;
        if(j == nums2.length) map.put(nums2[i], -1);
        else map.put(nums2[i], nums2[j]);
    }
    for (int i = 0; i < nums1.length; i++) {
        nums1[i] = map.get(nums1[i]);
    }
    return nums1;
}

事实上，在遍历nums2构造Map的时候，可以使用Stack将时间复杂度降到O（n）。具体来说，stack中保存了一个降序的子序列，如果当前的数字比栈顶的元素还要大的话，则将栈中元素弹出，并且弹出的元素的后一个更大的值即是当前的值。

// 以上使用的解法是一种比较naive的brute force的解法
// 显然其时间复杂度为O(n^2)
// 有一种非常精妙的解法可以在O(n)的时间复杂度完成上述的工作
// 可以使用Stack来维护一个递减(可以等于)的子序列，如果当前的数比栈顶元素大
// 那么说明栈中比当前元素小的的下一个大值就是他
public int[] nextGreaterElement2(int[] findNums, int[] nums) {
    Map<Integer, Integer> map = new HashMap<>(); // map from x to next greater element of x
    Stack<Integer> stack = new Stack<>();
    for (int num : nums) {
        while (!stack.isEmpty() && stack.peek() < num)
            map.put(stack.pop(), num);
        stack.push(num);
    }
    for (int i = 0; i < findNums.length; i++)
        findNums[i] = map.getOrDefault(findNums[i], -1);
    return findNums;
}

问题扩展：

给定一个圆形数组（最后一个元素的下一个元素是数组的第一个元素），为每个元素打印Next Greater Number。数字x的下一个较大数字是数组中下一个遍历顺序的第一个更大的数字，这意味着您可以循环搜索以找到下一个更大的数字。如果不存在，则输出-1。

问题求解：

总体的思路是一样的，只是在实现的需要注意一个小问题就是环形的处理，我们可以这样解决这个问题，对原数组拼接一个原数组，那么如果遍历这个数组，就等同于环形数组。然后，还有一个事情需要明确，那就是这里拼接后，也只需要求前n个数的下一个最大的数字。另外，栈中保存的是数组的下标，这样的好处就是在生成结果数组的时候可以很方便的对对应的下标进行填写。

public int[] nextGreaterElements(int[] nums) {
    int n = nums.length;
    int[] res = new int[nums.length];
    Arrays.fill(res, -1);
    Stack<Integer> stack = new Stack<>();
    for (int i = 0; i < 2 * n; i++) {
        int num = nums[i % n];
        while (!stack.isEmpty() && nums[stack.peek()] < num) {
            res[stack.pop()] = num;
        }
        if (i < n) stack.push(i);
    }
    return res;
}

数组中两个数的异或的最大值

问题描述：

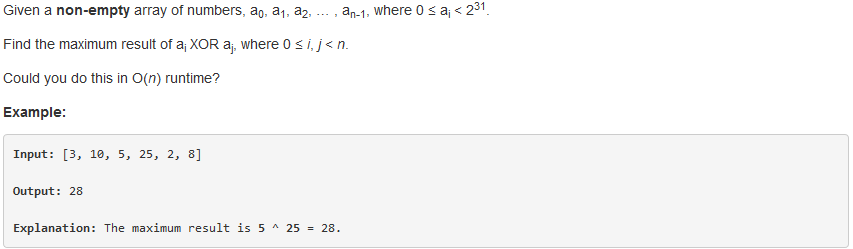
问题求解：

方法一、使用掩码的方式逐个计算从高到底计算是否当前位置有可能产生1。

public int findMaximumXOR(int[] nums) {
    int res = 0;
    int mask = 0;
    for (int i = 31; i >= 0; i--) {
        mask = mask | (1 << i);
        HashSet<Integer> set = new HashSet<>();
        for (int num : nums) {
            set.add(num & mask);
        }
        int tmp = res | (1 << i);
        for (int num : set) {
            if (set.contains(tmp ^ num)) res = tmp;
        }
    }
    return res;
}

方法二、运用数据结构Trie树来简化问题，将数字的各个位存储成Trie树，然后对每个数值进行计算，看其能够达到的最大的异或值是多少，取最大。

class TrieNode {
    TrieNode[] child;
 
    TrieNode() {
        child = new TrieNode[2];
    }
}
 
public int findMaximumXOR(int[] nums) {
    int res = 0;
    TrieNode root = new TrieNode();
    for (int num : nums) {
        TrieNode cur = root;
        for (int i = 31; i >= 0; i--) {
            int bit = (num >> i) & 1;
            if (cur.child[bit] == null) cur.child[bit] = new TrieNode();
            cur = cur.child[bit];
        }
    }
 
    for (int num : nums) {
        TrieNode cur = root;
        int curSum = 0;
        for (int i = 31; i >= 0; i--) {
            int bit = (num >> i) & 1;
            if (cur.child[bit ^ 1] != null) {
                cur = cur.child[bit ^ 1];
                curSum += (1 << i);
            }
            else cur = cur.child[bit];
        }
        if (curSum > res) res = curSum;
    }
 
    return res;
}

主元素问题

问题描述：数组中包含一个个数大于总个数一半的数，找出这个数。

问题求解：使用排序，然后取中位数是最朴素的思想，时间复杂度O(nlogn)。

主元素问题有个很经典的解法，就是Boyer-Moore Majority Vote Algorithm（摩尔投票算法）。这个算法是一个典型的流处理算法，其时间复杂度为O(n)。

public int majorityElement(int[] num) {
    int major=num[0], count = 1;
    for(int i=1; i<num.length;i++){
        if(count==0){
            count++;
            major=num[i];
        }else if(major==num[i]){
            count++;
        }else count--;          
    }
    return major;
}

When count != 0 , it means nums[1…i - 1] has a majority,which is major in the solution.
When count == 0 , it means nums[1…i - 1] doesn’t have a majority, so nums[1…i - 1] will not help nums[1…n].And then we have a subproblem of nums[i…n].

整数破裂

问题描述：

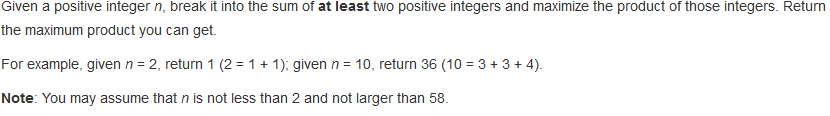
问题求解：

方法一、最容易想到的就是使用DP来对之前得到的值进行保存。基本上需要将近O(n^2)的时间复杂度。

public int integerBreak(int n) {
    int[] d = new int[60];
    d[1] = 1;
    d[2] = 1;
 
    for (int i = 3; i <= 58; i++) {
        for (int j = 1; j * 2 <= i; j++) {
            int tmp1 = d[j] > j ? d[j] : j;
            int tmp2 = d[i - j] > i - j ? d[i - j] : i - j;
            d[i] = Math.max(d[i], tmp1 * tmp2);
        }
    }
 
    return d[n];
}

方法二、Do Some Math.在本题中使用DP的时候应该已经意识到了，在选择是否使用DP保存的值的时候需要比较分裂后的值和当前的数值那个更大。其实，我们可以从数学上证明得到n在什么范围的时候分裂的结果肯定大于其自身的值。

考虑一分为二的情况，显然均分的情况得到的乘积最大，并且通过计算可以得到n>4的时候总是分裂的结果更大，因此，我们可以知道对所有的大于4的整数都要进一步的分解，直到其小于等于4。换句话说，就是最后分裂的结果中只存在2，3。又因为3 * 3 > 2 * 2 * 2。也就是说任何大于等于三个2都可以使用更大的3来代替，因此，我们需要尽量分解更多的3。事实上，最后的结果中只有至多2个2。基于这种思想，可以得到O(n)的解法。

public int integerBreak(int n) {
    if(n==2) return 1;
    if(n==3) return 2;
    int product = 1;
    while(n>4){
        product*=3;
        n-=3;
    }
    product*=n;
     
    return product;
}

Count Numbers with Unique Digits

问题描述：

问题求解：

设f(n)是长度为1的符合条件的个数。

则f(1) = 10；

f(2) = 9 * 9，首先首位可取1 - 9，末位可取剩下的位加上0；

f(3) = 9 * 9 * 8，道理很简单，现在对于末位只有8个可选数字了；

...

对于f(10) = 9 * 9 * 8 ... * 1。且对于所有的长度大于10的都为0。

public int countNumbersWithUniqueDigits(int n) {
    int[] map = new int[11];
    map[0] = 1;
    map[1] = 10;
    int num = 9;
    for (int i = 2; i <= 10; i++) {
        num *= (9 + 2 - i);
        map[i] = map[i - 1] + num;
    }
    return n > 10 ? map[10] : map[n];
}

分数到循环十进制

问题描述：

问题求解：

首先从大方向上来分析这条题目，既然是分数转小数，那么就只有两种可能，一是有限小数，二是无限循环小数。无限不循环小数是不可能存在的，因为这里是有理数，转成小数也是有理数。对于有限小数很容易解答，主要是对于循环小数，如何进行判断。事实上，对于循环小数，我们只需要判断每次的被除数，如果被除数已经出现过了，那么就势必会引起循环，因此我们只需要利用一个HashMap将被除数及其商的位置存储下来，下次碰到同样的，直接判循环即可。

当然，对于这类的算数问题，还需要解决一下最大值问题，简单的说就是当分子或分母取abs的时候，如果是Integer.MIN那么就会overflow，所以，需要对他们转成long进行运算。

public String fractionToDecimal(int numerator, int denominator) {
    if (denominator == 0) return "";
    if (numerator == 0) return "0";
    StringBuffer res = new StringBuffer();
    HashMap<Long, Integer> map = new HashMap<>();
    String c = (numerator > 0) ^ (denominator > 0) ? "-" : "";
    res.append(c);
    long num = Math.abs((long) numerator);
    long den = Math.abs((long) denominator);
    res.append(num / den);
    num %= den;
    if (num == 0) return res.toString();
    res.append(".");
    map.put(num, res.length());
    while (num != 0) {
        num *= 10;
        res.append(num / den);
        num %= den;
        if (map.containsKey(num)) {
            res.insert(map.get(num), "(");
            res.append(")");
            break;
        }
        else map.put(num, res.length());
    }
    return res.toString();
}