树 & 二叉树
2018-01-04 19:13:46
一、树
在计算机科学中,树(英语:tree)是一种数据结构,用来模拟具有树状结构性质的数据集合。它是由n(n>0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
客观世界中有很多具有层次关系的事物:
- 人类的社会家谱
- 社会组织结构
- 图书管理信息
类似这种层次结构就非常适用使用树来表示。
使用树的结构有很多有点,比如更形象的表述了层次关系,并且可以加速查找。
- 树的定义:
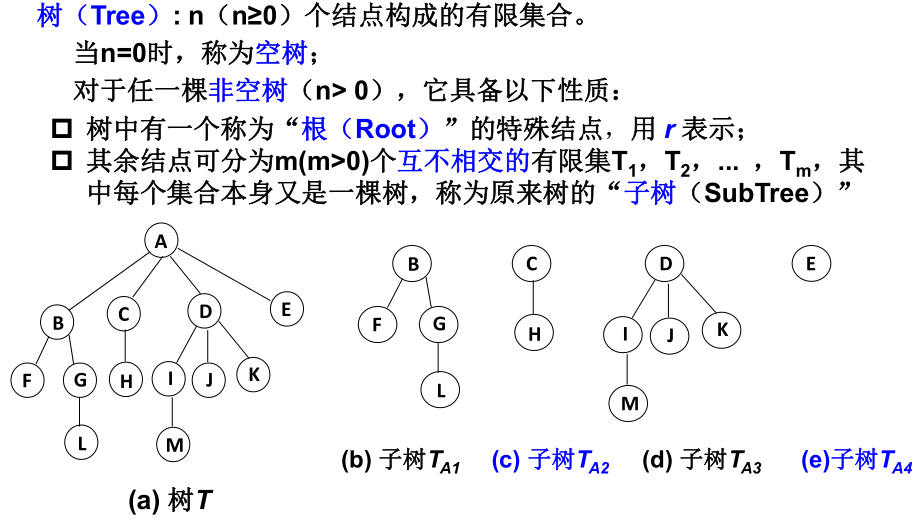
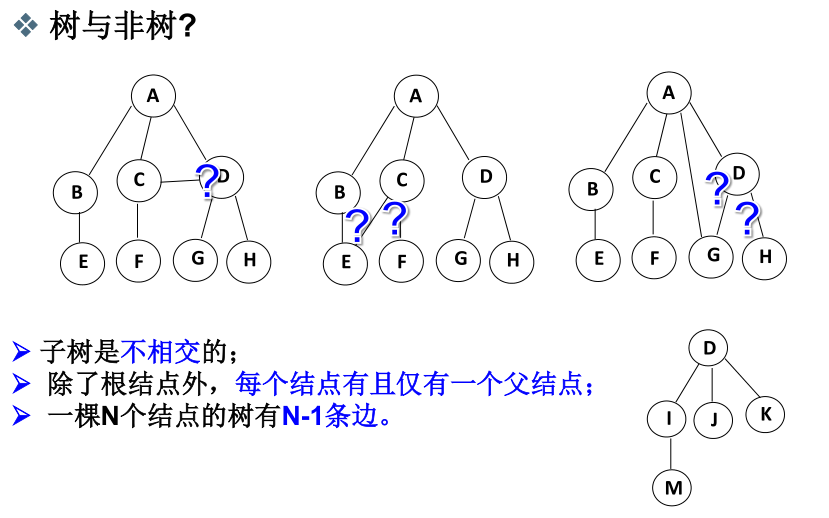
- 树的一些术语:


比如这里的L,M的深度就是4,因为他们在第4层。
- 树的表示:
1)链表存储
每个结点保存有一个指向其儿子结点的指针。这种方法为了程序的统一性,那么对于n个结点的树,就会产生3n个的指针树,也就是3n的边树,事实上,一颗树显然只有n-1条边,所以会有2n+1个指针为空,这就造成了空间的浪费。
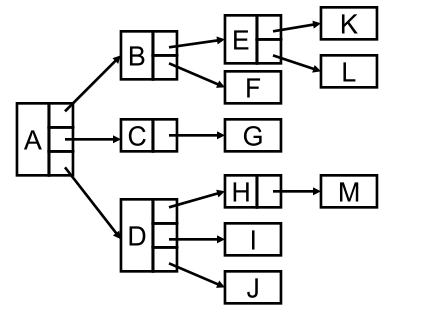
2)儿子-兄弟表示法
每个结点有两个指针,第一个指针指向他的第一个儿子,第二个指针指向他的兄弟,这样就可以组织好一个树,并且这种结构产生的指针为2n,那么对于n-1条边,总共浪费了n+1个指针空间,浪费明显少了很多。
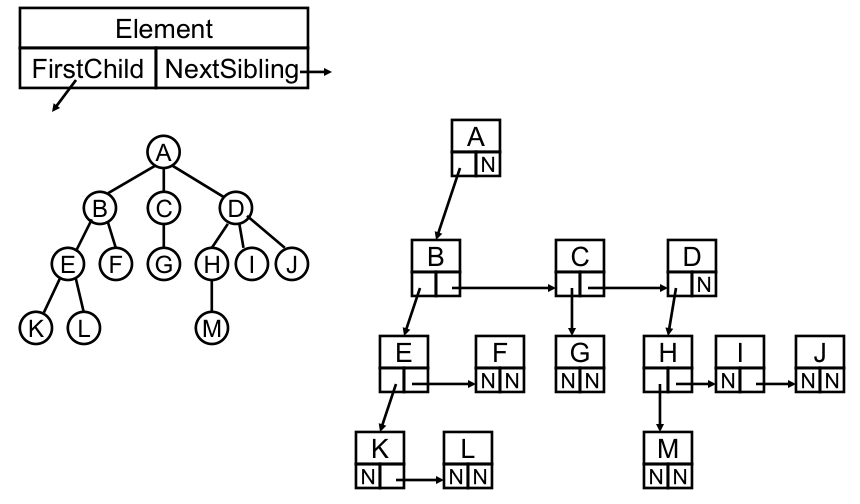
将这种结构旋转45度,其实就是一种二叉树的表示。
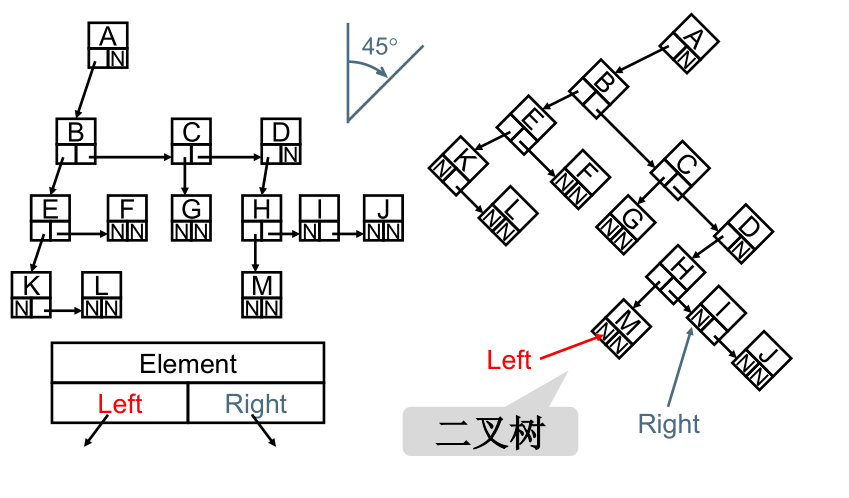
二、二叉树
二叉树(英语:Binary tree)是每个节点最多只有两个分支(不存在分支度大于2的节点)的树结构。通常分支被称作“左子树”和“右子树”。二叉树的分支具有左右次序,不能颠倒。
- 二叉树的定义:
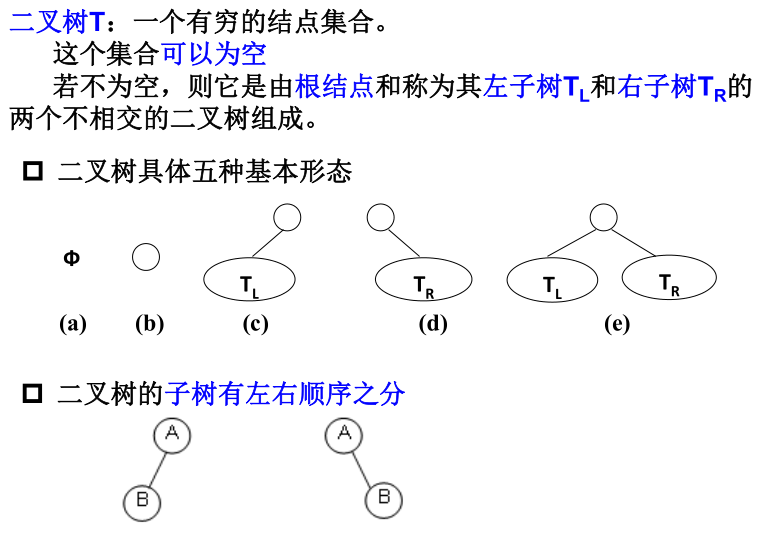
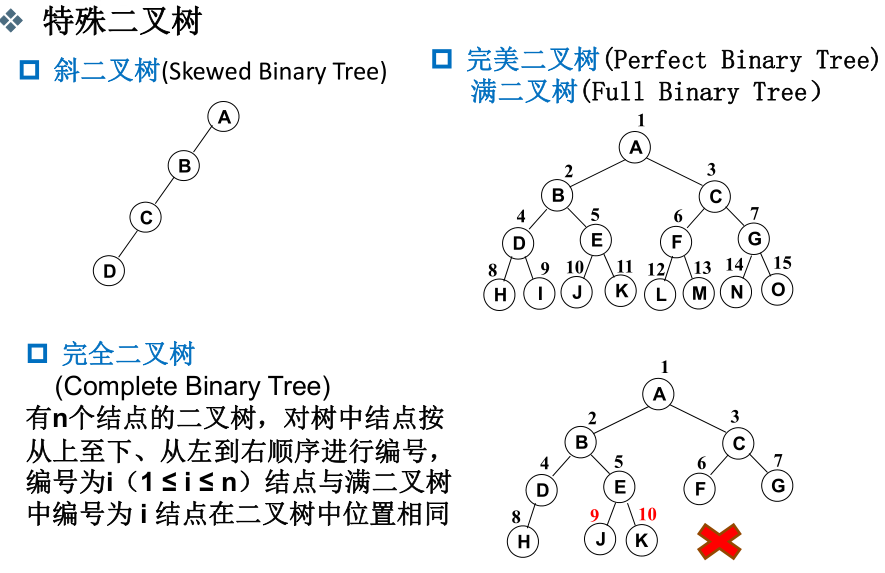
- 二叉树的重要性质:
- 二叉树的抽象数据类型定义

1)数组表示
对于完全二叉树,可以很方便的放到数组中存储,并且很容易就能得到儿子结点,得到父结点。

对于一般的二叉树,也可以使用这种方法存储,但是会造成空间的浪费。
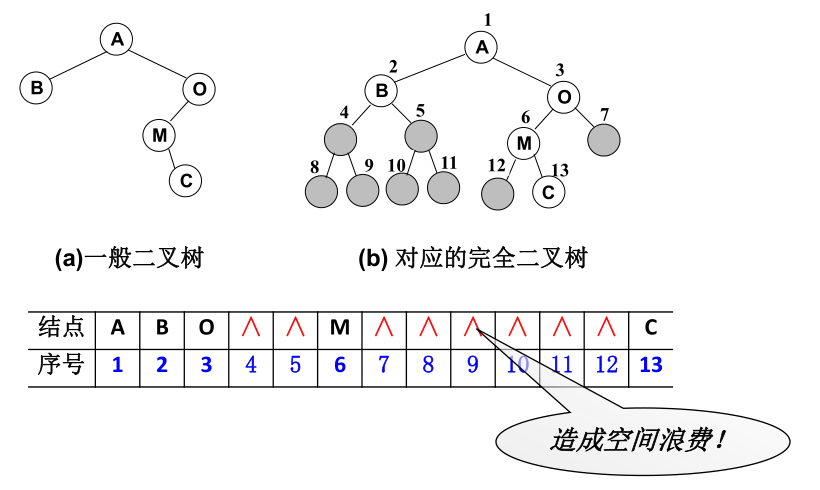
2)链表存储
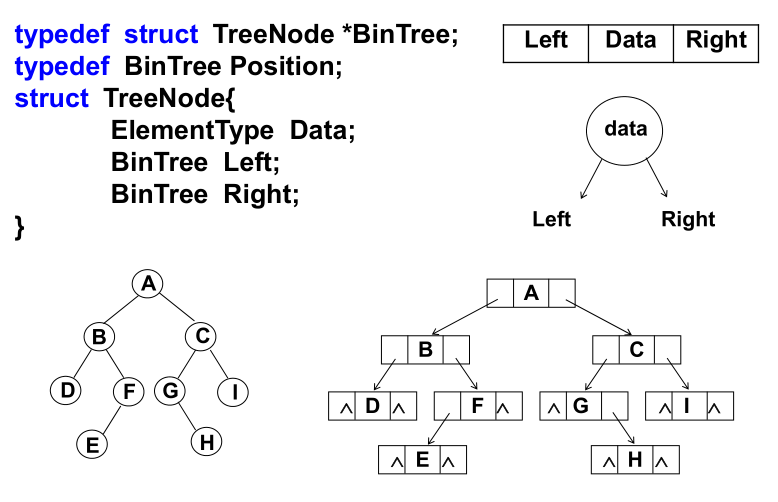
三、二叉树的遍历的递归实现
- 先序遍历

- 中序遍历
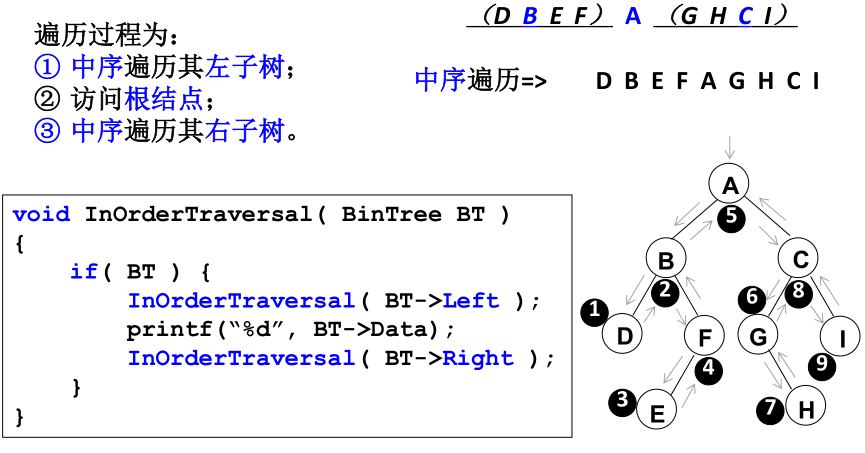
- 后序遍历

三种递归方式的总结:
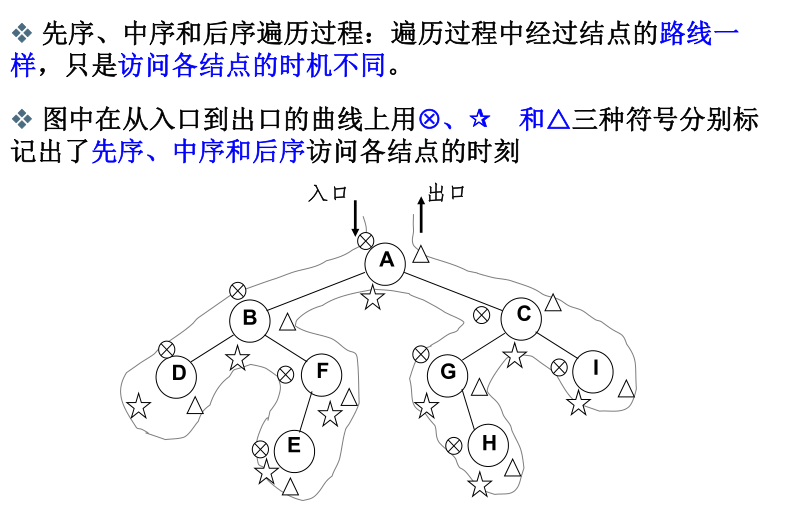
四、二叉树遍历的非递归实现
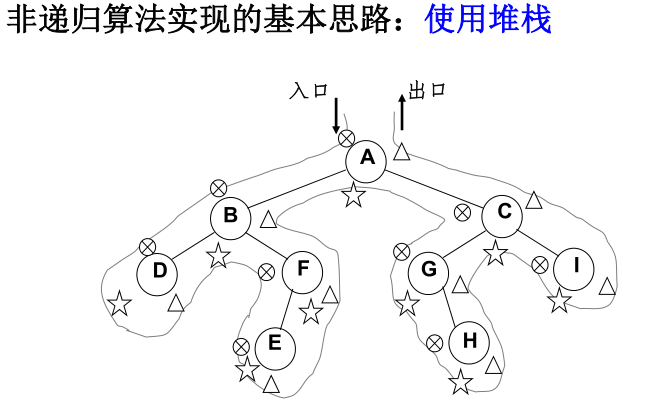
- 中序遍历的非递归实现
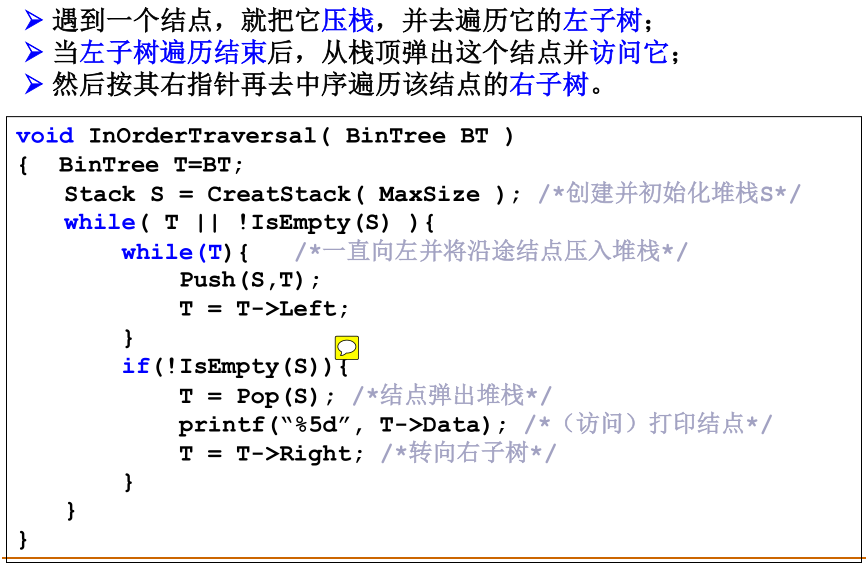
- 先序遍历的非递归实现
第一次压栈其实就是第一次碰到,所以直接在这里输出就可以实现先序遍历。

- 后序遍历的非递归实现
方法一、先序的访问顺序是root, left, right 假设将先序左右对调,则顺序变成root, right, left,暂定称之为“反序”。
后序遍历的访问顺序为left, right,root ,刚好是“反序”结果的逆向输出。于是方法如下:
1、反序遍历二叉树,具体方法为:将先序遍历代码中的left 和right 对调即可。
数据存在堆栈S中。
2、在先序遍历过程中,每次Push节点后紧接着print结点。
对应的,在反序遍历时,将print结点改为把当前结点 PUSH到堆栈Q中。
3、反序遍历完成后,堆栈Q的压栈顺序即为反序遍历的输出结果。
此时再将堆栈Q中的结果pop并print,即为“反序”结果的逆向,也就是后序遍历的结果。
缺点是堆栈Q的深度等于数的结点数,空间占用较大。
void PostOrderTraversal( BinTree BT )
{
BinTree T BT;
Stack S = CreatStack( MaxSize ); /*创建并初始化堆栈S*/
Stack Q = CreatStack( MaxSize ); /*创建并初始化堆栈Q,用于输出反向*/
while( T || !IsEmpty(S) ){
while(T){ /*一直向右并将沿途结点压入堆栈*/
Push(S,T);
Push(Q,T);/*将遍历到的结点压栈,用于反向*/
T = T->Right;
}
if(!IsEmpty(S)){
T = Pop(S); /*结点弹出堆栈*/
T = T->Left; /*转向左子树*/
}
}
while( !IsEmpty(Q) ){
T = Pop(Q);
printf(“%5d”, T->Data); /*(访问)打印结点*/
}
}
方法二、当然也可以使用一个栈进行实现:对于任一结点P,将其入栈,然后沿其左子树一直往下搜索,直到搜索到没有左孩子的结点,此时该结点出现在栈顶,但是此时不能将其出栈并访问,因此其右孩子还为被访问。所以接下来按照相同的规则对其右子树进行相同的处理,当访问完其右孩子时,该结点又出现在栈顶,此时可以将其出栈并访问。这样就保证了正确的访问顺序。可以看出,在这个过程中,每个结点都三次出现在栈顶,只有在第三次出现在栈顶时,才能访问它。因此需要多设置一个变量标识。
void postOrder(BinTree *root) //非递归后序遍历
{
stack<BTNode*> s;
BinTree *p=root;
BTNode *temp;
while(p!=NULL||!s.empty())
{
while(p!=NULL) //沿左子树一直往下搜索,直至出现没有左子树的结点
{
BTNode *btn=(BTNode *)malloc(sizeof(BTNode));
btn->btnode=p;
btn->isFirst=true;
s.push(btn);
p=p->lchild;
}
if(!s.empty())
{
temp=s.top();
s.pop();
if(temp->isFirst==true) //表示是第二次出现在栈顶
{
temp->isFirst=false;
s.push(temp);
p=temp->btnode->rchild;
}
else //第三次出现在栈顶
{
cout<<temp->btnode->data<<" ";
p=NULL;
}
}
}
}
方法三、前面的两种方法都需要额外使用空间,那么是否可以不额外使用更多的空间呢?答案是肯定的。后序遍历的本质就是先遍历左边的,再遍历右的,最后再遍历中间。那么我们只需要在输出中间的数值之前先把他的左右结点压栈就可以了,当然在将其左右子树压栈的时候需要进行判断,具体的判断方式是,定义两个指针,一个指向当前栈顶元素,一个指向上一个出栈元素,不妨设第一个为cur,第二个为pre。能够打印当前的结点的条件是要么其左右子树为空,要么其左右子树都打印完毕。
每次令cur等于当前栈顶的元素,但是不从栈顶弹出,此时分为三种情况:
1)如果cur的左孩子不为空,并且pre不等于cur的左孩子,也不等于其右孩子,说明cur的左孩子还没有打印过,将之压栈;
2)如果上面的条件不满足,表明cur的左孩子已经打印完毕,现在考虑其右孩子。如果cur的右孩子不为空,并且pre不等于cur的右孩子,那么说明cur的右孩子还没有打印,将之压栈。
3)如果上面两个都不满足,说明左右孩子都打印完毕,那么将当前栈顶元素打印,并将pre置为当前打印的结点,弹出栈顶元素。
void postOrder(Node root) {
if (root == null) {
return;
}
else {
Node cur = null;
Node pre = null;
Stack<Node> s = new Stack<>();
s.push(root);
while (!s.empty()) {
cur = s.peek();
if (cur.left != null && pre != cur.left && pre != cur.right)
s.push(cur.left);
else if (cur.right != null && pre != cur.right) {
s.push(cur.right);
}
else {
System.out.println(cur.data);
pre = cur;
s.pop();
}
}
}
}
- 层次遍历
上面谈到的前序,中序,后序遍历本质上都是一种深度优先遍历,显然,也可以使用广度优先进行遍历。也就是层次遍历。

五、二叉树遍历的几个应用
1、求叶结点
很简单,在遍历输出的加上判断就好。
void PreOrderPrintLeaves( BinTree BT )
{
if( BT ) {
if ( !BT-Left && !BT->Right )
printf(“%d”, BT->Data );
PreOrderPrintLeaves ( BT->Left );
PreOrderPrintLeaves ( BT->Right );
}
}
2、求树高度
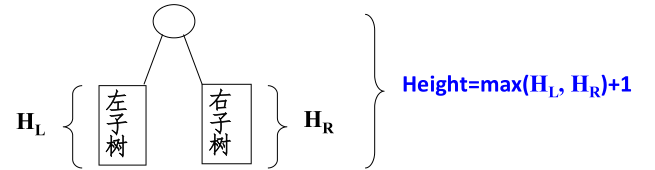
int PostOrderGetHeight( BinTree BT )
{ int HL, HR, MaxH;
if( BT ) {
HL = PostOrderGetHeight(BT->Left); /* 求左子树的深度*/
HR = PostOrderGetHeight(BT->Right); /* 求右子树的深度*/
MaxH = (HL > HR )? HL : HR; /* 取左右子树较大的深度*/
return ( MaxH + 1 ); /* 返回树的深度*/
}
else return 0; /* 空树深度为0 */
}
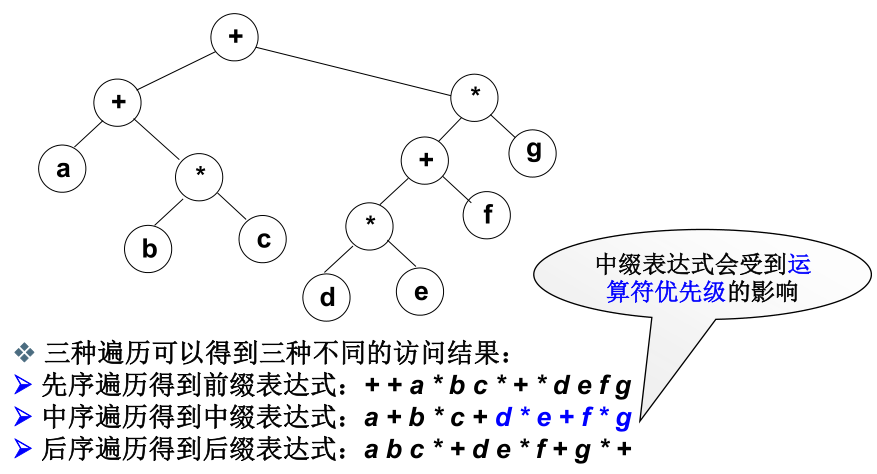
3、二元运算的表达式树
表达式树:叶结点表示运算数,中间结点是运算符。这样通过三种遍历就会得到三种表达式,这其中中缀表达式可能会受运算优先级影响导致不准确(可通过添加括号的方式予以解决)。
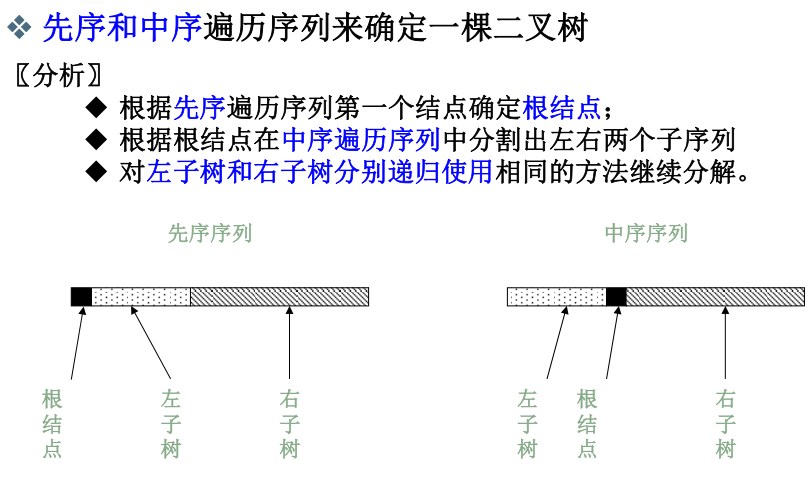
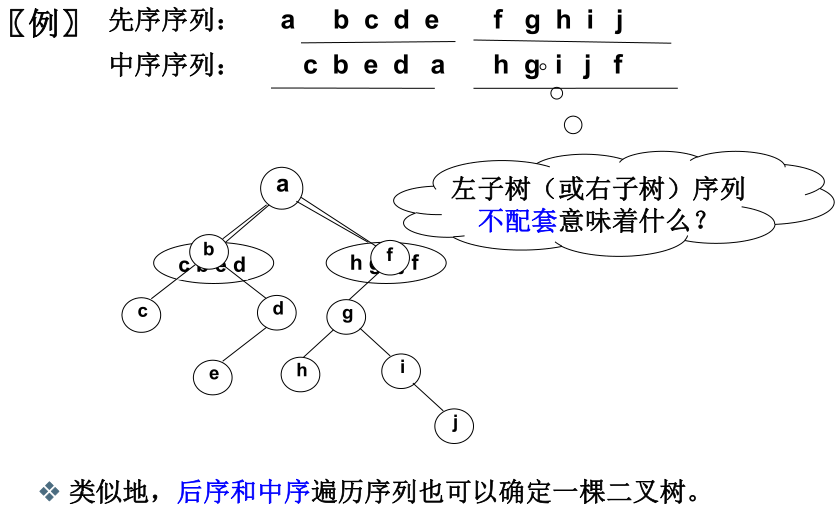
4、两种遍历来构建二叉树
结论是:必须要有中序遍历的结果,才能唯一确定。

因为前序是root,left,right;后序是left,right,root。根是容易确定的,一个在最前面,一个在最后面,但是左右子树可能会发生混淆。
举例使用前序,中序构建二叉树: