二叉搜索树BST

二叉搜索树（英语：Binary Search Tree），也称二叉查找树、有序二叉树（英语：ordered binary tree），排序二叉树（英语：sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

1. 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
2. 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
3. 任意节点的左、右子树也分别为二叉查找树；
4. 没有键值相等的节点。

中序遍历二叉查找树可得到一个关键字的有序序列，一个无序序列可以通过构造一棵二叉查找树变成一个有序序列，构造树的过程即为对无序序列进行查找的过程。每次插入的新的结点都是二叉查找树上新的叶子结点，在进行插入操作时，不必移动其它结点，只需改动某个结点的指针，由空变为非空即可。

一、查找问题

查找问题是一个非常基础的问题，查找本身也是一个非常常用的操作。

查找分为动态查找和静态查找。

所谓静态查找就是数据不再发生变化，换句话说，就是没有insert，delete操作，针对这种查找类型，我们可以使用二分查找法。

二分查找算法步骤：

// 递归版本
int binary_search(const int arr[], int start, int end, int khey) {
	if (start > end)
		return -1;

	int mid = start + (end - start) / 2;    //直接平均可能會溢位，所以用此算法
	if (arr[mid] > khey)
		return binary_search(arr, start, mid - 1, khey);
	else if (arr[mid] < khey)
		return binary_search(arr, mid + 1, end, khey);
	else
	    return mid;        //最後檢測相等是因為多數搜尋狀況不是大於要不就小於
}

 

// while循环
int binary_search(const int arr[], int start, int end, int khey) {
    int ret = -1;       // 未搜索到数据返回-1下标
    
	int mid;
	while (start <= end) {
		mid = start + (end - start) / 2; //直接平均可能會溢位，所以用此算法
		if (arr[mid] < khey)
			start = mid + 1;
		else if (arr[mid] > khey)
			end = mid - 1;
		else {            // 最後檢測相等是因為多數搜尋狀況不是大於要不就小於
			ret = mid;  
            break;
        }
	}
	
	return ret;     // 单一出口
}

二分查找算法有一个前提就是数组是一个有序数组，在保证数组有序的前提下才能使用这种算法。那如果此时要向数组中增加和删除元素最坏的时间复杂度是O（n），另外，如果原数组不是有序的，那么还需要首先对数组进行排序，这样又会增加O（nlogn）的开销。

那么为什么不直接把数据存储成为类似二分搜索的形式呢？于是二叉搜索树就“闪亮登场”了。

 

二、二叉搜索树

针对动态查找，二叉查找树可以在期望O（logn）的时间复杂度(最坏情况下也是O（n）：数列有序，树退化成线性表)内完成find，insert，delete操作。

虽然二叉查找树的最坏效率是O(n),但它支持动态查询，且有很多改进版的二叉查找树可以使树高为logn，,如SBT,AVL树，红黑树等。故不失为一种好的动态查找方法。

O ( log ⁡ n ) {\displaystyle O(\log n)} ,如SBT,AVL树，红黑树等。故不失为一种好的动态查找方法。

• 二叉搜索树的查找操作：Find

Position Find( ElementType X, BinTree BST )
{
    if( !BST ) return NULL; /* 查找失败*/
    if( X > BST->Data )
        return Find( X, BST->Right ); /* 在右子树中继续查找*/
    Else if( X < BST->Data )
        return Find( X, BST->Left ); /* 在左子树中继续查找*/
    else /* X == BST->Data */
        return BST; /* 查找成功 ， 返回结点的找到结点的地址*/
}    

由于非递归函数执行效率高，并且不会出现递归层数过多导致的栈溢出的情况，所以可以使用循环操作来取代递归。

Position IterFind( ElementType X, BinTree BST )
{
    while( BST ) {
    if( X > BST->Data )
        BST = BST->Right; /* 向右子树中移动 ， 继续查找*/
    else if( X < BST->Data )
        BST = BST->Left; /* 向左子树中移动 ， 继续查找*/
    else /* X == BST->Data */
        return BST; /* 查找成功 ， 返回结点的找到结点的地址*/
    }
    return NULL; /* 查找失败*/
}

查找的效率决定于树的高度，所以之后出现了平衡二叉树来解决这个问题。

查找最大和最小元素：

1）最大元素 一定是在树的 最右分枝的端结点上

2）最小元素 一定是在树的 最左分枝的端结点上

查找最小元素的 递归 函数：

Position FindMin( BinTree BST )
{
    if( !BST ) return NULL; /* 空的二叉搜索树，返回NULL*/
    else if( !BST->Left )
        return BST; /* 找到最左叶结点并返回*/
    else
        return FindMin( BST->Left ); /* 沿左分支继续查找*/
}        

查找最大元素的 迭代 函数：

Position FindMax( BinTree BST )
{
    if(BST )
    while( BST->Right ) BST = BST->Right;
    /* 沿右分支继续查找，直到最右叶结点*/
    return BST;
}

• 二叉搜索树的插入：Insert

关键是要找到元素应该插入的位置， 可以采用与Find类似的方法。

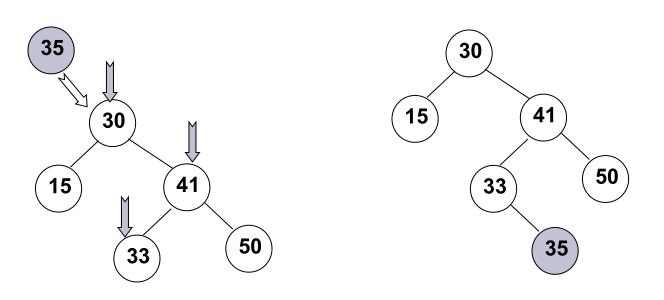
BinTree Insert( ElementType X, BinTree BST )
{
    if( !BST ){
        /* 若原树为空 ， 生成并返回一个结点的二叉搜索树*/
        BST = malloc(sizeof(struct TreeNode));
        BST->Data = X;
        BST->Left = BST->Right = NULL;
    }else{ /* 开始找要插入元素的位置*/
        if( X < BST->Data )
             /* 递归插入左子树*/
            BST->Left = Insert( X, BST->Left);
        else if( X > BST->Data )
             /* 递归插入右子树*/
            BST->Right = Insert( X, BST->Right);
        /* else X 已经存在 ， 什么都不做 */
    }
    return BST;
}            

• 二叉搜索树的删除：Delete

考虑三种情况：

1）要删除的是叶结点 ： 直接删除，并再修改其父结点指针--- 置为NULL

 

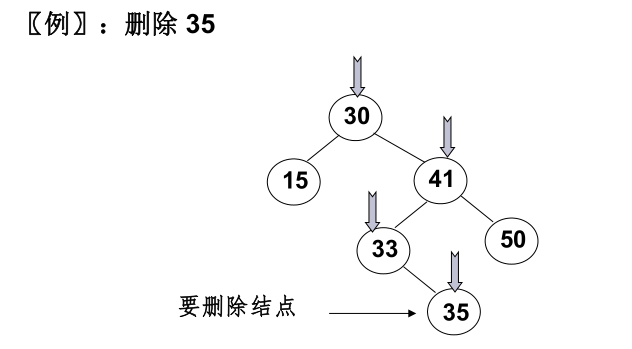
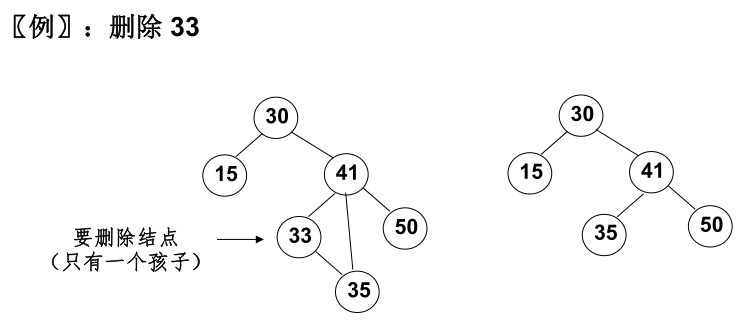
2）要删除的结点 只有一个孩子点 结点：将其 父结点 的指针指向要删除结点的孩子结点

3）要删除的结点 有左右两个子树：用另一结点替代被删除结点：右子树的最小元素 或者 左子树的最大元素。

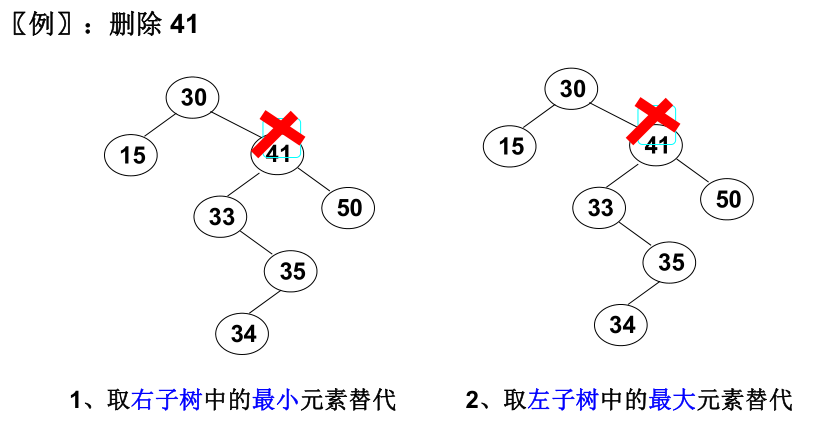
这种方法的好处是，右子树的最小元素必不可能有两个孩子，左子树中的最大元素也必不可能有两个孩子，也就是将复杂情况转化成了简单情况。

BinTree Delete(ElementType X, BinTree BST) {
    Position Tmp;
    if (!BST) printf(" 要删除的元素未找到");
    else if (X < BST -> Data)
        BST -> Left = Delete(X, BST -> Left); /*  左子树递归删除 */
    else if (X > BST -> Data)
        BST -> Right = Delete(X, BST -> Right); /*  右子树递归删除 */
    else /* 找到要删除的结点 */
        if (BST -> Left && BST -> Right) { /* 被删除结点有左右两个子结点 */
            Tmp = FindMin(BST -> Right);
            /* 在右子树中找最小的元素填充删除结点*/
            BST -> Data = Tmp -> Data;
            /* 在删除结点的右子树中删除最小元素*/
            BST -> Right = Delete(BST -> Data, BST -> Right);
        } else { /* 被删除结点有一个或无子结点*/
            Tmp = BST;
            if (!BST -> Left) /*  有右孩子或无子结点*/
                BST = BST -> Right;
            else if (!BST -> Right) /* 有左孩子或无子结点*/
                BST = BST -> Left;
            free(Tmp);
        }
    return BST;
}