遗传算法 Genetic Algorithm
2017-12-17 19:12:10
一、Evolutionary Algorithm
进化算法,也被成为是演化算法(evolutionary algorithms,简称EAs),它不是一个具体的算法,而是一个“算法簇”。进化算法的产生的灵感借鉴了大自然中生物的进化操作,它一般包括基因编码,种群初始化,交叉变异算子,经营保留机制等基本操作。与传统的基于微积分的方法和穷举方法等优化算法相比,进化计算是一种成熟的具有高鲁棒性和广泛适用性的全局优化方法,具有自组织、自适应、自学习的特性,能够不受问题性质的限制,有效地处理传统优化算法难以解决的复杂问题(比如NP难优化问题)。
除了上述优点以外,进化算法还经常被用到多目标问题的优化求解中来,我们一般称这类进化算法为进化多目标优化算法(MOEAs)。目前进化计算的相关算法已经被广泛用于参数优化、工业调度、资源分配、复杂网络分析等领域。
二、Genetic Algorithm
遗传算法(Genetic Algorithm,简称GA)是一种最基本的进化算法,它是模拟达尔文生物进化理论的一种优化模型,最早由J.Holland教授于1975年提出。遗传算法中种群分每个个体都是解空间上的一个可行解,通过模拟生物的进化过程,从而在解空间内搜索最优解。
遗传算法的基本操作可以用下图来描述:
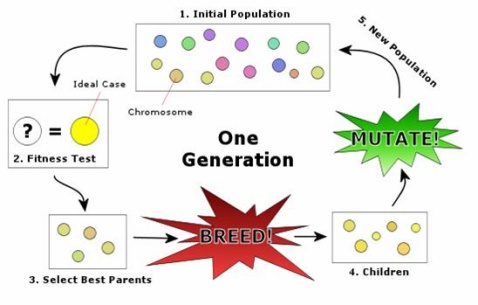
个体的编码方式确定以后,针对上图操作的具体描述如下:
Step 1 种群初始化:根据问题特性设计合适的初始化操作(初始化操作应尽量简单,时间复杂度不易过高)对种群中的N个个体进行初始化操作;
Step 2 个体评价:根据优化的目标函数计算种群中个体的适应值(fitness value);
Step 3 迭代设置:设置种群最大迭代次数gmax,并令当前迭代次数g=1;
Step 4 个体选择:设计合适的选择算子来对种群P(g)个体进行选择,被选择的个体将进入交配池中组成父代种群FP(g),用于交叉变换以产生新的个体。选择策略要基于个体适应值来进行,假如要优化的问题为最小化问题,那么具有较小适应值的个体被选择的概率相应应该大一些。常用的选择策略有轮盘赌选择,锦标赛选择等。
Step 5 交叉算子:根据交叉概率pm(预先指定,一般为0.8)来判断父代个体是否需要进行交叉操作。交叉算子要根据被优化问题的特性来设计,它是整个遗传算法的核心,它被设计的好坏将直接决定整个算法性能的优劣。
Step 6 变异算子:根据变异概率pc(预先指定,一般为0.1)来判断父代个体是否需要进行变异操作。变异算子的主要作用是保持种群的多样性,防止种群陷入局部最优,所以其一般被设计为一种随机变换。
通过交叉变异操作以后父代种群FP(g)生成了新的子代种群P(g+1),令种群迭代次数g=g+1,进行下一轮的迭代操作(跳转到Step 4),直至迭代次数达到最大的迭代次数。
需要注意的问题:
1)种群数目
太多会导致收敛很慢,太少会落入局部最优值。需要不断尝试得到一个合适的种群数目。
2)交叉繁殖概率
一般建议设置为0.8。
3)变异概率
建议值为1/Population,如果种群值为100,则建议为0.01。太大会破坏整个算法的正确执行,太小会导致种群的多样性下降,会导致陷入局部最优。
4)挑选方式
- 轮盘赌
一是最原始的轮盘竞赛方式,也就是适应度高的在轮盘上的比例就高,比例值和其自身的比例值相对应。
有个问题就是,如果出现负值就没法处理。可以改进一下,轮盘中的比例是固定的,只和排名有关。
- 精英选择(TOP-K)
举个例子:
求解函数 f(x) = x + 10*sin(5*x) + 7*cos(4*x) 在区间[0,9]的最大值。
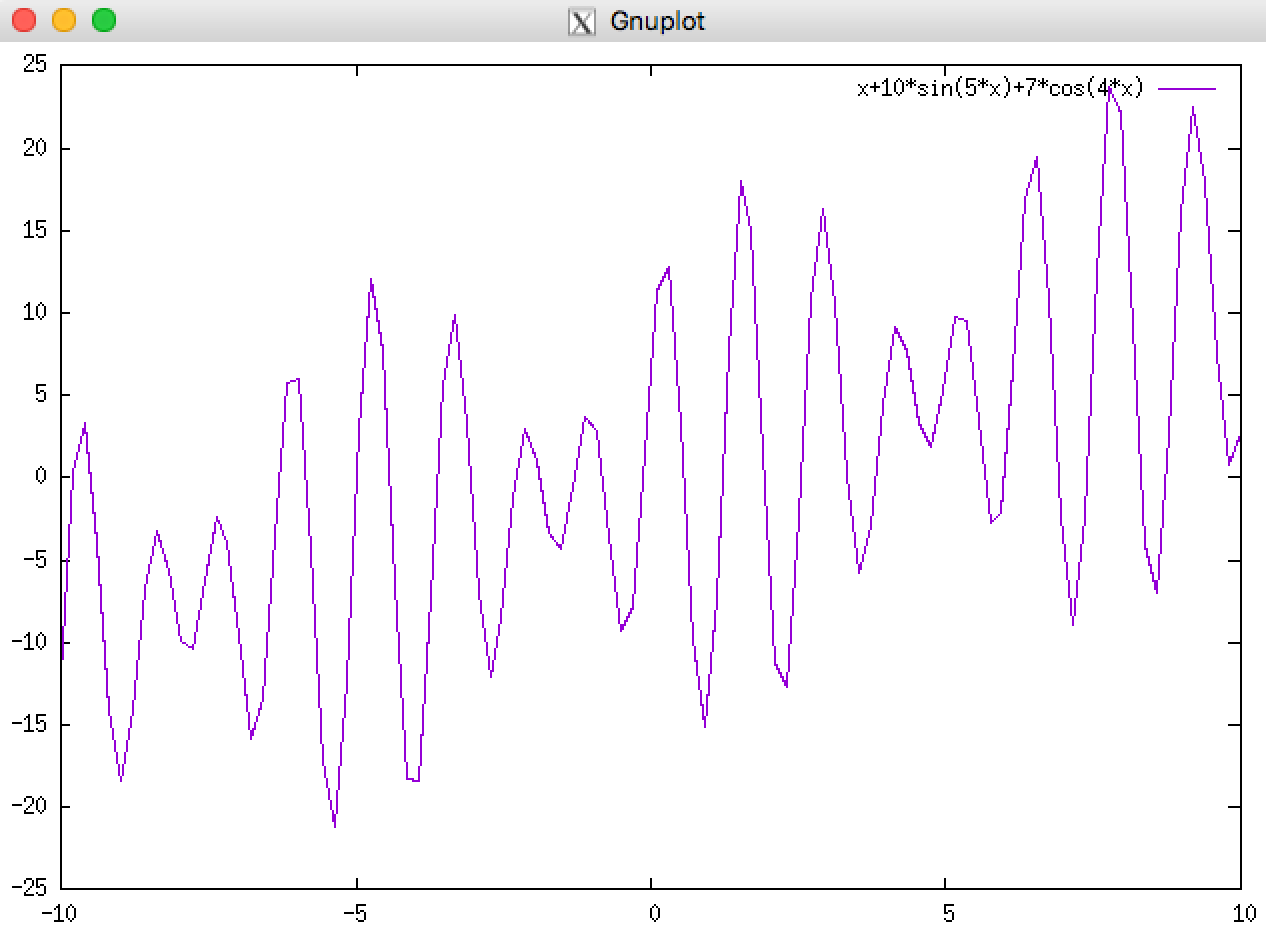
事实上,不管一个函数的形状多么奇怪,遗传算法都能在很短的时间内找到它在一个区间内的(近似)最大值。
1.编码
实现遗传算法的第一步就是明确对求解问题的编码和解码方式。
对于函数优化问题,一般有两种编码方式,各具优缺点
- 实数编码:直接用实数表示基因,容易理解且不需要解码过程,但容易过早收敛,从而陷入局部最优
- 二进制编码:稳定性高,种群多样性大,但需要的存储空间大,需要解码且难以理解
一开始,这些二进制串是随机生成的。一个这样的二进制串代表一条染色体串,这里染色体串的长度为17。对于任何一条这样的染色体chromosome,如何将它复原(解码)到[0,9]这个区间中的数值呢?
对于本问题,我们可以采用以下公式来解码:
x = 0 + decimal(chromosome)×(9-0)/(2^17-1)
更一般的公式为:
f(x), x∈[lower_bound, upper_bound] x = lower_bound + decimal(chromosome)×(upper_bound-lower_bound)/(2^chromosome_size-1)
lower_bound: 函数定义域的下限
upper_bound: 函数定义域的上限
chromosome_size: 染色体的长度
2.个体和种群
『染色体』表达了某种特征,这种特征的载体,称为『个体』。
对于本次实验所要解决的一元函数最大值求解问题,个体可以用上一节构造的染色体表示,一个个体里有一条染色体。
许多这样的个体组成了一个种群,其含义是一个一维点集(x轴上[0,9]的线段)。
3.适应度函数
遗传算法中,一个个体(解)的好坏用适应度函数值来评价,在本问题中,f(x)就是适应度函数。
适应度函数值越大,解的质量越高。
适应度函数是遗传算法进化的驱动力,也是进行自然选择的唯一标准,它的设计应结合求解问题本身的要求而定。
4.遗传算子
我们希望有这样一个种群,它所包含的个体所对应的函数值都很接近于f(x)在[0,9]上的最大值,但是这个种群一开始可能不那么优秀,因为个体的染色体串是随机生成的。
如何让种群变得优秀呢?
不断的进化。
每一次进化都尽可能保留种群中的优秀个体,淘汰掉不理想的个体,并且在优秀个体之间进行染色体交叉,有些个体还可能出现变异。
种群的每一次进化,都会产生一个最优个体。种群所有世代的最优个体,可能就是函数f(x)最大值对应的定义域中的点。
如果种群无休止地进化,那总能找到最好的解。但实际上,我们的时间有限,通常在得到一个看上去不错的解时,便终止了进化。
对于给定的种群,如何赋予它进化的能力呢?
- 首先是选择(selection)
- 选择操作是从前代种群中选择***多对***较优个体,一对较优个体称之为一对父母,让父母们将它们的基因传递到下一代,直到下一代个体数量达到种群数量上限
- 在选择操作前,将种群中个体按照适应度从小到大进行排列
- 采用轮盘赌选择方法(当然还有很多别的选择方法),各个个体被选中的概率与其适应度函数值大小成正比
- 轮盘赌选择方法具有随机性,在选择的过程中可能会丢掉较好的个体,所以可以使用精英机制,将前代最优个体直接选择
- 其次是交叉(crossover)
- 两个待交叉的不同的染色体(父母)根据交叉概率(cross_rate)按某种方式交换其部分基因
- 采用单点交叉法,也可以使用其他交叉方法
- 最后是变异(mutation)
- 染色体按照变异概率(mutate_rate)进行染色体的变异
- 采用单点变异法,也可以使用其他变异方法
#encoding=utf-8
import math
import random
import operator
class GA():
def __init__(self, length, count):
# 染色体长度
self.length = length
# 种群中的染色体数量
self.count = count
# 随机生成初始种群
self.population = self.gen_population(length, count)
def evolve(self, retain_rate=0.2, random_select_rate=0.5, mutation_rate=0.01):
"""
进化
对当前一代种群依次进行选择、交叉并生成新一代种群,然后对新一代种群进行变异
"""
parents = self.selection(retain_rate, random_select_rate)
self.crossover(parents)
self.mutation(mutation_rate)
def gen_chromosome(self, length):
"""
随机生成长度为length的染色体,每个基因的取值是0或1
这里用一个bit表示一个基因
"""
chromosome = 0
for i in xrange(length):
chromosome |= (1 << i) * random.randint(0, 1)
return chromosome
def gen_population(self, length, count):
"""
获取初始种群(一个含有count个长度为length的染色体的列表)
"""
return [self.gen_chromosome(length) for i in xrange(count)]
def fitness(self, chromosome):
"""
计算适应度,将染色体解码为0~9之间数字,代入函数计算
因为是求最大值,所以数值越大,适应度越高
"""
x = self.decode(chromosome)
return x + 10*math.sin(5*x) + 7*math.cos(4*x)
def selection(self, retain_rate, random_select_rate):
"""
选择
先对适应度从大到小排序,选出存活的染色体
再进行随机选择,选出适应度虽然小,但是幸存下来的个体
"""
# 对适应度从大到小进行排序
graded = [(self.fitness(chromosome), chromosome) for chromosome in self.population]
graded = [x[1] for x in sorted(graded, reverse=True)]
# 选出适应性强的染色体
retain_length = int(len(graded) * retain_rate)
parents = graded[:retain_length]
# 选出适应性不强,但是幸存的染色体
for chromosome in graded[retain_length:]:
if random.random() < random_select_rate:
parents.append(chromosome)
return parents
def crossover(self, parents):
"""
染色体的交叉、繁殖,生成新一代的种群
"""
# 新出生的孩子,最终会被加入存活下来的父母之中,形成新一代的种群。
children = []
# 需要繁殖的孩子的量
target_count = len(self.population) - len(parents)
# 开始根据需要的量进行繁殖
while len(children) < target_count:
male = random.randint(0, len(parents)-1)
female = random.randint(0, len(parents)-1)
if male != female:
# 随机选取交叉点
cross_pos = random.randint(0, self.length)
# 生成掩码,方便位操作
mask = 0
for i in xrange(cross_pos):
mask |= (1 << i)
male = parents[male]
female = parents[female]
# 孩子将获得父亲在交叉点前的基因和母亲在交叉点后(包括交叉点)的基因
child = ((male & mask) | (female & ~mask)) & ((1 << self.length) - 1)
children.append(child)
# 经过繁殖后,孩子和父母的数量与原始种群数量相等,在这里可以更新种群。
self.population = parents + children
def mutation(self, rate):
"""
变异
对种群中的所有个体,随机改变某个个体中的某个基因
"""
for i in xrange(len(self.population)):
if random.random() < rate:
j = random.randint(0, self.length-1)
self.population[i] ^= 1 << j
def decode(self, chromosome):
"""
解码染色体,将二进制转化为属于[0, 9]的实数
"""
return chromosome * 9.0 / (2**self.length-1)
def result(self):
"""
获得当前代的最优值,这里取的是函数取最大值时x的值。
"""
graded = [(self.fitness(chromosome), chromosome) for chromosome in self.population]
graded = [x[1] for x in sorted(graded, reverse=True)]
return ga.decode(graded[0])
if __name__ == '__main__':
# 染色体长度为17, 种群数量为300
ga = GA(17, 300)
# 200次进化迭代
for x in xrange(200):
ga.evolve()
print ga.result()
三、Genetic Programming
遗传编程或称基因编程,简称GP,是一种从生物演化过程得到灵感的自动化生成和选择计算机程序来完成用户定义的任务的技术。从理论上讲,人类用遗传编程只需要告诉计算机“需要完成什么”,而不用告诉它“如何去完成”,最终可能实现真正意义上的人工智能:自动化的发明机器。
GP的输出是一个程序,可以用来控制机器人,进行函数回归等。
GP中有两个重要的概念:
1)Terminal Set,包含变量和常量等;
2)Function Set,主要是一些函数,可以是加减乘除,也可以是一些复杂的函数;
GP里进化的实际上是一颗树,如图。
1.Crossover杂交(允许自杂交)
2.Mutation变异
举个例子:
使用GP进行回归,具体来说是生成一些点,之后使用GP来训练得到符合这些点的函数。适应度定义为差值的总和。






