推荐算法
2017-12-04 15:20:07
所谓推荐算法就是利用用户的一些行为,通过一些数学算法,推测出用户可能喜欢的东西。
推荐算法主要有两种:
- 基于内容:
- 协同过滤:
idf:Inverse Document Frequency,也就是单词在所有文档中的出现频率的倒数的log。
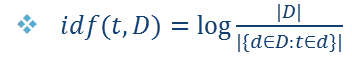
TF-idf:
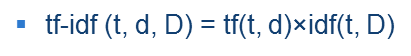
所以我们认为一个单词为一篇文档的频繁词要满足两个条件,一是该搜索词在该片中反复出现,二是在其他文档中出现的比较少。
对于一句话那就是多个tf-idf值的加和。
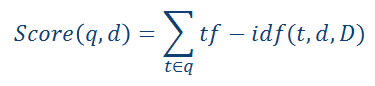
向量空间模型:
计算机是无法识别一个文档的,但是我们可以给出一组关键词,用这组关键词来表示这个文档。
这里的W值可以是0,1表示该关键词有没有出现,也可以是计数值,也可以上TF-idf值。
有了向量空间模型之后,我们可以通过向量求余弦值来对两篇文章的关联度进行分析:
Cosine Similarity:
显然,cosine值为1则最为相关,如果为0则最不相关。那么就可以通过这种方法来进行文本聚类,或者进行语句与文本的关联度分析。
这种方法有两个问题:
- 同一含义多种单词,比如搜car,其实vehicle,Automobile等都是表示同样的含义,但是在使用余弦的时候会返回一个很小的值,表示不太相关。
- 同一单词多种含义,比如Apple,可能是指苹果公司,可能是指食物苹果,这样就会导致结果的精准度很差。
解决方法其中之一就是使用奇异值分解的隐含语义分析算法。
隐含语义分析 Latent semantic analysis:
传统向量空间模型使用精确的词匹配,即精确匹配用户输入的词与向量空间中存在的词。由于一词多义(polysemy)和一义多词(synonymy)的存在,使得该模型无法提供给用户语义层面的检索。比如用户搜索”automobile”,即汽车,传统向量空间模型仅仅会返回包含”automobile”单词的页面,而实际上包含”car”单词的页面也可能是用户所需要的。
此时,就可以使用隐含语义分析技术将原单词中的隐含信息提取出来。具体来说采用的技术是奇异值分解技术SVD(singular value decomposition)。
多篇文章的向量空间模型可以组成一个矩阵,不妨用X来表示:
对X的矩阵进行SVD变换:
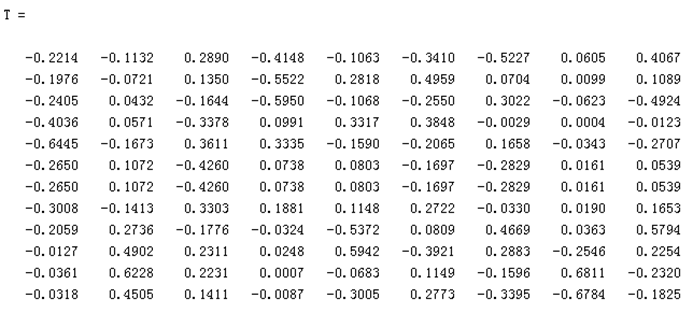


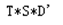

其中的S矩阵的各个量的大小表示隐含属性的比重大小,因此可以进行挑选其中较大的几个属性,将对结果影响不大的进行剔除,这样就可以排除噪声的影响。
这里不妨取两个最大的值,并将精简后的三个矩阵乘起来,可以看到矩阵的变化并不大。
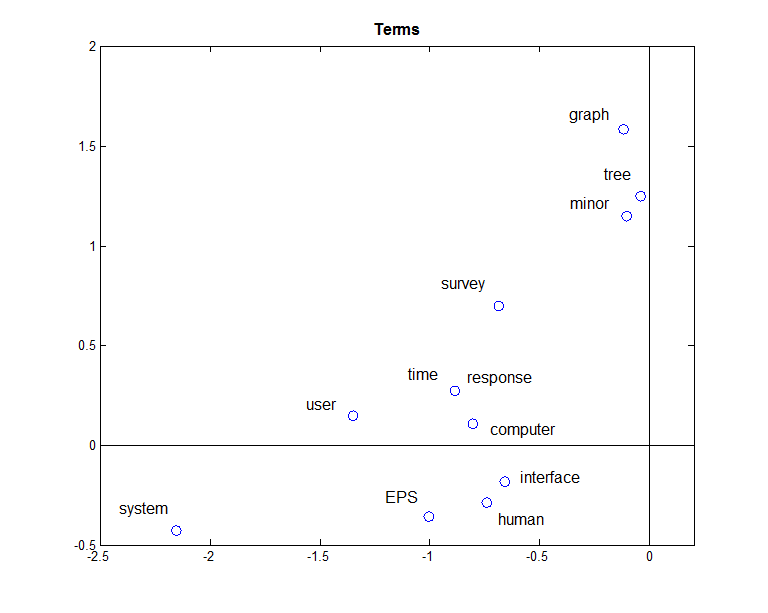
Document的向量表示为DS,将坐标画出来如图:
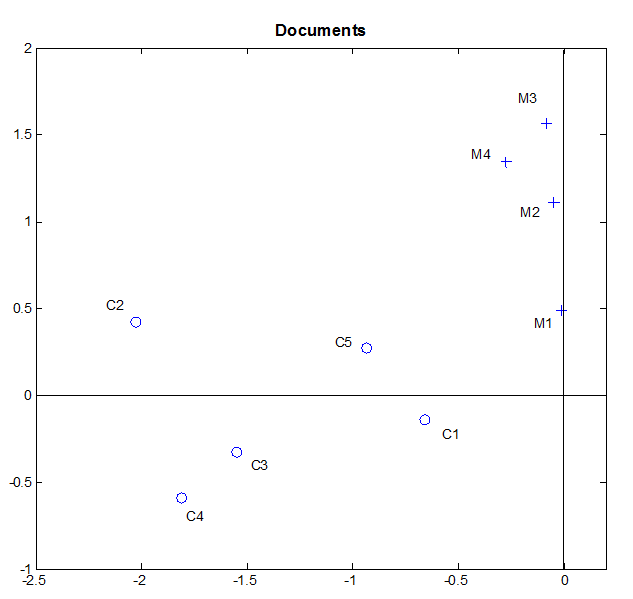
可以看出聚类的效果还是比较好的,再通过求cosine值,就可以更好的进行相似性分析。可以看出,进行了隐含语义分析的矩阵的相似度分析的值更大,也就是表示区分度更大,更容易区分。
对于一篇陌生的文档如何进行区分呢,以下给出了一种解法
- 网页的PageRank值由指向他的网页决定,而非由自身的链接决定,这就一定程度上避免了一个网页为了提高PageRank值而广扩链接;
- 投票的重要性和推荐网页的数目有关,类比于保研教授推荐,如果该教授经常推荐那么其效力就会下降,如果该老师只推荐了很少的同学而你就是其中之一,那么效力就会高很多。
协同过滤是利用集体智慧的一个典型方法。要理解什么是协同过滤 (Collaborative Filtering, 简称 CF),首先想一个简单的问题,如果你现在想看个电影,但你不知道具体看哪部,你会怎么做?大部分的人会问问周围的朋友,看看最近有什么好看的电影推荐,而我们一般更倾向于从口味比较类似的朋友那里得到推荐。这就是协同过滤的核心思想。
协同过滤算法的工作流程:
- 创建打分矩阵
- 通过矩阵得到相似度高的用户群
- 推荐那些各个用户群里打分高的产品
协同过滤主要分为三类:
- 基于用户的协同过滤推荐(User-based Collaborative Filtering Recommendation)
- 基于项目的协同过滤推荐(Item-based Collaborative Filtering Recommendation)
- 基于模型的协同过滤推荐(Model-based Collaborative Filtering Recommendation)
1)基于用户的协同过滤推荐(User-based Collaborative Filtering Recommendation)
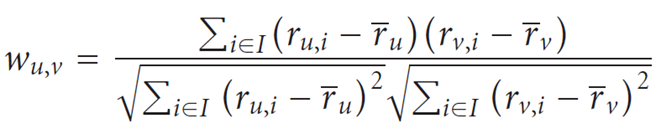
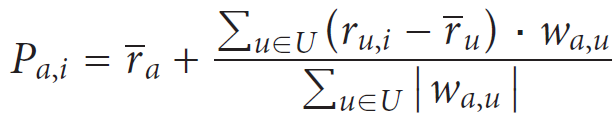
公式一用来计算u,v两个用户的相关系数,相关系数|w|<=1,如果|w|=1,则两者成线性相关。

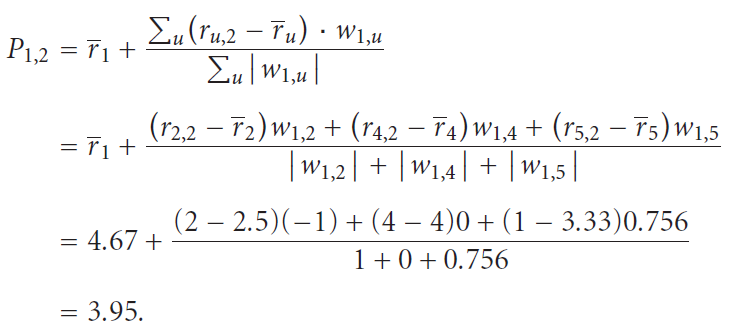
2)基于项目的协同过滤推荐(Item-based Collaborative Filtering Recommendation)
方法一、与User-based CF进行类比,既然基于用户的协同过滤是采用的计算用户之间的相关系数,最后得到未知的item的打分,那么,Item-based CF也可以使用相关系数进行计算。
同样的公式一用于计算i,j两件商品的相关性,
公式二用于计算用户a的对商品i的打分。
当然,也可以不使用这种类比的方式来进行计算,也有其他的更讨巧的方法。
方法二、通过其他用户第i项与平均值的差来估算用户a。





 及
及 的
的
