L1正则化与稀疏性

2020-04-21 22:32:57

问题描述：L1正则化使得模型参数具有稀疏性的原理是什么。

问题求解：

稀疏矩阵指有很多元素为0，少数参数为非零值。一般而言，只有少部分特征对模型有贡献，大部分特征对模型没有贡献或者贡献很小，稀疏参数的引入，使得一些特征对应的参数是0，所以就可以剔除可以将那些没有用的特征，从而实现特征选择，提高模型的泛化能力，降低过拟合的可能。

L1正则化使得参数稀疏可以从函数的角度来看，仅考虑一维的情况，多维情况是类似的，如图所示。假设棕线是原始目标函数L(w)的曲线图，显然最小值点在蓝点处，且对应的w*值非0。

 

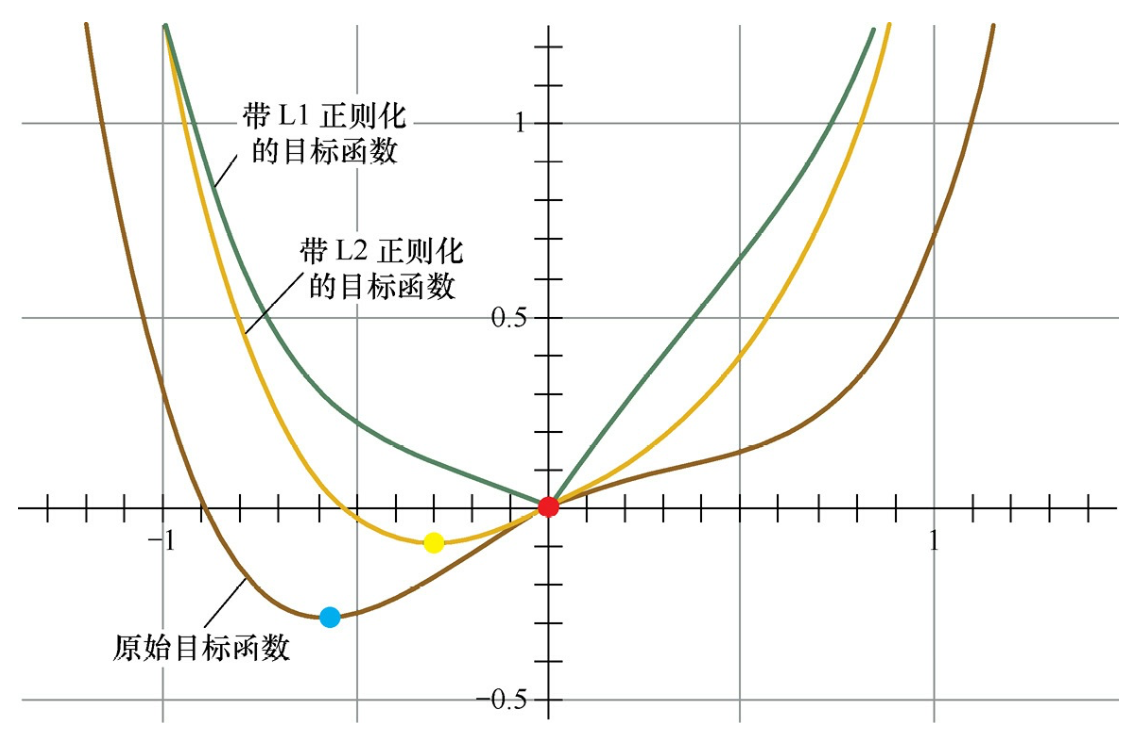
首先，考虑加上L2正则化项，目标函数变成L(w)+Cw2，其函数曲线为黄色。

此时，最小值点在黄点处，对应的w*的绝对值减小了，但仍然非0。 然后，考虑加上L1正则化项，目标函数变成L(w)+C|w|，其函数曲线为绿色。

此时，最小值点在红点处，对应的w是0，产生了稀疏性。

产生上述现象的原因也很直观。加入L1正则项后，对带正则项的目标函数求导，正则项部分产生的导数在原点左边部分是−C，在原点右边部分是C，因此，只要原目标函数的导数绝对值小于C，那么带正则项的目标函数在原点左边部分始 终是递减的，在原点右边部分始终是递增的，最小值点自然在原点处。相反，L2 正则项在原点处的导数是0，只要原目标函数在原点处的导数不为0，那么最小值 点就不会在原点，所以L2只有减小w绝对值的作用，对解空间的稀疏性没有贡献。