图-搜索-DFS-51. N皇后

2020-03-15 19:49:59

问题描述：

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

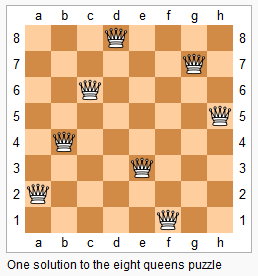
上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例:

输入: 4
输出: [
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],

["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

问题求解：

N皇后问题是非常经典的回溯法问题，其核心思路就是使用回溯法去遍历解空间，并利用条件进行剪枝操作。

这里，我采用的是按行去放置皇后，那么我们就不需要记录行的放置信息了，因为这样可以保证一行内只有一个棋子。

我们还需要col[]数组去记录列的放置信息，diag1[]，diag2[]数组去保存对角线的位置信息。

这里有个地方比较麻烦的就是对角线怎么表示，事实上对于主对角线i - j是一个常数，对于次对角线i + j是个常数。

我们可以很直观的看到次对角线的和是个常数，因为i + 1的时候伴随着j - 1;

对于主对角线，我们可以这样来判断。

第一行次对角线坐标的变化:(0, 0) -> (0, 1) -> (0, 2)...

第一行主对角线坐标的变化:(0, n-1) -> (0, n-2) -> (0, n-3)...

不难发现，只需要使用n - 1 - j就可以将其转化为次对角线的坐标关系。

剩下来就是一行一行的的去放置皇后并检测是否合理了。

时间复杂度：O(n!)

    int[] col;
    int[] diag1;
    int[] diag2;
    List<List<String>> res = new ArrayList<>();
    public List<List<String>> solveNQueens(int n) {
        col = new int[n];
        diag1 = new int[2 * n - 1];
        diag2 = new int[2 * n - 1];
        helper(new char[n][n], 0, n);
        return res;
    }
    
    private void helper(char[][] board, int layer, int n) {
        if (layer >= n) {
            List<String> curr = new ArrayList<>();
            for (char[] chs : board) curr.add(new String(chs));
            res.add(curr);
            return;
        }
        Arrays.fill(board[layer], '.');
        for (int j = 0; j < n; j++) {
            if (col[j] == 1 || diag1[layer + j] == 1 || diag2[layer - j + n - 1] == 1) continue;
            col[j] = 1;
            diag1[layer + j] = 1;
            diag2[layer - j + n - 1] = 1;
            board[layer][j] = 'Q';
            helper(board, layer + 1, n);
            board[layer][j] = '.';
            diag2[layer - j + n - 1] = 0;
            diag1[layer + j] = 0;
            col[j] = 0;   
        }
    }