图论-最短路径 floyd/dijkstra-Find the City With the Smallest Number of Neighbors at a Threshold Distance
2020-01-30 22:22:58
问题描述:

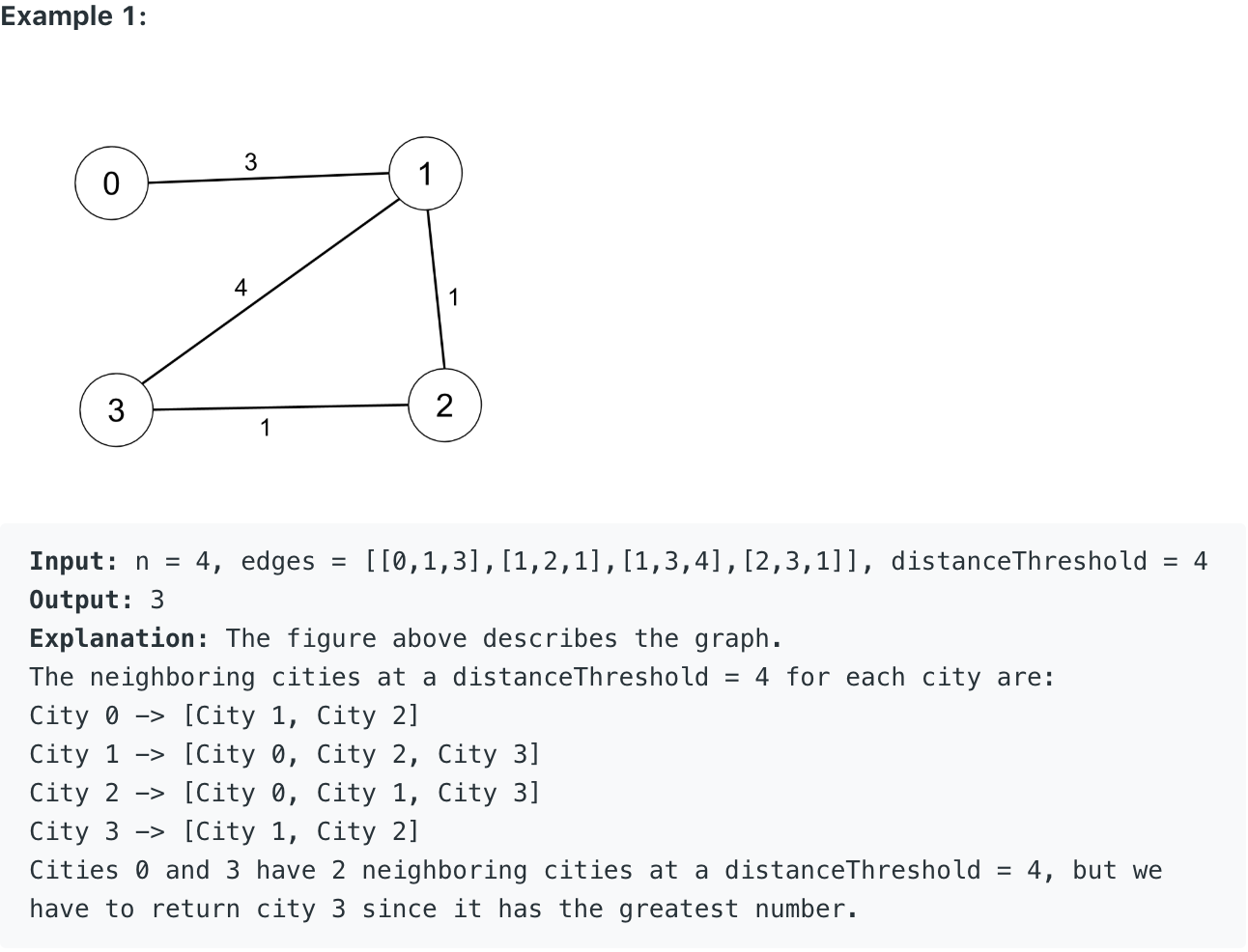

问题求解:
解法一:floyd
这个题目一看就是floyd解最合适,因为是要求多源最短路,floyd算法是最合适的,时间复杂度为O(n ^ 3)。
int inf = (int)1e9;
public int findTheCity(int n, int[][] edges, int distanceThreshold) {
int[][] dp = new int[n][n];
for (int i = 0; i < n; i++) Arrays.fill(dp[i], inf);
for (int i = 0; i < n; i++) {
dp[i][i] = 0;
}
for (int[] edge : edges) {
int u = edge[0];
int v = edge[1];
int d = edge[2];
dp[u][v] = d;
dp[v][u] = d;
}
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (dp[i][j] > dp[i][k] + dp[k][j]) {
dp[i][j] = dp[i][k] + dp[k][j];
}
}
}
}
List<int[]> note = new ArrayList<>();
for (int i = 0; i < n; i++) {
int cnt = 0;
for (int j = 0; j < n; j++) {
if (dp[i][j] <= distanceThreshold) cnt += 1;
}
note.add(new int[]{i, cnt});
}
Collections.sort(note, new Comparator<int[]>(){
public int compare(int[] o1, int[] o2) {
return o1[1] == o2[1] ? o2[0] - o1[0] : o1[1] - o2[1];
}
});
return note.get(0)[0];
}
解法二:dijkstra
使用邻接表 + 优先队列可以将单源最短路的时间复杂度降到O(ElogV),所以整体的时间复杂度为O(VElogV)。
public int findTheCity(int n, int[][] edges, int distanceThreshold) {
List<int[]> record = new ArrayList<>();
List<int[]>[] graph = new List[n];
for (int i = 0; i < n; i++) graph[i] = new ArrayList<>();
for (int[] edge : edges) {
int from = edge[0];
int to = edge[1];
int w = edge[2];
graph[from].add(new int[]{to, w});
graph[to].add(new int[]{from, w});
}
for (int i = 0; i < n; i++) {
int[] dist = new int[n];
Arrays.fill(dist, (int)1e9);
helper(graph, i, dist);
int cnt = 0;
for (int j = 0; j < n; j++) if (dist[j] <= distanceThreshold) cnt += 1;
record.add(new int[]{i, cnt});
}
Collections.sort(record, (int[] o1, int[] o2) -> o1[1] == o2[1] ? o2[0] - o1[0] : o1[1] - o2[1]);
return record.get(0)[0];
}
private void helper(List<int[]>[] graph, int node, int[] dist) {
int n = graph.length;
PriorityQueue<int[]> pq = new PriorityQueue<>((int[] o1, int[] o2) -> o1[1] - o2[1]);
int[] used = new int[n];
pq.add(new int[]{node, 0});
while (!pq.isEmpty()) {
int[] curr = pq.poll();
int from = curr[0];
int d = curr[1];
if (used[from] == 1) continue;
used[from] = 1;
dist[from] = d;
for (int[] next : graph[from]) {
int to = next[0];
int w = next[1];
if (dist[to] > dist[from] + w) {
dist[to] = dist[from] + w;
pq.add(new int[]{to, dist[to]});
}
}
}
}



