BIT-Count of Range Sum

2019-12-17 18:56:56

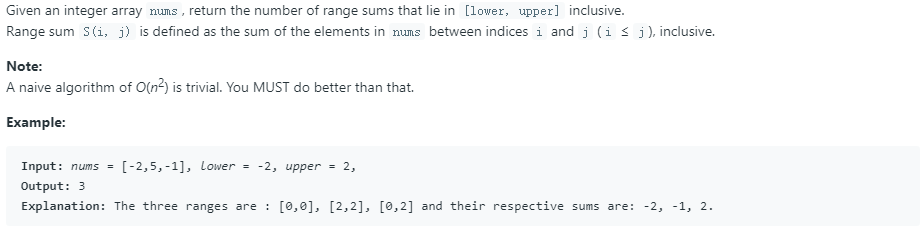
问题描述：

问题求解：

本题个人感觉还是很有难度的，主要的难点在于如何将题目转化为bit计数问题。

首先构建一个presum数组，这个没有问题。

需要对于任意一个j，我们需要知道的是presum[i]的个数使得 lower <= presum[j] - presum[i] <= upper。

上述等式等价于求符合 presum[j] - upper <= presum[i] <= presum[j] - lower 的presum[i]的个数。

看到这个是不是有点眼熟了呢，求满足某个条件的区间的个数，这个和逆序数问题是完全一致的，只是在那个问题里我们只有一个上界，这里多了一个下界罢了。

同逆序数的解法，这里我们可以使用树状数组来进行求解。

    public int countRangeSum(int[] nums, int lower, int upper) {
        if (nums.length == 0) return 0;
        int res = 0;
        int n = nums.length;
        long[] presum = new long[n];
        presum [0] = nums[0];
        for (int i = 1; i < n; i++) presum[i] = presum[i - 1] + nums[i];
        long[] copy = Arrays.copyOf(presum, n);
        Arrays.sort(copy);
        TreeMap<Long, Integer> map = new TreeMap<>();
        int rank = 0;
        for (int i = 0; i < n; i++) {
            if (i == 0 || copy[i] != copy[i - 1]) {
                map.put(copy[i], ++rank);
            }
        }
        int[] bit = new int[map.size() + 1];
        for (int i = 0; i < n; i++) {
            if (presum[i] >= lower && presum[i] <= upper) res += 1;
            Long r = map.floorKey(presum[i] - lower);
            Long l = map.ceilingKey(presum[i] - upper);
            if (l != null && r != null) res += query(bit, map.get(r)) - query(bit, map.get(l) - 1); 
            update(bit, map.get(presum[i]));
        }
        return res;
    }
    
    private void update(int[] bit, int idx) {
        for (int i = idx; i < bit.length; i += i & -i) {
            bit[i] += 1;
        }
    }
    
    private int query(int[] bit, int idx) {
        int res = 0; 
        for (int i = idx; i > 0; i -= i & -i) {
            res += bit[i];
        }
        return res;
    }