进制-Iterative-进制转换

2019-12-02 21:15:31

进制转换是计算机科学里的一个基础算法，通常可以使用如下的模版来进行计算。

下面我们来讨论一些关于进制的题目。

• 1271. Hexspeak 

问题描述：

 

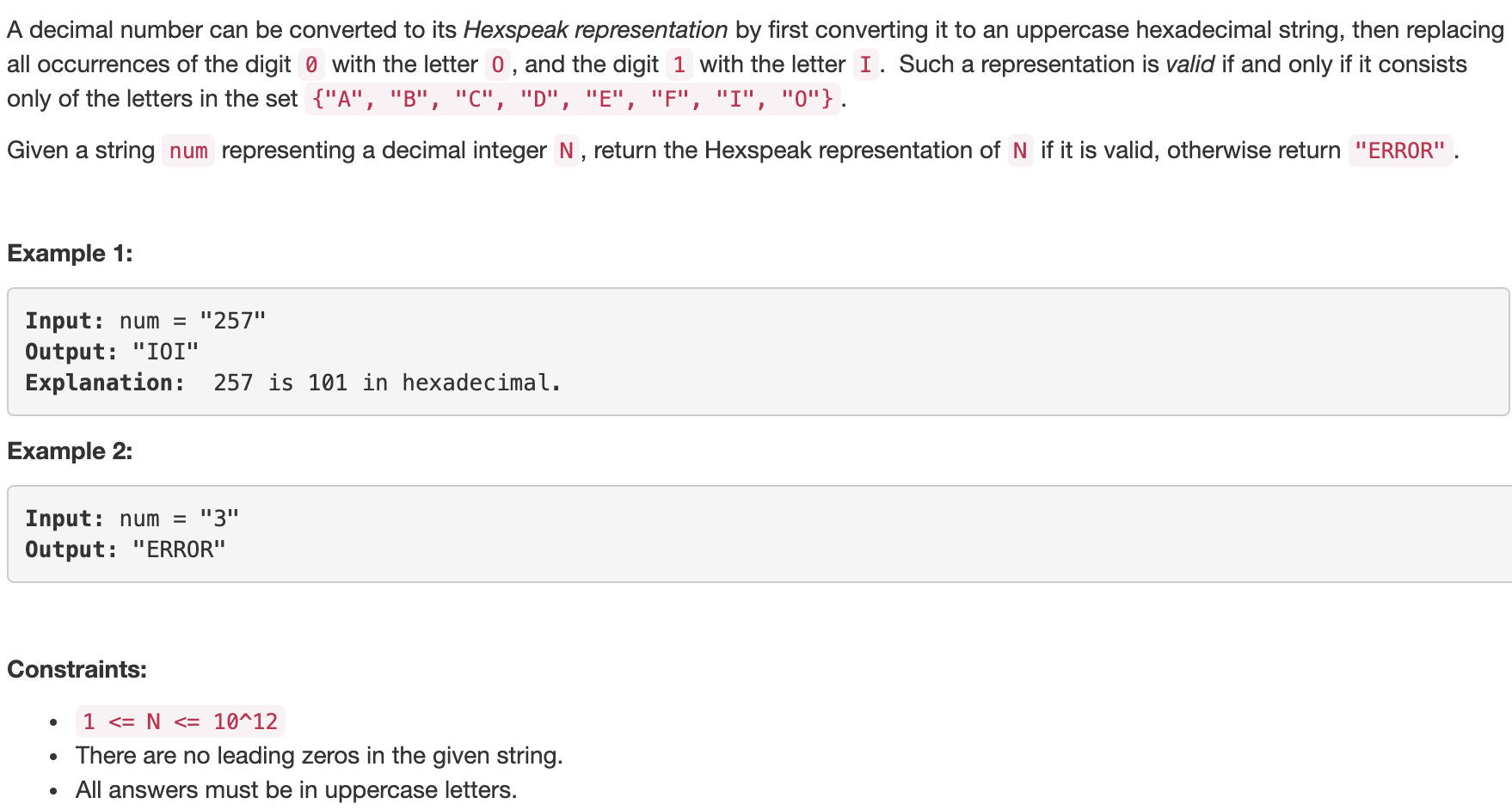
问题求解：

    public String toHexspeak(String num) {
        StringBuffer sb = new StringBuffer();
        char[] chs = new char[]{'A', 'B', 'C', 'D', 'E', 'F'};
        long n = Long.valueOf(num);
        while (n > 0) {
            int d = (int)(n % 16);
            if (d == 1) sb.append("I");
            else if (d == 0) sb.append("O");
            else if (d > 1 && d <= 9) return "ERROR";
            else sb.append(chs[d - 10]);
            n = n / 16;
        }
        return sb.reverse().toString();
    }

　

• 504. Base 7

问题描述：

问题求解：

    public String convertToBase7(int num) {
        if (num == 0) return "0";
        StringBuffer sb = new StringBuffer();
        boolean flag = num >= 0;
        num = num >= 0 ? num : -num;
        while (num > 0) {
            int d = num % 7;
            sb.append(d);
            num = num / 7;
        }
        return flag ? sb.reverse().toString() : "-" + sb.reverse().toString();
    }

 

• 1017. Convert to Base -2

问题描述：

问题求解：

在计算机科学中，在对负数取余数的时候，当除数和被除数都是负数的时候，得到的余数也将是负数

-3 / -2 = 1    -3 % -2 = -1
3 / -2 = -1    3 % -2 = 1

在本题中需要所有的余数都是正数的，所以在计算的时候做了一些trick变换。

    public String baseNeg2(int N) {
        if (N == 0) return "0";
        StringBuffer sb = new StringBuffer();
        while (N != 0) {
            int d = N % -2;
            if (d == -1) {
                sb.append(1);
                N = N / -2 + 1;
            }
            else {
                sb.append(d);
                N = N / -2;
            }
        }
        return sb.reverse().toString();
    }