2018-12-09 22:18:43
假设费用函数 L 与某个参数 x 的关系如图所示：
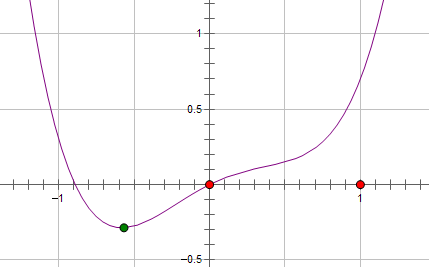
则最优的 x 在绿点处，x 非零。
现在施加 L2 regularization，新的费用函数（
）如图中蓝线所示：
最优的 x 在黄点处，x 的绝对值减小了，但依然非零。
而如果施加 L1 regularization，则新的费用函数（
）如图中粉线所示：
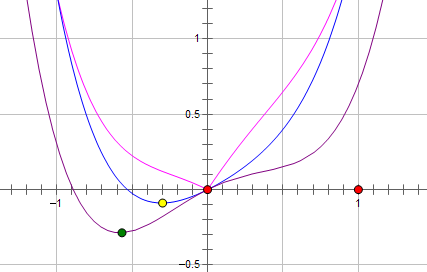
最优的 x 就变成了 0。这里利用的就是绝对值函数的尖峰。
两种 regularization 能不能把最优的 x 变成 0，取决于原先的费用函数在 0 点处的导数。
如果本来导数不为 0，那么施加 L2 regularization 后导数依然不为 0，最优的 x 也不会变成 0。
而施加 L1 regularization 时，只要 regularization 项的系数 C 大于原先费用函数在 0 点处的导数的绝对值，x = 0 就会变成一个极小值点。原因是我们可以对0两边进行求导分别得到f'(0) - C和f‘(0) + C，如果C > f'(0)，那么左右两边就会异号，这样的话，0就成了极小值点了。
上面只分析了一个参数 x。事实上 L1 regularization 会使得许多参数的最优值变成 0，这样模型就稀疏了。
