评价分类器的好坏

2018-12-06 17:05:27

这里以二分类举例，首先引入混淆矩阵的概念：

混淆矩阵是一个2×2的方阵，用于展示分类器预测的结果——真正（true positive），假负（false negative）、假正（false positive）及假负（false negative）

下面介绍一下各个评价指标：

正确率(Accuracy，ACC)：正确率是最容易理解的，就是预测正确的样本占样本总数的比例。

ACC = (TP + TN) / (TP + TN + FP + FN)

错误率(Error，ERR)：错误率显然就是1 - ACC，换句话说，就是预测错误的样本占样本总数的比例。

ERR = (FP + FN) / (FP + FN + TP + TN)

查准率/精确率(Precision，PRE)：精确率是指预测为正的样本中到底有多少确实是正样本。

PRE = TP / (TP + FP)

召回率(Recall，REC)：召回率是指预测正确的正样本数量占总体正样本数量的比例。

REC = TP / (TP + FN)

ROC曲线：

如正样本有90个，负样本有10个，直接把所有样本分类为正样本，得到识别率为90%，但这显然是没有意义的。因此就引入了ROC曲线的概念。

纵轴为真正类率(true positive rate，TPR)，预测正确的正类占总体正类的比例 :

TPR = TP / (TP + FN)

横轴为真负类率(True Negative Rate，TNR)，错误被预测为正类的样本占总体负样本的比例 :

FPR = FP / (FP + TN)

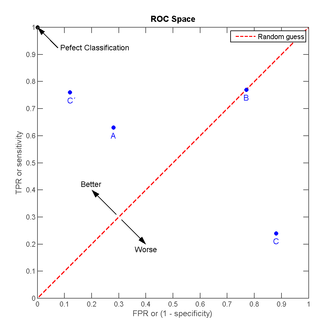
我们可以看出：左上角的点（TPR=1，FPR=0），为完美分类，也就是这个医生医术高明，诊断全对；点A（TPR>FPR），医生A的判断大体是正确的。中线上的点B（TPR=FPR），也就是医生B全都是蒙的，蒙对一半，蒙错一半；下半平面的点C（TPR<FPR），这个医生说你有病，那么你很可能没有病，医生C的话我们要反着听，为真庸医。

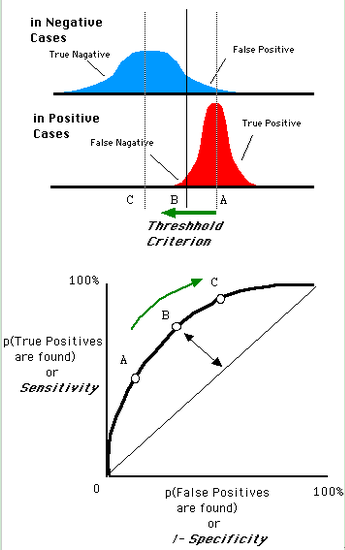
一个阈值，得到一个点。现在我们需要一个独立于阈值的评价指标来衡量这个医生的医术如何，也就是遍历所有的阈值，得到ROC曲线。还是一开始的那幅图，假设如下就是某个医生的诊断统计图，直线代表阈值。我们遍历所有的阈值，能够在ROC平面上得到如下的ROC曲线。

AUC :

AUC值为ROC曲线所覆盖的区域面积，显然，AUC越大，分类器分类效果越好。

• AUC = 1，是完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。
• 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
• AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
• AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。