最多的划分来使数组有序 Max Chunks To Make Sorted

2018-12-01 11:05:46

一、Max Chunks To Make Sorted

问题描述：

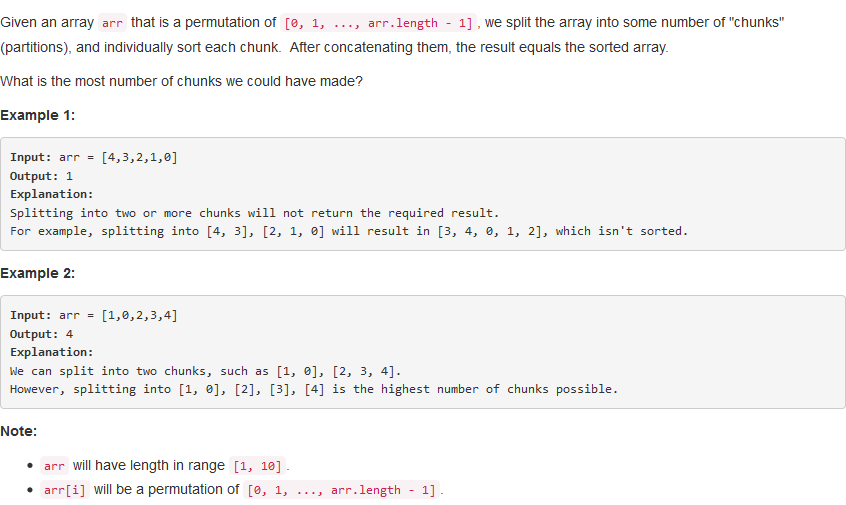
问题求解：

由于没有重复，所以直观的来看对于每个遇到数，其能够被划分出来的前提是其前面已经有相应的数字，具体可以看下面的图片。

    public int maxChunksToSorted(int[] arr) {
        if (arr == null || arr.length == 0) return 0;
        int res = 0;
        int curMax = arr[0];
        for (int i = 0; i < arr.length; i++) {
            curMax = Math.max(curMax, arr[i]);
            if (curMax == i) res++;
        }
        return res;
    }

 

二、Max Chunks To Make Sorted II

问题描述：

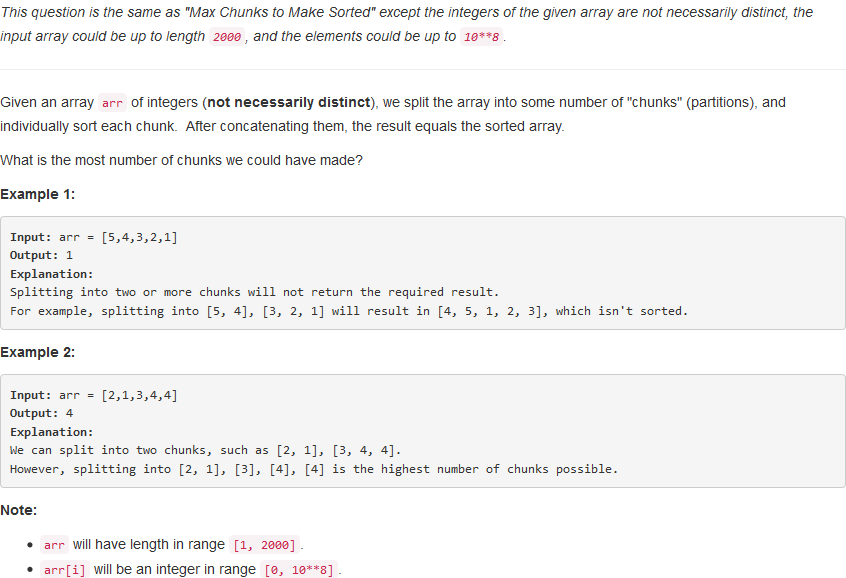
问题求解：

本题是上一题的扩展，可以说是普通化的上一题，由于数字范围以及重复性，难度有了较大的提升，显然是不能直接使用上述的解法了，如果进行离散化，那么至少是O(nlogn)的时间复杂度，有没有O(n)的解法呢？

答案是有的，但是看问题的角度要变化一下，我们可以这么来看这个问题，从左向右遍历整个数组，如果说当前的数字的左边的最大值小于其右边的最小值，那么将这个数和左边进行排序是没有风险的，重复进行这样的操作就可以得到最终的结果。

可以使用两个数组来对左侧最大值和右侧最小值进行保存，整个时间复杂度显然是O(n)。

    public int maxChunksToSorted(int[] arr) {
        if (arr == null || arr.length == 0) return 0;
        int[] maxofleft = new int[arr.length];
        int[] minofright = new int[arr.length];
        maxofleft[0] = arr[0];
        for (int i = 0; i < arr.length; i++) {
            maxofleft[i] = Math.max(maxofleft[i - 1], arr[i]);
        }
        minofright[arr.length - 1] = arr[arr.length - 1];
        for (int i = arr.length - 2; i >= 0; i--) {
            minofright[i] = Math.min(minofright[i + 1], arr[i]);
        }
        int res = 0;
        for (int i = 0; i < arr.length - 1; i++) {
            if (maxofleft[i] <= minofright[i + 1]) res++;
        }
        return res + 1;
    }

 

三、Partition Labels

问题描述：

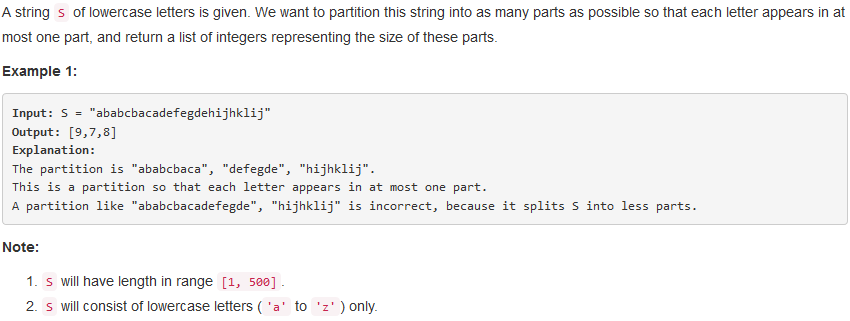
问题求解：

本题的要求是将一个字符串划分成尽量多的子串，并且保证同一个字符只出现在其中一个子串中。

从直观上来看，我们可以暴力的进行求解，也就是对第一字符进行判断，将其最后出现的位置做标定，如果当前的idx和最后出现位置相同，那么就找到了一个划分，否则对第二个字符进行判断，寻找其最后一个字符出现的位置，并更新最后的位置，重复当前操作即可。

如果暴力检索，那么时间复杂度显然是O(n^2)，如果进行预处理，将一个字符的最后出现位置保存下来，那么时间复杂度就可以将到O(n)。

    public List<Integer> partitionLabels(String S) {
        List<Integer> res = new ArrayList<>();
        int[] map = new int[128];
        for (int i = 0; i < S.length(); i++) {
            map[S.charAt(i)] = i;
        }
        int begin = 0;
        int end = 0;
        for (int i = 0; i < S.length(); i++) {
            end = Math.max(end, map[S.charAt(i)]);
            if (end == i) {
                res.add(end - begin + 1);
                begin = end + 1;
            }
        }
        return res;
    }