HDU - 3407 - String-Matching Automata

先上题目：

String-Matching Automata

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 215    Accepted Submission(s): 140

Problem Description

The finite state automaton (FSA) is an important model of behavioral investigations in computer science, linguistics and many other areas. A FSA can be typically modeled as a string pattern recognizer described by a quintuple <Σ, S, s0, δ, F>, where:

Σ is the input alphabet (a finite nonempty set of symbols).
S is a finite nonempty set of states.
s0 is an element in S designated as the initial state.
δ is a function δ: S × Σ → S known as the transition function.
F is a (possibly empty) subset of S whose elements are designated as the final states.

An FSA with the above description operates as follows:

At the beginning, the automaton starts in the initial state s0.
The automaton continuously reads symbols from its input, one symbol at a time, and transits between states according to the transition function δ. To be specific, let s be the current state and w the symbol just read, the automaton moves to the state given by δ(s, w).
When the automaton reaches the end of the input, if the current state belongs to F, the string consisting sequentially of the symbols read by the automaton is declared accepted, otherwise it is declared rejected.

Just as the name implies, a string-matching automaton is a FSA that is used for string matching and is very efficient: they examine each character exactly once, taking constant time per text character. The matching time used (after the automaton is built) is therefore Θ(n). However, the time to build the automaton can be large.

Precisely, there is a string-matching automaton for every pattern P that you search for in a given text string T. For a given pattern of length m, the corresponding automaton has (m + 1) states {q0, q1, …, qm}: q0 is the start state, qm is the only final state, and for each i in {0, 1, …, m}, if the automaton reaches state qi, it means the length of the longest prefix of P that is also a suffix of the input string is i. When we reaches state qm, it means P is a suffix of the currently input string, which suggest we find an occurrence of P.

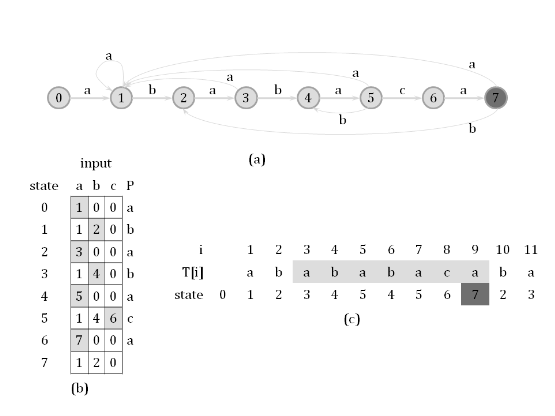
The following graph shows a string-matching automaton for the pattern “ababaca”, and illustrates how the automaton works given an input string “abababacaba”.



Apparently, the matching process using string-matching automata is quite simple (also efficient). However, building the automaton efficiently seems to be tough, and that’s your task in this problem.

 

 

Input

Several lines, each line has one pattern consist of only lowercase alphabetic characters. The length of the longest pattern is 10000. The input ends with a separate line of ‘0’.

 

 

Output

For each pattern, output should contain (m + 1) lines(m is the length of the pattern). The nth line describes how the automaton changes its state from state (n-1) after reading a character. It starts with the state number (n – 1), and then 26 state numbers follow. The 1st state number p1 indicates that when the automaton is in state (n-1), it will transit to state p1 after reading a character ‘a’. The 2nd state number p2 indicates that when the automaton is in state (n-1), it will transit to state p2 after reading a character ‘b’… And so on.

 

 

Sample Input

ababaca 0

 

 

Sample Output

0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

1 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

2 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

3 1 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

4 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

5 1 4 6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

6 7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

7 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

 

Source

2010 National Programming Invitational Contest Host by ZSTU

 

　　题意：给你一个串，问你当匹配到某个位置的时候如果当匹配的字母为'a'-'z'的时候分别需要转移的位置是哪里？

 

　　解法可以用KMP+一点其他操作。另一种方法是直接写一个AC自动机，然后build了自动机以后就沿着Trie树上输入的单词对于某一个节点就直接打印这个节点的next[i]['a'~'z']就可以了。

 

上代码：

 

#include <cstdio>
#include <cstring>
#include <queue>
#define MAX 10002
using namespace std;

struct Trie{
    int next[MAX][26],fail[MAX],end[MAX],num[MAX][26];
    int root,L;

    int newnode(){
        for(int i=0;i<26;i++){ next[L][i]=-1; num[L][i]=0;}
        end[L++]=0;
        return L-1;
    }
    void init(){
        L=0;    root=newnode();
    }

    void insert(char buf[]){
        int len=strlen(buf);
        int now = root;
        for(int i=0;i<len;i++){
            if(next[now][buf[i]-'a']==-1){
                next[now][buf[i]-'a']=newnode();

            }
            now=next[now][buf[i]-'a'];
        }
        end[now]++;
    }

    void build(){
        queue<int> Q;
        fail[root]=root;
        for(int i=0;i<26;i++){
            if(next[root][i]==-1) next[root][i]=root;
            else{
                fail[next[root][i]]=root;
                Q.push(next[root][i]);
            }
        }
        while(!Q.empty()){
            int now=Q.front();
            Q.pop();
            for(int i=0;i<26;i++){
                if(next[now][i]==-1) next[now][i]=next[fail[now]][i];
                else{
                    fail[next[now][i]]=next[fail[now]][i];
                    Q.push(next[now][i]);
                }
            }
        }
    }

    void print(char buf[]){
        int len=strlen(buf);
        int now=root;
        for(int i=0;i<=len;i++){
            printf("%d",i);
            for(int j=0;j<26;j++) printf(" %d",next[now][j]);
            printf("\n");
            now=next[now][buf[i]-'a'];
        }
    }
};

Trie ac;
char s[MAX];

int main()
{
    //freopen("data.txt","r",stdin);
    while(scanf("%s",s),strcmp(s,"0")){
        ac.init();
        ac.insert(s);
        ac.build();
        ac.print(s);//printf("\n");
    }
    return 0;
}