HDU - 2973 - YAPTCHA
先上题目:
YAPTCHA
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 463 Accepted Submission(s): 280
Problem Description
The
math department has been having problems lately. Due to immense amount
of unsolicited automated programs which were crawling across their
pages, they decided to put
Yet-Another-Public-Turing-Test-to-Tell-Computers-and-Humans-Apart on
their webpages. In short, to get access to their scientific papers, one
have to prove yourself eligible and worthy, i.e. solve a mathematic
riddle.
However, the test turned out difficult for some math PhD students and even for some professors. Therefore, the math department wants to write a helper program which solves this task (it is not irrational, as they are going to make money on selling the program).
The task that is presented to anyone visiting the start page of the math department is as follows: given a natural n, compute
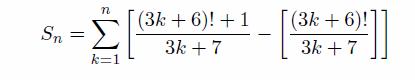
where [x] denotes the largest integer not greater than x.
However, the test turned out difficult for some math PhD students and even for some professors. Therefore, the math department wants to write a helper program which solves this task (it is not irrational, as they are going to make money on selling the program).
The task that is presented to anyone visiting the start page of the math department is as follows: given a natural n, compute
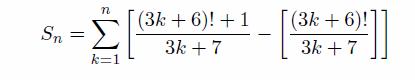
where [x] denotes the largest integer not greater than x.
Input
The
first line contains the number of queries t (t <= 10^6). Each query
consist of one natural number n (1 <= n <= 10^6).
Output
For each n given in the input output the value of Sn.
Sample Input
13
1
2
3
4
5
6
7
8
9
10
100
1000
10000
Sample Output
0 1 1 2 2 2 2 3 3 4 28 207 1609
题意很简单,t个case,每个case给你一个n,根据公式求出结果然后直接输出结果。
先说一下这一题需要用到什么,一是筛素数,二是威尔逊定理。
威尔逊定理如下:
p是素数,则 (p-1)! ≡ -1 (mod p)
为什么需要用到威尔逊定理,通过观察题目给出的公式可以令p=3k+7,则通过分析,当p为素数的时候Sn中第k个数就是1,否则p不是素数的时候第k个数就是0。所以才需要筛素数,然后再判断给出的范围里面每一个Sn,然后每一次查询就直接输出答案。
在ac之前wa了两次,后来发现是数组开小了= =了,所以这里开大100其实没有关系。
代码上两份,一份是完全自己写的,筛素数的时间复杂度为nloglogn,提交以后返回的时间是800+ms,另一份是用上人家的输入输出挂,速度会去到200+ms,染过吧筛素数的方法换成线性筛法的话还会快大概30ms。
上代码:

#include <stdio.h> #include <string.h> #define MAX 1000110 using namespace std; bool pri[MAX*3]; int ans[MAX]; void dedeal() { long long i,j,n; n=(MAX-10)*3; memset(pri,0,sizeof(pri)); pri[0]=pri[1]=1; for(i=2;i<=n;i++) { if(!pri[i]) for(j=i*i;j<=n;j+=i) pri[j]=1; } } void deal() { int i,n; n=(MAX-10); memset(ans,0,sizeof(ans)); for(i=1;i<=n;i++) { if(!pri[3*i+7]) ans[i]=ans[i-1]+1; else ans[i]=ans[i-1]; } } int main() { int n,t; //freopen("data.txt","r",stdin); dedeal(); deal(); scanf("%d",&t); while(t--) { scanf("%d\n",&n); printf("%d\n",ans[n]); } return 0; }
提速版

1 #include <iostream> 2 #include <string.h> 3 #include <stdio.h> 4 #define MAX 1000110 5 using namespace std ; 6 bool pri[3000008] ; 7 int ans[1000001] ; 8 9 10 void dedeal() 11 { 12 long long i,j,n; 13 n=(MAX-10)*3; 14 memset(pri,0,sizeof(pri)); 15 pri[0]=pri[1]=1; 16 for(i=2;i<=n;i++) 17 { 18 if(!pri[i]) 19 for(j=i*i;j<=n;j+=i) pri[j]=1; 20 } 21 } 22 23 void deal() 24 { 25 int i,n; 26 n=(MAX-10); 27 memset(ans,0,sizeof(ans)); 28 for(i=1;i<=n;i++) 29 { 30 if(!pri[3*i+7]) 31 ans[i]=ans[i-1]+1; 32 else ans[i]=ans[i-1]; 33 } 34 } 35 36 37 inline bool scan_d(int &num) 38 { 39 char in;bool IsN=false; 40 in=getchar(); 41 if(in==EOF) return false; 42 while(in!='-'&&(in<'0'||in>'9')) in=getchar(); 43 if(in=='-'){ IsN=true;num=0;} 44 else num=in-'0'; 45 while(in=getchar(),in>='0'&&in<='9'){ 46 num*=10,num+=in-'0'; 47 } 48 if(IsN) num=-num; 49 return true; 50 } 51 52 void print_f(int x){ 53 if(x==0)return; 54 print_f(x/10); 55 putchar(x%10+'0'); 56 } 57 int main() 58 { 59 //freopen("data.txt","r",stdin); 60 int t ; 61 dedeal(); 62 deal(); 63 scan_d(t) ; 64 while(t--) 65 { 66 int n ; 67 scan_d(n) ; 68 if(n==1) 69 putchar('0') ; 70 else 71 print_f(ans[n]) ; 72 putchar('\n') ; 73 } 74 return 0 ; 75 }




