Atan2
在三角函数中,两个参数的函数atan2是正切函数的 一个变种。对于任意不同时等于0的实参数x和y,atan2(y,x)所表达的意思是坐标原点为起点,指向(x,y)的射线在坐标平面上与x轴正方向之间 的角的角度。当y>0时,射线与x轴正方向的所得的角的角度指的是x轴正方向绕逆时针方向到达射线旋转的角的角度;而当y<0时,射线与x轴 正方向所得的角的角度指的是x轴正方向绕顺时针方向达到射线旋转的角的角度。
在几何意义上,atan2(y, x) 等价于 atan(y/x),但 atan2 的最大优势是可以正确处理 x=0 而 y≠0 的情况,而不必进行会引发除零异常的 y/x 操作。
atan2函数最初在计算机编程语言中被引入,但是现在它的应用在科学和工程等其他多个领域十分常见。他的出现最早可以追溯到FORTRAN语言[1],并且可以在C语言的数学标准库的math.h文件中找到,此外在Java数学库、.NET的System.Math(可应用于C#、VB.NET等语言)、Python的数学模块以及其他地方都可以找到atan2的身影。许多脚本语言,比如Perl,也包含了C语言风格的atan2函数[2]。
目录
工作原理
函数定义
基于值域为 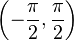 的正切函数,该函数定义如下:
的正切函数,该函数定义如下:
说明:
- 该函数的值域为
![\left ( -\pi,\pi \right ]](http://upload.wikimedia.org/math/8/4/0/8408d4ba9bd6eb98310e12bbbf13825f.png) ,可以通过对负数结果加
,可以通过对负数结果加 的方法,将函数的结果映射到
的方法,将函数的结果映射到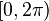 范围内。
范围内。
其他软件中的变形
有关图片

旁边的图片显示内容是:在一个单位圆内atan2函数在各点的取值。圆内标注代表各点的取值的幅度表示。
图片中,从最左端开始,角度的大小随着逆时针方向逐渐从-π增大到+π,并且角度大小在点位于最右端时,取值为0。
另外要注意的是,函数atan2(y,x)中参数的顺序是倒置的,atan2(y,x)计算的值相当于点(x,y)的角度值。
下方的图片显示的是单位圆上各点在atan2函数上的值,从原点射向(0,1)点的射线,开始绕逆时针方向可以与x轴正方向得到对应各点的复平面的复角,其中几个特殊点取值:
- (0, 1)对于的复平面夹角为π/2,
- (−1, 0)对于复平面的夹角为π,
- (0, −1)对于复平面的夹角为3π/2,
在回到(1, 0)复平面夹角为 0 = (2nπ mod 2π)。
这些你可以直观的从图中看出。[3]

下面的插图分别显示的是atan2(y,x)和atan(y,x)在坐标平面的三维景象。
注意在atan2(y,x)函数中,从原点辐射出的射线上有常数值,而在atan(y/x)的函数中,经过原点的直线有常数值。


参考文献
- ^ Organick, Elliott I. A FORTRAN IV Primer. Addison-Wesley. 1966: 42. "Some processors also offer the library function called ATAN2, a function of two arguments (opposite and adjacent)."
- ^ The Linux Programmer's Manual [1] says:
- "The atan2() function calculates the arc tangent of the two variables y and x. It is similar to calculating the arc tangent of y / x, except that the signs of both arguments are used to determine the quadrant of the result."
- ^ Computation of the external argument by Wolf Jung





 浙公网安备 33010602011771号
浙公网安备 33010602011771号