POJ1390 Blocks(DP、记忆化搜索)
题目链接:
http://poj.org/problem?id=1390
题目描述:
Blocks
Description
Some of you may have played a game called 'Blocks'. There are n blocks in a row, each box has a color. Here is an example: Gold, Silver, Silver, Silver, Silver, Bronze, Bronze, Bronze, Gold.
The corresponding picture will be as shown below:
![]()
Figure 1
If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a 'box segment'. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1 box(es) in the segments respectively.
Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get k*k points. for example, if you click on a silver box, the silver segment disappears, you got 4*4=16 points.
Now let's look at the picture below:
![]()
Figure 2
The first one is OPTIMAL.
Find the highest score you can get, given an initial state of this game.
The corresponding picture will be as shown below:

Figure 1
If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a 'box segment'. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1 box(es) in the segments respectively.
Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get k*k points. for example, if you click on a silver box, the silver segment disappears, you got 4*4=16 points.
Now let's look at the picture below:
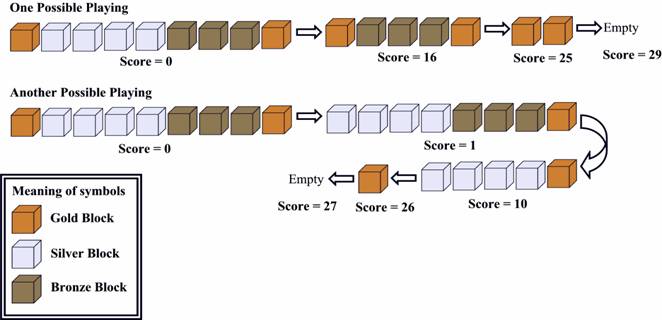
Figure 2
The first one is OPTIMAL.
Find the highest score you can get, given an initial state of this game.
Input
The first line contains the number of tests t(1<=t<=15). Each case contains two lines. The first line contains an integer n(1<=n<=200), the number of boxes. The second line contains n integers, representing the colors of each box. The integers are in the range 1~n.
Output
For each test case, print the case number and the highest possible score.
Sample Input
2 9 1 2 2 2 2 3 3 3 1 1 1
Sample Output
Case 1: 29 Case 2: 1
题目大意:
同种颜色的块块可以消除,每次得分是数量的平方,求最大得分
思路:
一看是个dp题目
先缩点,记录 color 和 len, 设计状态 dp[ i ][ j ][ k ] 表示第 i 到 j 段的最大得分,其中第 j 段和从右边过来的 k 个长度的同种颜色一起消除了
保证 j 和 k 之间在之前被消除
状态转移方程为
dp[l][r][k] =
max( dp[ l ][ r - 1 ][ 0 ] + (k + len[r])*(k + len[r]), max{ dp[ l ][ i ][ len[r] + k ] + dp[ i + 1 ][ r - 1 ][ 0 ] } )
其中 r > i >= L
然后记忆化搜索即可
代码:
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 using namespace std; 6 7 const int N = 210; 8 9 int n, c[N], len[N], dp[N][N][N]; 10 11 int solve(int l, int r, int k) { 12 if (dp[l][r][k])return dp[l][r][k]; 13 if (l == r)return dp[l][r][k] = (len[r] + k)*(len[r] + k); 14 dp[l][r][k] = solve(l, r - 1, 0) + (k + len[r])*(k + len[r]); 15 for (int i = l; i < r; ++i)if (c[i] == c[r]) 16 dp[l][r][k] = max(dp[l][r][k], solve(l, i, len[r] + k) + solve(i + 1, r - 1, 0)); 17 return dp[l][r][k]; 18 } 19 20 int main() { 21 int t, ca = 0; 22 scanf("%d", &t); 23 while (t--) { 24 memset(dp, 0, sizeof(dp)); 25 scanf("%d", &n); 26 int a[N]; 27 for (int i = 0; i < n; ++i) 28 scanf("%d", &a[i]); 29 int q = 0; 30 for (int i = 0; i < n; ++i) { 31 if (i&&a[i] == a[i - 1])++len[q]; 32 else c[++q] = a[i], len[q] = 1; 33 } 34 printf("Case %d: %d\n", ++ca, solve(1, q, 0)); 35 } 36 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号