POJ2194 Stacking Cylinders(向量旋转)
题目链接:
http://poj.org/problem?id=2194
题目描述:
Stacking Cylinders
Description
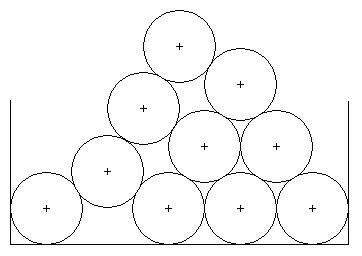
Cylinders (e.g. oil drums) (of radius 1 foot) are stacked in a rectangular bin. Each cylinder on an upper row rests on two cylinders in the row below. The cylinders in the bottom row rest on the floor. Each row has one less cylinder than the row below.
![]()
This problem is to write a program to compute the location of the center of the top cylinder from the centers of the cylinders on the bottom row. Computations of intermediate values should use double precision.
This problem is to write a program to compute the location of the center of the top cylinder from the centers of the cylinders on the bottom row. Computations of intermediate values should use double precision.
Input
Each data set will appear in one line of the input. An input line consists of the number, n, of cylinders on the bottom row followed by n floating point values giving the x coordinates of the centers of the cylinders (the y coordinates are all 1.0 since the cylinders are resting on the floor (y = 0.0)). The value of n will be between 1 and 10 (inclusive). The end of input is signaled by a value of n = 0. The distance between adjacent centers will be at least 2.0 (so the cylinders do not overlap) but no more than 3.4 (cylinders at level k will never touch cylinders at level k – 2).
Output
The output for each data set is a line containing the x coordinate of the topmost cylinder rounded to 4 decimal places, a space and the y coordinate of the topmost cylinder to 4 decimal places. Note: To help you check your work, the x-coordinate of the center of the top cylinder should be the average of the x-coordinates of the leftmost and rightmost bottom cylinders.
Sample Input
4 1.0 4.4 7.8 11.2 1 1.0 6 1.0 3.0 5.0 7.0 9.0 11.0 10 1.0 3.0 5.0 7.0 9.0 11.0 13.0 15.0 17.0 20.4 5 1.0 4.4 7.8 14.6 11.2 0
Sample Output
6.1000 4.1607 1.0000 1.0000 6.0000 9.6603 10.7000 15.9100 7.8000 5.2143
题目大意:
圆从最底层开始摞,求最上面的球的横纵坐标
思路:
枚举层
用当前层两个相邻圆去构造新圆
很容易可以求出圆心夹角
旋转向量即可
代码:
1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #include <cmath> 5 #include <cstring> 6 using namespace std; 7 8 const int N = 12; 9 const double EPS = 1e-10; //精度系数 10 const double PI = acos(-1.0); //π 11 12 struct Point { 13 double x, y; 14 Point(double x = 0, double y = 0) :x(x), y(y) {} 15 const bool operator < (Point A)const { 16 return x == A.x ? y < A.y : x < A.x; 17 } 18 }; //点的定义 19 20 typedef Point Vector; //向量的定义 21 22 Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); } //向量加法 23 Vector operator - (Vector A, Vector B) { return Vector(A.x - B.x, A.y - B.y); } //向量减法 24 Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); } //向量数乘 25 26 int dcmp(double x) { 27 if (fabs(x) < EPS)return 0; else return x < 0 ? -1 : 1; 28 } //与0的关系 29 30 Vector Rotate(Vector A, double rad) { 31 return Vector(A.x*cos(rad) - A.y*sin(rad), A.x*sin(rad) + A.y*cos(rad)); 32 } //逆时针旋转rad度 33 34 double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; } //向量点乘 35 double Length(Vector A) { return sqrt(Dot(A, A)); } //向量长度 36 37 Point Up(Point A, Point B) { 38 Vector v = B - A; 39 double L = Length(v), rad = acos(L / 4); 40 Vector u = Rotate(v, rad); 41 return A + u*(2 / L); 42 } 43 44 int main() { 45 int n; 46 Point P[N][N]; 47 while (cin >> n && n) { 48 for (int i = 0; i < n; ++i) 49 scanf("%lf", &P[0][i].x), P[0][i].y = 1; 50 sort(P[0], P[0] + n); 51 for (int i = 1; i < n; ++i) 52 for (int j = 0; j < n - i; ++j) 53 P[i][j] = Up(P[i - 1][j], P[i - 1][j + 1]); 54 printf("%.4lf %.4lf\n", P[n - 1][0].x, P[n - 1][0].y); 55 } 56 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号