POJ1039 Pipe(直线交点、判断直线与线段相交)
题目链接:
http://poj.org/problem?id=1039
题目描述:
Pipe
Description
The GX Light Pipeline Company started to prepare bent pipes for the new transgalactic light pipeline. During the design phase of the new pipe shape the company ran into the problem of determining how far the light can reach inside each component of the pipe. Note that the material which the pipe is made from is not transparent and not light reflecting.
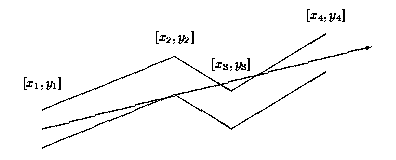
Each pipe component consists of many straight pipes connected tightly together. For the programming purposes, the company developed the description of each component as a sequence of points [x1; y1], [x2; y2], . . ., [xn; yn], where x1 < x2 < . . . xn . These are the upper points of the pipe contour. The bottom points of the pipe contour consist of points with y-coordinate decreased by 1. To each upper point [xi; yi] there is a corresponding bottom point [xi; (yi)-1] (see picture above). The company wants to find, for each pipe component, the point with maximal x-coordinate that the light will reach. The light is emitted by a segment source with endpoints [x1; (y1)-1] and [x1; y1] (endpoints are emitting light too). Assume that the light is not bent at the pipe bent points and the bent points do not stop the light beam.

Each pipe component consists of many straight pipes connected tightly together. For the programming purposes, the company developed the description of each component as a sequence of points [x1; y1], [x2; y2], . . ., [xn; yn], where x1 < x2 < . . . xn . These are the upper points of the pipe contour. The bottom points of the pipe contour consist of points with y-coordinate decreased by 1. To each upper point [xi; yi] there is a corresponding bottom point [xi; (yi)-1] (see picture above). The company wants to find, for each pipe component, the point with maximal x-coordinate that the light will reach. The light is emitted by a segment source with endpoints [x1; (y1)-1] and [x1; y1] (endpoints are emitting light too). Assume that the light is not bent at the pipe bent points and the bent points do not stop the light beam.
Input
The input file contains several blocks each describing one pipe component. Each block starts with the number of bent points 2 <= n <= 20 on separate line. Each of the next n lines contains a pair of real values xi, yi separated by space. The last block is denoted with n = 0.
Output
The output file contains lines corresponding to blocks in input file. To each block in the input file there is one line in the output file. Each such line contains either a real value, written with precision of two decimal places, or the message Through all the pipe.. The real value is the desired maximal x-coordinate of the point where the light can reach from the source for corresponding pipe component. If this value equals to xn, then the message Through all the pipe. will appear in the output file.
Sample Input
4 0 1 2 2 4 1 6 4 6 0 1 2 -0.6 5 -4.45 7 -5.57 12 -10.8 17 -16.55 0
Sample Output
4.67 Through all the pipe.
题目大意:
给一根曲曲折折的管子,判断是否存在一道光穿透管子,若不能,求最远交点横坐标
思路:
以不属于同一线段的线段端点两两组成直线
依次判断直线在每个拐点的纵坐标值是否在上下两个拐点之间
注意判断时用dcmp处理精度
代码:
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #include <cmath> 6 using namespace std; 7 8 const double EPS = 1e-10; //精度系数 9 const double PI = acos(-1.0); //π 10 const int INF = 0x3f3f3f3f; 11 const int N = 23; 12 13 struct Point { 14 double x, y; 15 Point(double x = 0, double y = 0) :x(x), y(y) {} 16 const bool operator < (Point A)const { 17 return x == A.x ? y < A.y : x < A.x; 18 } 19 }; //点的定义 20 21 typedef Point Vector; //向量的定义 22 23 Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); } //向量加法 24 Vector operator - (Vector A, Vector B) { return Vector(A.x - B.x, A.y - B.y); } //向量减法 25 Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); } //向量数乘 26 27 int dcmp(double x) { 28 if (fabs(x) < EPS)return 0; else return x < 0 ? -1 : 1; 29 } //与0的关系 30 31 double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; } //向量点乘 32 double Length(Vector A) { return sqrt(Dot(A, A)); } //向量长度 33 double Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x; } //向量叉乘 34 35 Point LineIntersectionPoint(Point A1, Point B1, Point A2, Point B2) { 36 double t1 = ((A1.y - A2.y)*(B2.x - A2.x) - (A1.x - A2.x)*(B2.y - A2.y)) / 37 ((B1.x - A1.x)*(B2.y - A2.y) - (B1.y - A1.y)*(B2.x - A2.x)); 38 return A1 + (B1 - A1)*t1; 39 } //返回直线交点 40 41 double LineInterY_axisPoint(double x, Point p, Vector v) { 42 double t = (x - p.x) / v.x; 43 return p.y + t*v.y; 44 } //直线与x=x交点纵坐标 45 46 bool SegmentIntersectWithLine(Point& a1, Point& a2, Point& st, Vector v) { 47 double c1 = Cross(a1 - st, v), c2 = Cross(a2 - st, v); 48 return dcmp(c1)*dcmp(c2) < 0; 49 } //判断线段是否与直线相交(不含端点) 50 51 double ans; 52 53 bool ok(int n, Point P[][2], Point p, Vector v) { 54 for (int i = 0; i < n; ++i) { //枚举管子折点横坐标 55 double y = LineInterY_axisPoint(P[i][0].x, p, v); 56 if (dcmp(y - P[i][0].y) > 0 || dcmp(y - P[i][1].y) < 0) { //如果位于上下点纵坐标之外 57 if (i) 58 for (int j = 0; j < 2; ++j) 59 if (SegmentIntersectWithLine(P[i - 1][j], P[i][j], p, v)) { 60 Point tmp = LineIntersectionPoint(P[i - 1][j], P[i][j], p, p + v); 61 ans = max(ans, tmp.x); 62 } 63 return false; 64 } 65 } 66 return true; 67 } 68 69 bool solve(int n, Point P[][2]) { 70 for (int i = 0; i < n - 1; ++i) 71 for (int j = i + 1; j < n; ++j) 72 for (int k = 0; k < 2; ++k) { //枚举直线 73 Point p = P[i][k]; 74 Vector v = P[j][(1 + k) % 2] - p; 75 if (ok(n, P, p, v))return true; 76 } 77 return false; 78 } 79 80 int main() { 81 int n; 82 Point P[N][2]; 83 while (cin >> n && n) { 84 ans = -INF; 85 for (int i = 0; i < n; ++i) { 86 scanf("%lf%lf", &P[i][0].x, &P[i][0].y); 87 P[i][1].x = P[i][0].x, P[i][1].y = P[i][0].y - 1; 88 } 89 if (solve(n, P))printf("Through all the pipe.\n"); 90 else printf("%.2lf\n", ans); 91 } 92 }
Pipe
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 10871 | Accepted: 3383 |
Description
The GX Light Pipeline Company started to prepare bent pipes for the new transgalactic light pipeline. During the design phase of the new pipe shape the company ran into the problem of determining how far the light can reach inside each component of the pipe. Note that the material which the pipe is made from is not transparent and not light reflecting.

Each pipe component consists of many straight pipes connected tightly together. For the programming purposes, the company developed the description of each component as a sequence of points [x1; y1], [x2; y2], . . ., [xn; yn], where x1 < x2 < . . . xn . These are the upper points of the pipe contour. The bottom points of the pipe contour consist of points with y-coordinate decreased by 1. To each upper point [xi; yi] there is a corresponding bottom point [xi; (yi)-1] (see picture above). The company wants to find, for each pipe component, the point with maximal x-coordinate that the light will reach. The light is emitted by a segment source with endpoints [x1; (y1)-1] and [x1; y1] (endpoints are emitting light too). Assume that the light is not bent at the pipe bent points and the bent points do not stop the light beam.

Each pipe component consists of many straight pipes connected tightly together. For the programming purposes, the company developed the description of each component as a sequence of points [x1; y1], [x2; y2], . . ., [xn; yn], where x1 < x2 < . . . xn . These are the upper points of the pipe contour. The bottom points of the pipe contour consist of points with y-coordinate decreased by 1. To each upper point [xi; yi] there is a corresponding bottom point [xi; (yi)-1] (see picture above). The company wants to find, for each pipe component, the point with maximal x-coordinate that the light will reach. The light is emitted by a segment source with endpoints [x1; (y1)-1] and [x1; y1] (endpoints are emitting light too). Assume that the light is not bent at the pipe bent points and the bent points do not stop the light beam.
Input
The input file contains several blocks each describing one pipe component. Each block starts with the number of bent points 2 <= n <= 20 on separate line. Each of the next n lines contains a pair of real values xi, yi separated by space. The last block is denoted with n = 0.
Output
The output file contains lines corresponding to blocks in input file. To each block in the input file there is one line in the output file. Each such line contains either a real value, written with precision of two decimal places, or the message Through all the pipe.. The real value is the desired maximal x-coordinate of the point where the light can reach from the source for corresponding pipe component. If this value equals to xn, then the message Through all the pipe. will appear in the output file.
Sample Input
4 0 1 2 2 4 1 6 4 6 0 1 2 -0.6 5 -4.45 7 -5.57 12 -10.8 17 -16.55 0
Sample Output
4.67 Through all the pipe.



